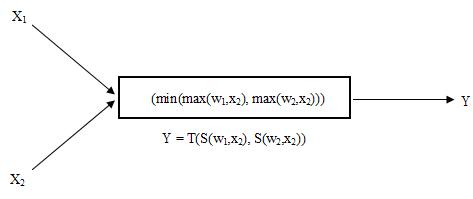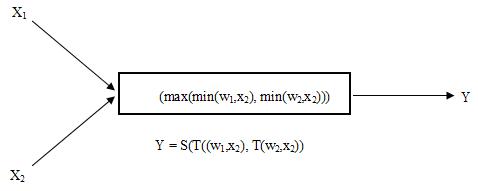Построение модели гибридных системы для обработки данных

В литературе [6,8,10] говорится, что нейронные сети хороши для распознавания образов, но весьма неудобны для выяснения вопросов, как они такое распознавание осуществляют. Они могут автоматически приобретать знания, но процесс их обучения весьма сложен и медленен.

Системы с нечеткой логикой напротив, хороши для объяснения полученного результата, но они не могут автоматически приобретать знания для использования их в механизмах вывода. Если рассматривать теоретические системы с нечеткой логикой и искусственные нейронные сети, то можно прийти к выводу, что они эквивалентны друг другу. Это соображение и легло в основу аппарата гибридных сетей. В гибридных сетях выводы делаются с помощью нечеткой логики, а функции принадлежности подстраиваются с использованием алгоритмов обучения нейронных сетей.

Цель лекции: Ознакомиться с основными понятиями гибридной системы (ГС) – как соединение нечеткой логики и нейронных сетей. Применение таких систем для моделирования и обработки данных.

Нейрокомпьютерные сети позволяют эффективно использовать аппарат, определяющий их аппроксимирующую способность. С помощью нейронных сетей можно выразить любую непрерывную функциональную зависимость, без предварительной аналитической работы по выявлению правил зависимость выхода от входа. Недостатком является невозможность объяснить выходной результат, так как значения нейронов определены в виде коэффициентов весов.

В связи с этим применение нечетких систем оправдано. Ассоциативному мышлению адекватны логические нейронные сети, создаваемые на основе логического описания системы управления или принятия решений в терминах алгебры высказываний. Если система принятия решений функционально полностью определена и может быть описана в терминах математической логики, то по этому описанию целесообразно строить нейронную сеть. С помощью логических построений легко построить объяснение результата в форме протокола рассуждений. Поэтому гибридные системы наиболее интересны в вопросах исследования. Они сочетают в себе преимущества нечетких систем и нейронных сетей. [6]

Примером таких технологий служит реализация системы нечетких правил на основе нейросети. Набор нечетких правил для двух входных и одной выходной переменных имеет следующую структуру (14.1):

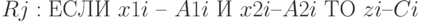( 14.1)

Рис. 14.1. Представление функции принадлежности α – срезами

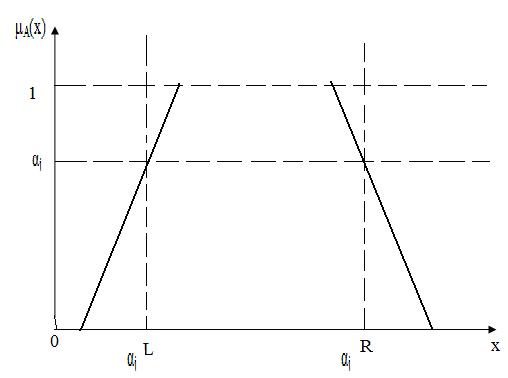
Один из способов представления нечеткого понятия в виде четких данных состоит в представлении нечеткого множества в виде α – срезов (см. Рисунок 14.2). При этом использовании α – срезов представляется в виде подмножеств α _j, где j – номер среза с двумя границами L и R, т.е. α – срезы четко представляют непрерывную функцию принадлежности.

Функция модели нейрона в гибридной сети отличается от функции традиционного нейрона.

Модификация модели нейрона для адаптации к нечетким системам касается выбора функции активации, реализации операции сложения и умножения, так как в нечеткой логике сложение моделируется любой треугольной к нормой, а операция умножения – треугольной нормой.

И – нейроном называется нейрон, в котором умножение веса w на вход x моделируется S(w,x), а сложение T(w,x) (см. Рисунок 14.2)

Рис. 14.2. Двухвходовый И – нейрон

ИЛИ – нейроном называется нейрон, в котором умножение веса w и входа x моделируются нормой T(w,x) а сложение взвешенных весов к нормой S(w,x) если выбрать в качестве Т min, а S max формула преобразуется и будет (max(min(w1,x2), min(w2,x2))) (см. Рисунок 14.3)

Рис. 14.3. Двухвходовой ИЛИ – нейрон

В качестве функции активации обычно используют радиальную базисную функцию

( 14.2)

Нечеткой нейронной сетью (ННС) называют четкую нейронную сеть прямого распространения сигнала, которая построена на основе многослойной архитектуры с использованием И – , ИЛИ – нейронов.

Нечеткая нейронная сеть функционирует стандартным образом на основе четких действительных чисел, нечеткой является интерпретация результатов. При создании гибридной технологии используются настройки параметров функции принадлежности.

Традиционно функции принадлежности формируются двумя способами с помощью статистических или экспериментальных данных. При создании гибридной системы предлагается использовать метод выбора в качестве функции принадлежности параметризированную функцию формы, параметры которой настраиваются с помощью нейронных сетей. Настройка параметров может быть получена с помощью алгоритма обратного распространения ошибки.

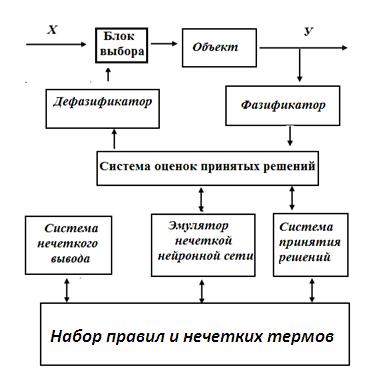
Для работы такой сети необходима система. Можно выделить два основной принцип работы данной системы, это отказ от точных цифр в пользу нечетких, но содержательных оценок, которые позволяют принять осмысленное решение. Если рассматривать деятельность данной системы как управление объектом, то инструментарий экспертизы можно использовать, как управление объектом. И представить ее в виде структуры схемы системы для построения нейронной сети (см. Рисунок 14.4). Система извлекает знания из статических выборок, интерпретируя их как обучающие выборки для обучения нейронной сети.

Рис. 14.4. Структурная схема гибридной системы