НОУ ИНТУИТ | Обработка экспериментальных данных. Лекция 6: Применение теории нечетких множеств для обработки данных

Учитесь и получайте официальные документы БЕСПЛАТНО. Вы можете поддержать наш проект.

Твой путь к знаниям!

Опубликован: 13.08.2013 | Уровень: для всех | Доступ: платный | ВУЗ: Поволжский Государственный Университет Телекоммуникаций и Информатики

|

Вам нравится? Нравится 47 студентам

| Поделиться |

Поддержать программу

Пусть А, В, С - нечеткие множества, тогда выполняются следующие свойства:

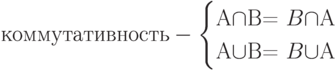$коммутативность - \begin{cases} $A\cap$B= $B\cap$A\\ $A\cup$B= $B\cup$A \end{cases}$

( 12.5)

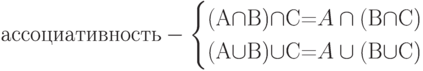$ассоциативность - \begin{cases} ($A\cap$B)\cap$C=$A\cap($B\cap$C)\\ ($A\cup$B)\cup$C=$A\cup($B\cup$C) \end{cases}$

( 12.6)

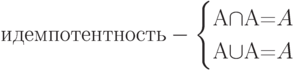$идемпотентность - \begin{cases} $A\cap$A=$A\\ $A\cup$A=$A \end{cases}$

( 12.7)

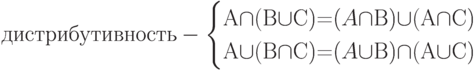$дистрибутивность - \begin{cases} $A\cap($B\cup$C)=($A\cap$B)\cup($A\cap$C)\\ $A\cup($B\cap$C)=($A\cup$B)\cap($A\cup$C) \end{cases}$

( 12.8)

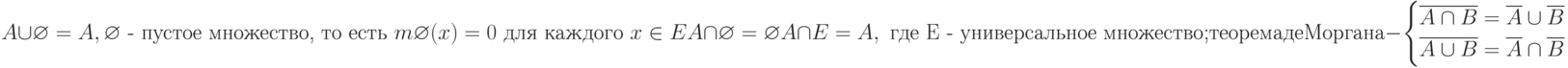$A\cup\varnothing=A, \varnothing\text{ - пустое множество, то есть }m\varnothing(x)=0\text{ для каждого }x \in E\\ A\cap\varnothing=\varnothing\\ A\cap E=A, \text{ где E - универсальное множество;}\\ теорема де Моргана - \begin{cases} \overline{A\cap B}=\overline{A}\cup\overline {B}\\ \overline{A\cup B}=\overline{A}\cap\overline {B} \end{cases}$

( 12.9)

В отличие от четких множеств, для нечетких множеств в общем случае:

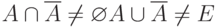$A \cap\overline A\neq\varnothing\\ A\cup \overline A \neq E$

( 12.10)

(Что, в частности, проиллюстрировано выше в примере представления нечетких множеств).

$CON(A) = A2 \text{- операция концентрирования}, \\ DIL(A) = A0,5 \text{- операция размывания}$

Все это операции нечетких множеств, которые используются при работе с лингвистическими переменными [7,9,22].

Рис. 12.7. Нечеткие множества

При описании объектов и явлений с помощью нечетких множеств используется понятие нечеткой и лингвистической переменных [21].

Нечеткая переменная характеризуется тройкой 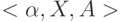$< \alpha, X, A >$ , где

$\alpha$ - имя переменной,

- универсальное множество (область определения $\alpha$

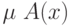- нечеткое множество на , описывающее ограничение (то есть $\mu \text{ }A(x)$ ) на значение нечеткой переменной $\alpha$ .

Лингвистической переменной называется набор 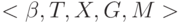$< \beta, T,X,G,M >$ , где

$\beta$ - имя лингвистической переменной;

- множество его значений (терм-множество), представляющие имена нечетких переменных, областью определения, которых является множество . Множество называется базовым терм - множеством лингвистической переменной;

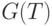- синтаксическая процедура, позволяющая оперировать элементами терм - множества , в частности, генерировать новые термы (значения). Множество $T \cap G(T)$ , где G(T) - множество сгенерированных термов, называется расширенным терм - множеством лингвистической переменной;

- семантическая процедура, позволяющая преобразовать новое значение лингвистической переменной, образованной процедурой , в нечеткую переменную, то есть сформировать соответствующее нечеткое множество [7].

Пример применения нечеткого множества для нахождения оптимального маршрута передачи данных по сети.

Создадим модель, ориентированную на решение задачи "проникновения" из пункта отправления в пункт назначения кратчайшим или менее загруженным доступным путем, т.е. за минимально возможное время.

Разработаем правила, которые задают связь входных переменных с выходными.

Для лингвистической оценки входных и выходных переменных используем следующие терм множества:

х1 – максимальное количество переходов (K=4); среднее количество переходов (КС); минимальное количество переходов (МК=1);
х2 – скорость передачи информации по сети максимальная (Т=5,4 мбит/с.), скорость передачи информации по сети средняя (ТС), минимальная скорость передачи информации (МТ=1,8 мбит/с);
у – максимальное время прохождения пакета (G=1,84сек), среднее время прохождения пакета (GС), минимальное время прохождения пакета (MG=0,1сек).

Сведем все значения в таблицу 12.1.

Таблица 12.1. Комбинации термов
№	x1	x2	y
1	K	MT	G
2	KC	T	MG
3	KC	TC	GC
4	MK	T	MG

Применим систему типа Сугэно. Если значение выходной переменной в правиле задано нечетким множеством, тогда правило может быть представлено нечетким отношением. Для нечеткого правила, если значение выходной переменной в правиле задано нечетким множеством, тогда правило может быть представлено нечетким отношением. 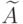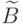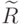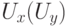Для нечеткого правила "Если x есть $\widetilde A$ , то y есть $\widetilde B$ нечеткое отношение $\widetilde R$ задается на декартовом произведении $U_x \times U_y$ , где U_x(U_y) - универсальное множество входной (выходной) переменной. [6] Для расчета нечеткого отношения можно применять нечеткую импликацию и t-норму. При использовании в качестве t-нормы операции нахождения минимума, расчет нечеткого отношения 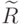$\widetilde R$ осуществляется так [5]:

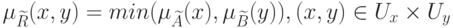$\mu_{\widetilde R}(x,y)=min(\mu_{\widetilde A}(x),\mu_{\widetilde B}(y)), (x,y) \in U_x \times U_y$

( 12.11)

Согласно этому утверждению разработаем правила, которые будут применяться на основных этапах проектирования систем типа Сугэно на примере создания системы нечеткого логического вывода, моделирующей зависимость.

Если х1= К и х2=МТ, то у=1,84;
Если х1=КС и х2=ТС, то у=1,47;
Если х1=КС и х2=ТС, то у=0,37;
Если х1=МК и х2=Т, то у=0,1;

Дальше >>

Обработка экспериментальных данных

Обработка экспериментальных данных

Применение теории нечетких множеств для обработки данных

Вопросы и ответы

Студенты

Авторизоваться

Обработка экспериментальных данных

Обработка экспериментальных данных

Применение теории нечетких множеств для обработки данных

Вопросы и ответы

Студенты