| Россия |
Применение теории нечетких множеств для обработки данных
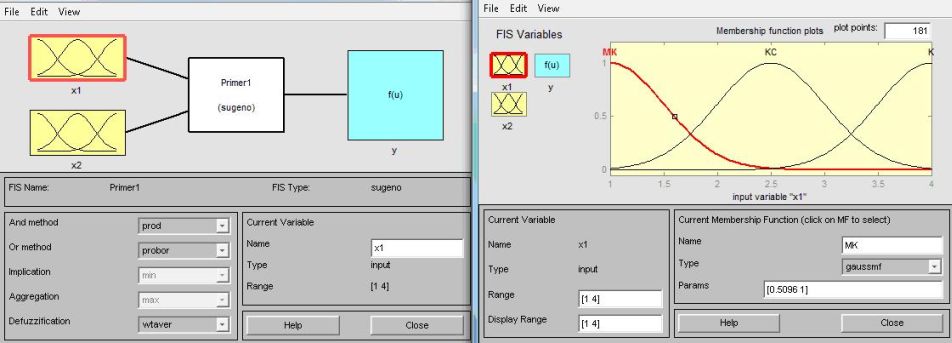
Проектирование системы нечеткого логического вывода типа Сугэно состоит в выполнении следующей последовательности шагов. Сначала вводим входные переменные 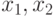 и выходную
и выходную  . Обозначим термы и введем диапазон изменения переменных согласно выведенным правилам. Каждому терму будет соответствовать три переменные на входе это
. Обозначим термы и введем диапазон изменения переменных согласно выведенным правилам. Каждому терму будет соответствовать три переменные на входе это  на выходе
на выходе 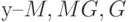 . Тип функции выберем gaussmf
. Тип функции выберем gaussmf 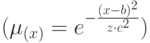 симметричная гауссовская функция принадлежности) [25]. Количество точек дискретизации для построения функции принадлежности возьмем равное 181 (Рисунок 12.8).
симметричная гауссовская функция принадлежности) [25]. Количество точек дискретизации для построения функции принадлежности возьмем равное 181 (Рисунок 12.8).
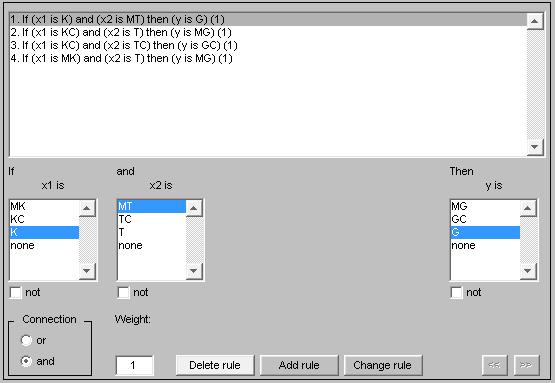
На следующем этапе прописываются правила (соответствующие комбинации термов, указанные в таблице 12.1) которые необходимы для нахождения необходимого маршрута передачи данных ( рис. 12.9). Согласно этим правилам строится модель нечеткой системы.
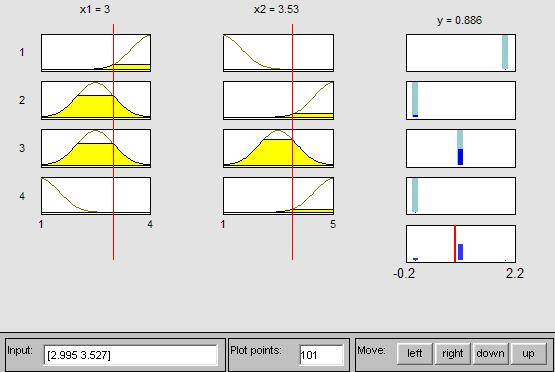
Результат моделирования отображается в графическом окне. Входной вектор в каждом из этих вариантов определения исходных данных, задается набором вертикальных линий (см. рис. 12.10)
Построенная модель прохождения пакетов позволяет сделать выбор маршрута быстро без лишних расчетов, учитывая необходимую стратегию маршрутизации.
В данном случае х1 =3 – это количество переходов, х2 =3,5 Мбит/с – скорость передачи информации, у=0,8 сек – время которое будет затрачено на прохождение по данному маршруту, все это отображено в окне.
В MATLAB имеется встроенный пакет расширения fuzzy, в котором есть компонент моделирования системы Сугэно в виде поверхностей "входов" и "выходов" синтезированной нечеткой системы.
Меню X (input), Y (input), Z (output) позволяют поставить в соответствие осям координат входные и выходные переменные.
Данное средство просмотра правил вывода позволяет наглядно отобразить сам процесс маршрутизации и быстро получить результат поиска, не применяя сложных расчетов.
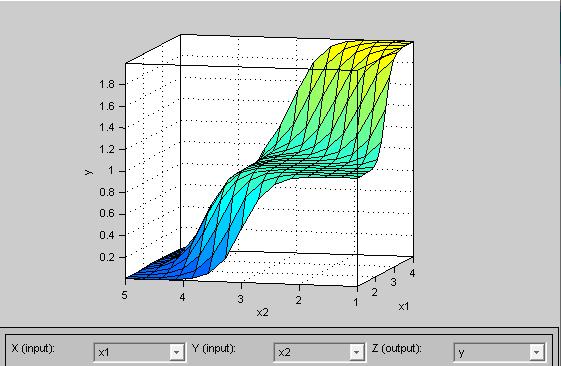
Рис. 12.11. Поверхность «входы» и «выходы» для системы Сугэно, определяющие выбор маршрута в сети в зависимости от входных параметров
На рис. 12.11 показана зависимость у (время прохождения пакета по сети) от х1 (количества переходов) и х2 (скорость передачи информации). Значения у соответственно меняются в зависимости от задаваемых входных переменных.
Приведенный пример показывает насколько просто и эффективно можно применить нечеткую логику для обработки экспериментальных данных.
Краткие итоги
В лекции были рассмотрены основные понятия нечеткого множества. Отличия нечеткого подмножества от обычного. Оно отличается тем, что для элементов x из E нет однозначного ответа "нет" относительно свойства R.
Графическое изображение нечеткого подмножества. Приведен пример использования нечеткой логики для обработки данных с применением программы MATLAB. Эта программа имеется встроенный пакет расширения fuzzy, в котором есть компонент моделирования системы Сугэно в виде поверхностей "входов" и "выходов" синтезированной нечеткой системы.
Вопросы для самопроверки
- Что называют нечетким подмножеством?
- Чем отличается нечеткое множество от обычного?
- Как записываются операции объединения и пересечения для нечеткого множества?
- Какой функцией характеризуется нечеткое подмножество А множества Х?
- Что указывает функция принадлежности?
- При каком условии нечеткое множество A является нормальным?
- Перечислите какие свойства выполняются если А, В, С - нечеткие множества?
- Что называют терм-множеством?