Сжатие изображений с потерями
14.6. Фрактальное сжатие
Фрактальное сжатие основывается на поиске и кодировании самоподобных областей в изображении. При этом используются системы итерируемых функций (англ. IFS - Iterated Function System) [31], [12].
Определение 14.6.1. Отображение  в полном метрическом пространстве
в полном метрическом пространстве 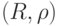 называется сжимающим, если
называется сжимающим, если 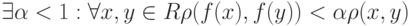 .
.
Cистеме из  сжимающих отображений
сжимающих отображений 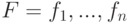 , действующих в полном метрическом пространстве
, действующих в полном метрическом пространстве 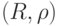 , ставится в соответствие оператор системы итерируемых функций
, ставится в соответствие оператор системы итерируемых функций

где 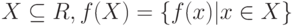 . Такое отображение является сжимающим с коэффициентом
. Такое отображение является сжимающим с коэффициентом

По теореме о сжимающих отображениях [3] существует неподвижное множество  .
.
Рассмотрим пример действия системы итерируемых функций. Пусть
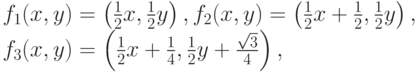
действуют в пространстве R = [0; 1]2 с евклидовой метрикой. Данные отображения являются сжимающими 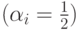 , и их неподвижные точки есть вершины равностороннего треугольника (их координаты
, и их неподвижные точки есть вершины равностороннего треугольника (их координаты 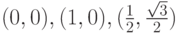 соответственно). Сначала будем последовательно применять оператор F* данных преобразований к множеству, ограниченному равносторонним треугольником
(например, с координатами вершин, указанными выше). Неподвижное множество S, получаемое при действии оператора данной системы итерируемых функций, - это так называемый треугольник Серпинского (см. рис. 14.7). Процесс построения треугольника Серпинского см. на рис. 14.8. Можно начать применять оператор данных преобразований не к треугольнику, а к квадрату. Неподвижное множество будет таким же (см. рис. 14.9). Неважно, с какой области начинать (требуется только компактность), - получим треугольник Серпинского.
соответственно). Сначала будем последовательно применять оператор F* данных преобразований к множеству, ограниченному равносторонним треугольником
(например, с координатами вершин, указанными выше). Неподвижное множество S, получаемое при действии оператора данной системы итерируемых функций, - это так называемый треугольник Серпинского (см. рис. 14.7). Процесс построения треугольника Серпинского см. на рис. 14.8. Можно начать применять оператор данных преобразований не к треугольнику, а к квадрату. Неподвижное множество будет таким же (см. рис. 14.9). Неважно, с какой области начинать (требуется только компактность), - получим треугольник Серпинского.
Другим примером неподвижного множества S для оператора F* для некоторой системы F из четырех аффинных преобразований является папоротник Барнсли (см. рис. 14.10).
Изображение папоротника может занимать десятки мегабайт (в хорошем разрешении), а его описание с помощью параметров аффинных преобразования - несколько сотен байт! Соответственно, идея сжатия состоит в поиске таких систем преобразований, которые бы в процессе итерирования приближали желаемое изображение. Задача ставится так:
Сложность такой задачи в общем случае очень высока. Однако, если рассматривать изображение как функцию (см. введение "Сжатие изображений с потерями" ) и ограничивать вид преобразований следующим образом:
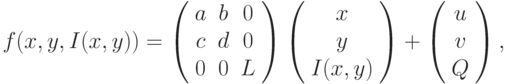
т.е. аффинными преобразованиями, то задача упрощается. Тем не менее время работы, требуемое для поиска коэффициентов преобразования, слишком велико. Для ускорения алгоритма поиска коэффициентов налагаются специальные ограничения на вид и размер множеств, к которым применяются преобразования, а также на сам вид преобразований, т.е. фиксированное множество углов поворота и коэффициентов масштабирования. Таким образом, задача становится дискретной и возможен прямой подбор параметров.
В реальной жизни изображения, подобные папоротнику Барнсли (т.е. состоящие только из самоподобий), встречаются редко, поэтому ожидать похожей степени сжатия нельзя. Тем не менее качество восстановленных изображений при высоких степенях сжатия значительно превосходит JPEG. К недостаткам алгоритма относят очень долгое время сжатия по сравнению с другими методами, а также наличие патентов.




