Сжатие изображений с потерями
14.5. Вейвлет-преобразование
Идея вейвлет-преобразования состоит в разложении сигнала (функции-изображения) по системе функций, имеющих локальный всплеск и быстро убывающих на бесконечности [20]. В этом и последующих параграфах предполагается знакомство читателя с базовыми понятиями функционального анализа (см., например, [3]). Обычно такие функции вейвлет-преобразования2от англ. wavelet transform выводятся из так называемого материнского вейвлета. Материнский вейвлет - это функция 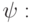
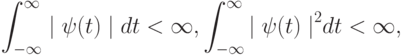
т.е.  ; также предполагается, что
; также предполагается, что

Материнский вейвлет преобразовывается следующим образом:
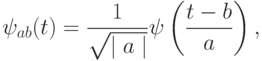
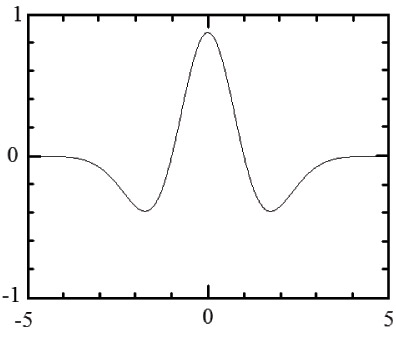
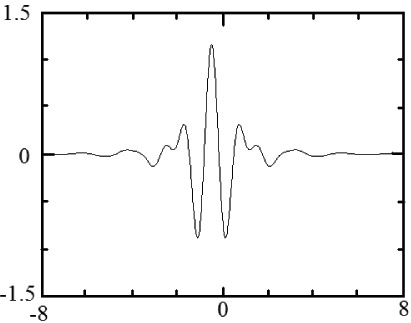
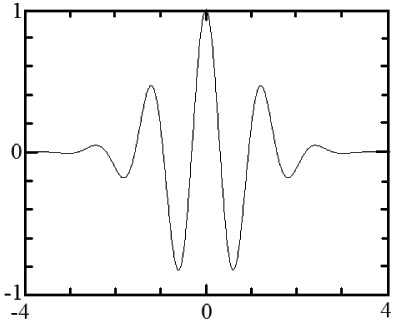
где 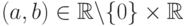 . Примеры материнских вейвлетов см. на рис. 14.5. В общем случае вейвлет-преобразование записывается так:
. Примеры материнских вейвлетов см. на рис. 14.5. В общем случае вейвлет-преобразование записывается так:
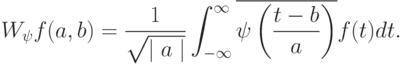
При практическом применении вейвлет-преобразования анализ такого мощного (а именно континуум) множества коэффициентов невозможен. Поэтому (a, b) выбираются из счетного подмножества плоскости 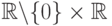 . Обычно материнский вейвлет и множество значений (a, b) выбирают так, чтобы система
. Обычно материнский вейвлет и множество значений (a, b) выбирают так, чтобы система 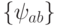 образовывала ортонормированный базис в пространстве
образовывала ортонормированный базис в пространстве 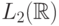 . Тогда любую функцию f(x) из этого пространства можно разложить по этому базису
. Тогда любую функцию f(x) из этого пространства можно разложить по этому базису 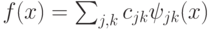 .
.
Поясним как применять вейвлет-преобразование к дискретному сигналу (например, изображению). Для простоты будем рассматривать одномерный случай - последовательность конечной длины  . Тогда, при условии что материнский вейвлет
. Тогда, при условии что материнский вейвлет 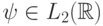 , преобразование можно записать так:
, преобразование можно записать так:
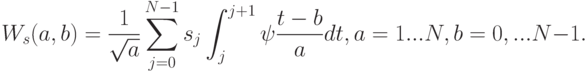
Рассмотрим простейшей вейвлет - вейвлет Хаара (англ. Haar wavelet). Рассмотрим пространство 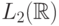 . В этом пространстве ортонормированна следующая система:
. В этом пространстве ортонормированна следующая система:
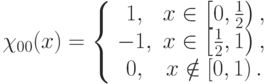
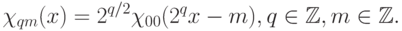
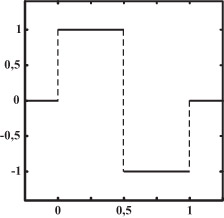
Данная система называется системой Хаара. Для такого вейвлета материнским является 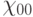 (см. рис. 14.6). В данном случае (a, b) выбраны из
(см. рис. 14.6). В данном случае (a, b) выбраны из  по такому закону:
по такому закону:
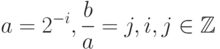
Действие вейвлета Хаара на последовательность, состоящую из 2N элементов, можно рассматривать так: элементы группируются по два, вычисляется сумма и разность каждой пары, разности сохраняются, а из сумм формируется последовательность длины 2N-1 ; далее преобразование выполняется до тех пор, пока не останется одна сумма и соответственно 2N - 1 разность. Такое преобразование задается так называемой матрицей Хаара:
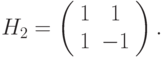
Последовательность (a0, . . . , a2N+1) представим так:
((a0, a1), . . . , (a2N, a2N+1)).
Теперь умножим справа векторы (ai, ai+1) на матрицу H2. Получим последовательность сумм и разностей ((s0, d0), . . . , (sN, dN)). Если последовательность имеет длину, кратную 4, то можно применить следующую матрицу Хаара:

Очевидно, что данные преобразования легко обратимы. С таким вейвлет-преобразованием тесно связано так называемое S-преобразование. Если мы не хотим, чтобы при преобразовании Хаара границы значений последовательности удваивались (из-за суммирования), надо брать полусумму. Однако при целом делении на 2 мы теряем точность. Решение данной проблемы выглядит так: пусть a и b - пара значений из исходной последовательности. Тогда
![s = \left[\frac{a + b}{2}\right], d = a - b,](/sites/default/files/tex_cache/2730cf5b2ddfb341d84baa75287b3e88.png)
при этом восстановление выглядит так:
![a = s + \left[\frac{d}{2}\right], b = s - \left[\frac{d}{2}\right],](/sites/default/files/tex_cache/f346f0d5a0f75c3adaf1a2bb1cf8b69b.png)
при этом, если d - нечетное, то при d > 0 к a добавляется 1, а если d < 0, то к b добавляется 1.
// s - сумма, d - разность
// Round(x) - взятие целой части
// IsOdd(x) - является ли нечетным
a = s + Round( d / 2 ); b = s - Round( d / 2 )
if( IsOdd( d ) )
{
if ( d > 0 )
a++;
else
b++;
}
Листинг
14.1.
Алгоритм
В алгоритме JPEG2000 [10] используются так называемые вейвлеты Добеши (англ. Daubechies wavelet). В матричном виде для действия на вектор A длины 8 данное преобразование задается так:
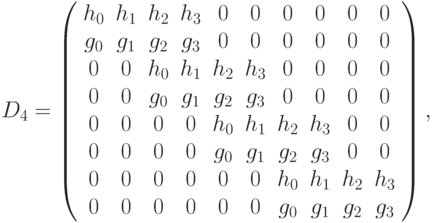
где
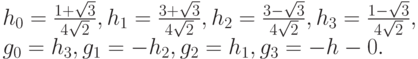
Как видно, матрица имеет размеры 8 x 10 из-за необходимости участия в суммировании четырех компонент. Т.е. на самом деле, такая матрица умножается на следующий вектор:
A = (a1a2a3a4a5a6a7a8a9a10)T .
Обычно полагают либо a9 = a1, a10 = a2, либо a9 = a8, a10 = a7. Использование вейвлет-преобразований при сжатии изображений аналогично использованию дискретного косинус-преобразования в алгоритме JPEG, т.е. само преобразование - лишь ступень конвейера сжатия.
Вейвлет-преобразования имеют очень хорошую частотно-пространственную локализацию и по этому показателю превосходят традиционные косинус-преобразования и другие преобразования Фурье. Таким образом, становится возможно применять более сильное квантование, улучшая свойства последовательности для последующего сжатия без потерь. Алгоритмы сжатия изображений, основанные на этом преобразовании, при той же степени сжатия показывают лучшие результаты по сохранению качества изображения. К тому же вычислительная сложность очень низка и составляет O(N) (здесь N - длина последовательности, к которой применяется преобразование). Однако распространенность форматов, использующих сжатие на основе вейвлет-преобразования, невелика из-за наличия патентов, а также из-за большой распространенности обычного JPEG, дающего вполне приемлемые результаты.