|
Здравствуйте. А уточните, пожалуйста, по какой причине стоимость изменилась? Была стоимость в 1 рубль, стала в 9900 рублей. |
Приложение А
Упражнение 12.19. Система организации очереди М/М/3
Мы рассматриваем классическую систему организации очереди Эрланга 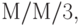 имеющую 3 обслуживающих прибора и неограниченное число мест ожидания в очереди. Заявки от клиентов поступают согласно Пуассоновскому процессу с интенсивностью
имеющую 3 обслуживающих прибора и неограниченное число мест ожидания в очереди. Заявки от клиентов поступают согласно Пуассоновскому процессу с интенсивностью  в единицу времени клиентов, а время обслуживания экспоненциально распределено с интенсивностью . Состояние системы определено как общее количество клиентов в системе.
в единицу времени клиентов, а время обслуживания экспоненциально распределено с интенсивностью . Состояние системы определено как общее количество клиентов в системе.
- Найти предложенную нагрузку. Выполнены ли условия статистического равновесия?
- Построить диаграмму переходов между состояниями и найти вероятности состояний, когда система находится в статистическом равновесии.
- Вычислить вероятность времени ожидания (С-формула Эрланга), используя рекурсивную формулу для В-формулы Эрланга, чтобы вычислить С-формулу. В решении должны быть использованы отдельные шаги рекурсии.
- Найти (а) среднюю длину очереди в случайный момент времени, (b) среднее время ожидания для всех клиентов, и (с) среднее время ожидания для клиентов (время ожидания > 0).
- (Расширенный вопрос) При рассмотрении примите условие, что на эти три сервера претендуют в последовательном порядке, и найдите нагрузку, которую обслуживает каждый из этих трех серверов (используйте данные, полученные при ответе на вопрос 3).
- Вывести рисунок диаграмму фазового перехода во время реакции (время обслуживания + возможное время ожидания). Найдите среднюю величину, и коэффициент формы этого времени реакции.
Упражнение 12.23. Система организации очереди М/М/1 с ограниченным доступом
Мы рассматриваем 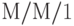 -систему организации очереди с одним обслуживающим прибором и бесконечной очередью. Клиенты прибывают согласно Пуассоновскому процессу со скоростью
-систему организации очереди с одним обслуживающим прибором и бесконечной очередью. Клиенты прибывают согласно Пуассоновскому процессу со скоростью  клиентов в единицу времени, и время обслуживания - экспоненциально распределенное со средней величиной
клиентов в единицу времени, и время обслуживания - экспоненциально распределенное со средней величиной 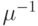 . Сервер выходит из строя со скоростью
. Сервер выходит из строя со скоростью  (в состоянии свободно) и восстанавливается с интенсивностью
(в состоянии свободно) и восстанавливается с интенсивностью  . Все временные интервалы экспоненциально распределены. Когда сервер выходит из строя, клиенты не обслуживаются. Для заявки от клиента, который находится в обслуживании, когда сервер сломался, обслуживание возобновляется, когда сервер восстановлен. Заявки от клиентов, прибывающие в течение периода ремонта, теряются.
. Все временные интервалы экспоненциально распределены. Когда сервер выходит из строя, клиенты не обслуживаются. Для заявки от клиента, который находится в обслуживании, когда сервер сломался, обслуживание возобновляется, когда сервер восстановлен. Заявки от клиентов, прибывающие в течение периода ремонта, теряются.
Состояние системы определяется как 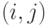 , где
, где 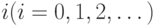 - общее количество клиентов в системе и
- общее количество клиентов в системе и  - состояние обслуживающего прибора (сервера): 0 - при обслуживании, 1 - при ремонте.
- состояние обслуживающего прибора (сервера): 0 - при обслуживании, 1 - при ремонте.
- Создать диаграмму переходов состояний системы.
- Найти соотношение времени, когда обслуживающий прибор сломан и когда обслуживающий прибор работает.
- Найти вероятности состояния системы согласно предположению о статистическом равновесии.
-
Какова вероятность (выраженная вероятностями состояний), что вызов:
- обслуживается немедленно без задержки (из-за очереди или ремонта)?
- задерживается перед обслуживанием?
- потерян?
- Какие ограничения должны быть выполнены между
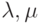 и
и  , когда система способна достигнуть статистического равновесия?
, когда система способна достигнуть статистического равновесия? -
Объяснить распределение Кокса для временного интервала от начала до завершения обслуживания клиента.
Упражнение 12.24. Модель ремонта машин Пальма и обобщенное совместное использование процессора
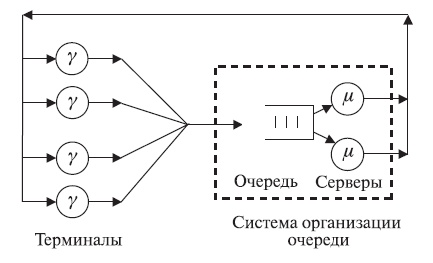
Мы рассматриваем модель ремонта машин Пальма с четырьмя терминалами и двумя серверами, работающими параллельно. Времена раздумья - экспоненциально распределенные со средней величиной 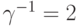 единицы времени. Времена обслуживания - экспоненциально распределенные со средней величиной
единицы времени. Времена обслуживания - экспоненциально распределенные со средней величиной 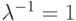 единицы времени. Состояние системы определено обычным способом как число обслуживаемых терминалов или находящихся на ожидании.
единицы времени. Состояние системы определено обычным способом как число обслуживаемых терминалов или находящихся на ожидании.
- Найти нагрузку, предлагаемую этим двум серверам.
-
Создать диаграмму переходов состояний и найти вероятности состояния
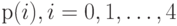 в момент статистического равновесия.
в момент статистического равновесия. -
Найти среднее число терминалов, которые находятся в состоянии:
- размышления,
- ожидания,
- обслуживания.
- Найти потери по нагрузке С.
-
Найти, применяя Теорему Литла к очереди и на оба сервера, время реакции, которое является математическим ожиданием суммы времени ожидания обслуживания + времени обслуживания.
Теперь примем, что времена обслуживания подчиняются закону гипер распределения:
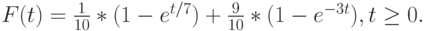
Состояние системы теперь определено как
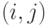 , где
, где 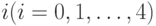 - число заявок, обслуживаемых в фазе один, и
- число заявок, обслуживаемых в фазе один, и 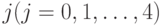 - число заявок, обслуживаемых в фазе два,
- число заявок, обслуживаемых в фазе два,  :
:Также принимаем, что два сервера работают в режиме совместного использования процессора, когда более чем два терминала находятся в очереди. Таким образом, скорость обслуживания в состоянии
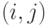 тогда
тогда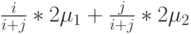
Когда два или меньше терминалов обслуживаются, каждый терминал имеет собственный сервер.
- Создать двухмерную диаграмму переходов состояний.
- Рассмотреть диаграмму переходов состояний: показать, что а) они обратимы, b} имеют мультипликативную форму.
- Показать, что соединенные вероятности состояния
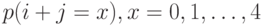 ; являются такими же, как вероятности состояния, полученные в вопросе 2.
; являются такими же, как вероятности состояния, полученные в вопросе 2.
Упражнение 13.4. Система организации очереди М/Е2/1
Мы рассматриваем систему организации очереди 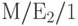 , куда прибывают вызовы с интенсивностью
, куда прибывают вызовы с интенсивностью  и временем обслуживания - распределенным в соответствии с Эрланговским распределением с интенсивностью
и временем обслуживания - распределенным в соответствии с Эрланговским распределением с интенсивностью 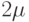 в каждой из двух фаз.
в каждой из двух фаз.
- Найти предложенную нагрузку.
- Создать диаграмму переходов состояний для системы, где состояние обозначает число клиентов в системе и фазу обслуживающего прибора.
- Найти среднее время ожидания для произвольного вызова и среднее время ожидания вызова, который поставлен на ожидание.
- Найти среднюю величину временного интервала, который проходит в случайный момент времени, пока не будет обслужен клиент с очень высоким приоритетом (дисциплина очереди - без приоритета).
- Найдите производящую функцию (или функцию распределения) и среднюю величину и дисперсию числа заявок от клиентов, которые прибывают в течение времени обслуживания.
-
Предположим, что все заявки от клиентов имеют вышеупомянутое распределение времени обслуживания, и выберем среднее время обслуживания как единицу времени. Рассмотрим систему организации очереди с двумя классами и предложенной нагрузкой, равной 0.4 Эрл на каждый класс. Один из классов имеет более высокий приоритет. Найдите среднее время ожидания для клиентов в каждом из двух классов, когда дисциплина организации очереди:
- неприоритетная,
- приоритетное возвращение к работе.
Упражнение 13.7. М/Н2/1 система организации очереди с совместным использованием процессора
Заявки прибываютв компьютерную систему согласно Пуассоновскому процессу с интенсивностью  .
.
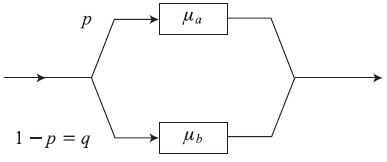
Время обслуживания имеет гиперэкспоненциальное распределение с двумя фазами, обозначенными а и соответственно b:
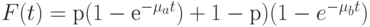
-
Найти предложенную нагрузку А.
Далее мы принимаем, что
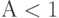 . Компьютерная система работает как система с одним обслуживающим прибором (процессор), использующим совместную дисциплину организации очереди, то есть если в системе есть
. Компьютерная система работает как система с одним обслуживающим прибором (процессор), использующим совместную дисциплину организации очереди, то есть если в системе есть  заявок, то работа в фазе а обслуживается со скоростью
заявок, то работа в фазе а обслуживается со скоростью  и работа в фазе b обслуживается со скоростью
и работа в фазе b обслуживается со скоростью 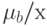 . Состояние системы определяется
. Состояние системы определяется 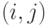 , где
, где  - число заявок в фазе a, a
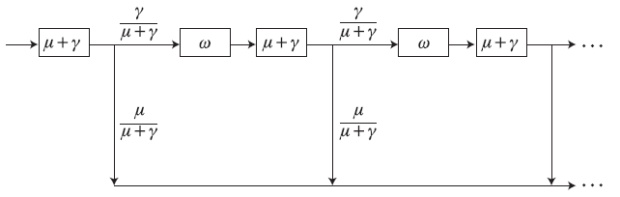
- число заявок в фазе a, a  - число вакансий в фазе b. Диаграмма переходов состояний будет двухмерной со структурой, показанной на рисунке.
- число вакансий в фазе b. Диаграмма переходов состояний будет двухмерной со структурой, показанной на рисунке. - Найти отсутствующую интенсивность в соединении с состоянием: (1,1), (1,2), (2,2) и (2,1).
-
Показать, рассматривая вышеупомянутые четыре состояния, что диаграмма переходов состояний обратима.
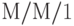 -система организации очереди с предложенной нагрузкой (при
-система организации очереди с предложенной нагрузкой (при 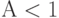 ) имеет вероятности состояния равновесия:
) имеет вероятности состояния равновесия: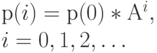
-
Показать, выражая вероятности состояния через состояние
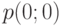 , что вышеупомянутая система
, что вышеупомянутая система  , где процессор совместно использует систему, имеет те же самые вероятности состояний, что и
, где процессор совместно использует систему, имеет те же самые вероятности состояний, что и 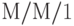 , когда мы предполагаем, что:
, когда мы предполагаем, что: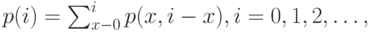
и рассматриваем только
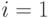 и
и  .
.
Упражнение 13.8. Циклическая система организации очереди
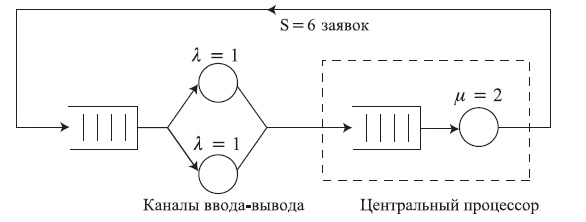
Мы рассматриваем следующую циклическую систему организации очереди.
Шесть заявок циркулируют в системе и обслуживаются альтернативно в центральном процессоре (экспоненциально распределенное время обслуживания со средней величиной 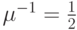 единицы времени) и в один из двух каналов ввода/вывода (полная доступность, экспоненциально распределенное время обслуживания со средней величиной
единицы времени) и в один из двух каналов ввода/вывода (полная доступность, экспоненциально распределенное время обслуживания со средней величиной 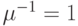 единица времени). Если оба канала ввода/вывода являются свободными, заявка выбирает канал случайным образом.
единица времени). Если оба канала ввода/вывода являются свободными, заявка выбирает канал случайным образом.
Состояние системы определяется как число заявок, которые обслуживаются или ждут в очереди в центральном процессоре (соответствует числу заявок в блоке Центральный процессор на рисунке). Предполагается, что система находится в статистическом равновесии.
- Создать диаграмму переходов состояний системы и найти вероятности состояния.
- Найти использование центрального процессора и каждого из двух каналов ввода-вывода.
-
Вычислить среднюю длину очереди в каждой из двух систем организации очереди, используя вероятности состояний. Примените формулу Литтла, чтобы получить полное время циркуляции для случайной работы. (Время циркуляции - среднее время общего количества циклов).
Вероятности состояния, полученные в вопросе 1 - математические ожидания времени, то есть вероятности состояния в случайный момент времени.
-
Найти вероятности состояния, для заявки, которая только закончила обслуживание в "канале ввода-вывода" и поступает в систему очередь - центральный процессор (математическое ожидание вызова). Затем вычислите вероятность, что заявка будет ожидать обслуживания (положительное время ожидания) в Центральном процессоре, соответственно в каналах ввода-вывода.
Найдите средние времена ожидания для задержанного вызова в центральном процессоре, соответственно в канале ввода-вывода.
- Вычислите вероятность состояния, используя алгоритм свертывания для сети очередей.
Упражнение 13.19. "Дырявое ведро": система организации очереди M/D/1/2
Основные положения
"Дырявое ведро" - механизм для управления ячейкой (пакетом) в ходе поступления вызовов в процессе соединения в СИСТЕМЕ ATM. Механизм соответствует системе организации очереди с постоянным временем обслуживания (длина ячейки =53 байта) и ограниченным буфером. Если процесс поступления вызовов - Пуассоновский процесс, то мы имеем 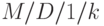 -систему. Размер утечки из "ведра" соответствует средней интенсивности поступления заявок, принимаемых за достаточно длительный период, тогда как размер "ведра" (буфер) обозначает избыток, разрешенный в течение короткого временного интервала. В системе ATM механизм работает как виртуальная система организации очереди, где ячейка либо принимается немедленно, либо отклоняется. Счетчик указывает значение функции нагрузки. Контракт между оператором (сеть) и пользователем (соединение) согласовывает размер утечки и "ведра" и основан на информации о том, какое качество обслуживания способна гарантировать сеть.
-систему. Размер утечки из "ведра" соответствует средней интенсивности поступления заявок, принимаемых за достаточно длительный период, тогда как размер "ведра" (буфер) обозначает избыток, разрешенный в течение короткого временного интервала. В системе ATM механизм работает как виртуальная система организации очереди, где ячейка либо принимается немедленно, либо отклоняется. Счетчик указывает значение функции нагрузки. Контракт между оператором (сеть) и пользователем (соединение) согласовывает размер утечки и "ведра" и основан на информации о том, какое качество обслуживания способна гарантировать сеть.
Упражнение
Сначала рассмотрим систему организации очереди 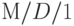 , в которой примем Пуассоновский поток вызовов с интенсивностью
, в которой примем Пуассоновский поток вызовов с интенсивностью 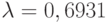 вызова в единицу времени, постоянное время обслуживания, которое мы выбираем как единицу времени, и один сервер. Число мест ожидания неограниченно, и система находится в статистическом равновесии.
вызова в единицу времени, постоянное время обслуживания, которое мы выбираем как единицу времени, и один сервер. Число мест ожидания неограниченно, и система находится в статистическом равновесии.
- Найти первые вероятности состояния
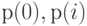 и
и 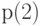 (заметьте, что
(заметьте, что 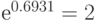 ). Мы принимаем, что есть только одно место ожидания
). Мы принимаем, что есть только одно место ожидания 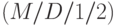
- Найти от вероятности состояний в вопросе 1, применяя формулу Кейлсона (Keilson) в секции 13.3.4, вероятности состояния
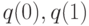 или
или 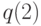 в конечной системе.
в конечной системе. -
Какова вероятность, что вызов будет:
- обслужен немедленно?
- задержан перед обслуживанием?
- отклонен?
- Найти, используя теорему Литла, среднее время ожидания для ожидающих в очереди клиентов (при положительном значении время ожидания).
- Какова вероятность, что период занятости (период, когда сервер занят) имеет продолжительность одну единицу времени?
- Найти вероятность, что период занятости имеет продолжительность
 единиц времени.
единиц времени.
Упражнение 13.21. Приоритетная система организации очереди
Мы рассматриваем систему организации очереди с одним обслуживающим прибором  , куда заявки от клиентов прибывают согласно Пуассоновскому процессу. Есть три типа клиентов.
, куда заявки от клиентов прибывают согласно Пуассоновскому процессу. Есть три типа клиентов.
- Тип 1. Интенсивность поступления
 вызова в единицу времени. Время обслуживания: константа со средней величиной 1 единица времени.
вызова в единицу времени. Время обслуживания: константа со средней величиной 1 единица времени. - Тип 2. Интенсивность поступления
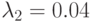 вызова в единицу времени. Время обслуживания: экспоненциально распределенное со средней величиной 10 единиц времени.
вызова в единицу времени. Время обслуживания: экспоненциально распределенное со средней величиной 10 единиц времени. - Тип 3. Интенсивность поступления
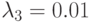 вызова в единицу времени. Время обслуживания: плоское распределение со средней величиной 40 единиц времени и коэффициентом
вызова в единицу времени. Время обслуживания: плоское распределение со средней величиной 40 единиц времени и коэффициентом  формы =10.
формы =10.
- Найти предложенную нагрузку для каждого типа и полной предложенной нагрузки.
-
Найти среднее время ожидания для случайного клиента, когда нет никакого приоритета.
Тип 1 и тип 2 имеют приоритет возвращения к работе по отношению к типу 3, так, что на эти два типа не влияет тип 3.
Тип 1 не имеет приоритета по сравнению с двумя типами.
- Найти среднее время ожидания для типа 1 и 2.
- Найти среднее время ожидания для типа 3 (тип 1 и тип 2 могут быть объединены в один тип по отношению к типу 3).
- Найти среднее время ожидания для всех запросов для каждого типа клиентов, когда только этот тип предлагается системе.
Упражнение 13.22. Система организации приоритетной очереди аэропорта
Рассмотрим аэропорт, где сервер обслуживает единственную взлетно-посадочную полосу. Нагрузка в течение одного утреннего часа пик состоит из прибывающих и взлетающих самолетов. Оба вида использования взлетно-посадочной полосы осуществляются следующим образом.
-
Приземление: 10 самолетов прибывают в час. Среднее время обслуживания
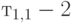 [минуты] и второй момент времени обслуживания
[минуты] и второй момент времени обслуживания 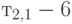 [минуты2].
[минуты2]. -
Старт: 20 самолетов отбывают в час. Среднее время обслуживания
 [минуты] и второй момент времени обслуживания
[минуты] и второй момент времени обслуживания 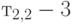 [минуты2].
[минуты2].
- Найти предложенную нагрузку для каждого типа и полную предложенную нагрузку.
- Найти полную интенсивность поступления и среднее время обслуживания для всех самолетов и использовать это для проверки полной предложенной нагрузки.
- Найти среднее время ожидания для произвольного самолета, когда у него нет никакого приоритета.
- Найти среднее время ожидания для обоих типов, когда приземление самолета имеет приоритет перед взлетающими самолетами. Покажите, что для этой системы выполняется закон сохранения.
Упражнение 13.23. Система с мультисервисной приоритетной очередью
Мы рассматриваем С-Эрланговскую систему времени Эрл (Пуассоновский поток вызовов и экспоненциальное время обслуживания). Среднее время обслуживания - 60 секунд.
- Найти интенсивность поступления вызовов.
- Найти вероятность задержки, используя для вычисления рекурсивную В-формулу Эрланга и отношения между формулами В и С. (Детали вычисления должны быть представлены в ответе, и результат -
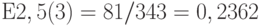 ).
). -
Найти среднее время ожидания для всех клиентов.
Мы теперь делим вышеупомянутую предложенную нагрузку на ДЕ приоритетных класса.
- Класс 1: А = 1 Эрл. для высокоприоритетных клиентов.
- Класс 2: А = 2 Эрл. для низкоприоритетных клиентов.
Оба класса все еще имеют одинаковое среднее время обслуживани 60 секунд.
Сначала рассмотрим неприоритетную стратегию возвращения к работе
- Найти среднее время ожидания для каждого из двух классов.
-
Показать, что закон сохранения верен для этой системы.
Рассмотрим приоритетную стратегию возвращения к работе. Из-; свойств экспоненциального распределения - закон сохранения таю* справедлив для этой модели.
- Найти среднее время ожидания для каждого из двух классов, (дано:
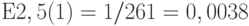 ).
).