Алгоритмы хеширования данных
Цель лекции: изучить построение функции хеширования и алгоритмов хеширования данных и научиться разрабатывать алгоритмы открытого и закрытого хеширования при решении задач на языке C++.
Процесс поиска данных в больших объемах информации сопряжен с временными затратами, которые обусловлены необходимостью просмотра и сравнения с ключом поиска значительного числа элементов. Сокращение поиска возможно осуществить путем локализации области просмотра. Например, отсортировать данные по ключу поиска, разбить на непересекающиеся блоки по некоторому групповому признаку или поставить в соответствие реальным данным некий код, который упростит процедуру поиска.
В настоящее время используется широко распространенный метод обеспечения быстрого доступа к информации, хранящейся во внешней памяти – хеширование.
Хеширование (или хэширование, англ. hashing ) – это преобразование входного массива данных определенного типа и произвольной длины в выходную битовую строку фиксированной длины. Такие преобразования также называются хеш-функциями или функциями свертки, а их результаты называют хешем, хеш-кодом, хеш-таблицей или дайджестом сообщения (англ. message digest ).
Хеш-таблица – это структура данных, реализующая интерфейс ассоциативного массива, то есть она позволяет хранить пары вида "ключ- значение" и выполнять три операции: операцию добавления новой пары, операцию поиска и операцию удаления пары по ключу. Хеш-таблица является массивом, формируемым в определенном порядке хеш-функцией.
Принято считать, что хорошей, с точки зрения практического применения, является такая хеш-функция, которая удовлетворяет следующим условиям:
- функция должна быть простой с вычислительной точки зрения;
- функция должна распределять ключи в хеш-таблице наиболее равномерно;
- функция не должна отображать какую-либо связь между значениями ключей в связь между значениями адресов;
- функция должна минимизировать число коллизий – то есть ситуаций, когда разным ключам соответствует одно значение хеш-функции (ключи в этом случае называются синонимами ).
При этом первое свойство хорошей хеш-функции зависит от характеристик компьютера, а второе – от значений данных.
Если бы все данные были случайными, то хеш-функции были бы очень простые (например, несколько битов ключа). Однако на практике случайные данные встречаются достаточно редко, и приходится создавать функцию, которая зависела бы от всего ключа. Если хеш-функция распределяет совокупность возможных ключей равномерно по множеству индексов, то хеширование эффективно разбивает множество ключей. Наихудший случай – когда все ключи хешируются в один индекс.
При возникновении коллизий необходимо найти новое место для хранения ключей, претендующих на одну и ту же ячейку хеш-таблицы. Причем, если коллизии допускаются, то их количество необходимо минимизировать. В некоторых специальных случаях удается избежать коллизий вообще. Например, если все ключи элементов известны заранее (или очень редко меняются), то для них можно найти некоторую инъективную хеш-функцию, которая распределит их по ячейкам хеш-таблицы без коллизий. Хеш-таблицы, использующие подобные хеш-функции, не нуждаются в механизме разрешения коллизий, и называются хеш-таблицами с прямой адресацией.
Хеш-таблицы должны соответствовать следующим свойствам.
- Выполнение операции в хеш-таблице начинается с вычисления хеш-функции от ключа. Получающееся хеш-значение является индексом в исходном массиве.
- Количество хранимых элементов массива, деленное на число возможных значений хеш-функции, называется коэффициентом заполнения хеш-таблицы ( load factor ) и является важным параметром, от которого зависит среднее время выполнения операций.
- Операции поиска, вставки и удаления должны выполняться в среднем за время O(1). Однако при такой оценке не учитываются возможные аппаратные затраты на перестройку индекса хеш-таблицы, связанную с увеличением значения размера массива и добавлением в хеш-таблицу новой пары.
- Механизм разрешения коллизий является важной составляющей любой хеш-таблицы.
Хеширование полезно, когда широкий диапазон возможных значений должен быть сохранен в малом объеме памяти, и нужен способ быстрого, практически произвольного доступа. Хэш-таблицы часто применяются в базах данных, и, особенно, в языковых процессорах типа компиляторов и ассемблеров, где они повышают скорость обработки таблицы идентификаторов. В качестве использования хеширования в повседневной жизни можно привести примеры распределение книг в библиотеке по тематическим каталогам, упорядочивание в словарях по первым буквам слов, шифрование специальностей в вузах и т.д.
Методы разрешения коллизий
Коллизии осложняют использование хеш-таблиц, так как нарушают однозначность соответствия между хеш-кодами и данными. Тем не менее, существуют способы преодоления возникающих сложностей:
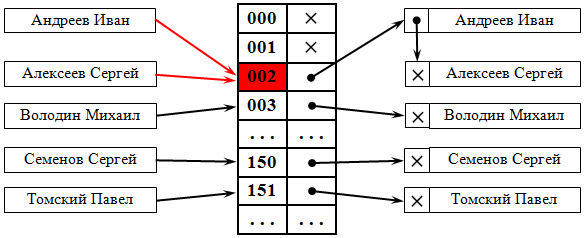
Метод цепочек. Технология сцепления элементов состоит в том, что элементы множества, которым соответствует одно и то же хеш-значение, связываются в цепочку-список. В позиции номер i хранится указатель на голову списка тех элементов, у которых хеш-значение ключа равно i ; если таких элементов в множестве нет, в позиции i записан NULL. На рис. 38.1 демонстрируется реализация метода цепочек при разрешении коллизий. На ключ 002 претендуют два значения, которые организуются в линейный список.
Каждая ячейка массива является указателем на связный список (цепочку) пар ключ-значение, соответствующих одному и тому же хеш-значению ключа. Коллизии просто приводят к тому, что появляются цепочки длиной более одного элемента.
Операции поиска или удаления данных требуют просмотра всех элементов соответствующей ему цепочки, чтобы найти в ней элемент с заданным ключом. Для добавления данных нужно добавить элемент в конец или начало соответствующего списка, и, в случае если коэффициент заполнения станет слишком велик, увеличить размер массива и перестроить таблицу.
При предположении, что каждый элемент может попасть в любую позицию таблицы с равной вероятностью и независимо от того, куда попал любой другой элемент, среднее время работы операции поиска элемента составляет O(1+k), где k – коэффициент заполнения таблицы.
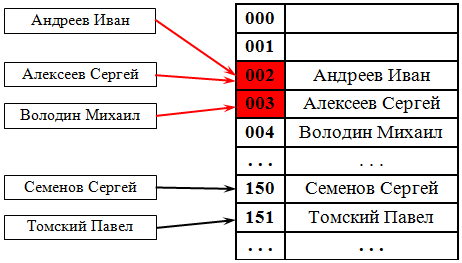
Метод открытой адресации. В отличие от хеширования с цепочками, при открытой адресации никаких списков нет, а все записи хранятся в самой хеш-таблице. Каждая ячейка таблицы содержит либо элемент динамического множества, либо NULL.
В этом случае, если ячейка с вычисленным индексом занята, то можно просто просматривать следующие записи таблицы по порядку до тех пор, пока не будет найден ключ K или пустая позиция в таблице. Для вычисления шага можно также применить формулу, которая и определит способ изменения шага. На рис. 38.2 разрешение коллизий осуществляется методом открытой адресации. Два значения претендуют на ключ 002, для одного из них находится первое свободное (еще незанятое) место в таблице.
При любом методе разрешения коллизий необходимо ограничить длину поиска элемента. Если для поиска элемента необходимо более 3 – 4 сравнений, то эффективность использования такой хеш-таблицы пропадает и ее следует реструктуризировать (т.е. найти другую хеш-функцию), чтобы минимизировать количество сравнений для поиска элемента
Для успешной работы алгоритмов поиска, последовательность проб должна быть такой, чтобы все ячейки хеш-таблицы оказались просмотренными ровно по одному разу.
Удаление элементов в такой схеме несколько затруднено. Обычно поступают так: заводят логический флаг для каждой ячейки, помечающий, удален ли элемент в ней или нет. Тогда удаление элемента состоит в установке этого флага для соответствующей ячейки хеш-таблицы, но при этом необходимо модифицировать процедуру поиска существующего элемента так, чтобы она считала удаленные ячейки занятыми, а процедуру добавления – чтобы она их считала свободными и сбрасывала значение флага при добавлении.