Рекурсия и рекурсивные алгоритмы

Цель лекции: изучить понятие, виды рекурсии и рекурсивную триаду, научиться разрабатывать рекурсивную триаду при решении задач на языке C++.

Одной из идей процедурного программирования, которая оформилась в начале шестидесятых годов ХХ века, стало активное применение в практике программирования некоторого метода, основанного на организации серий взаимных обращений программ (функций) друг к другу. Вопросы об эффективности использования данного метода при разработке алгоритмических моделей актуальны и в настоящее время, несмотря на существование различных парадигм программирования, создание новых и совершенствование существующих языков программирования. Речь идет о рекурсивном методе в программировании, который рассматривается альтернативным по отношению к итерационному.

Рекурсия – это определение объекта через обращение к самому себе.

Рекурсивный алгоритм – это алгоритм, в описании которого прямо или косвенно содержится обращение к самому себе. В технике процедурного программирования данное понятие распространяется на функцию, которая реализует решение отдельного блока задачи посредством вызова из своего тела других функций, в том числе и себя самой. Если при этом на очередном этапе работы функция организует обращение к самой себе, то такая функция является рекурсивной.

Прямое обращение функции к самой себе предполагает, что в теле функции содержится вызов этой же функции, но с другим набором фактических параметров. Такой способ организации работы называется прямой рекурсией. Например, чтобы найти сумму первых n натуральных чисел, надо сумму первых (n-1) чисел сложить с числом n, то есть имеет место зависимость: S_n=S_n-1+n. Вычисление происходит с помощью аналогичных рассуждений. Такая цепочка взаимных обращений в конечном итоге сведется к вычислению суммы одного первого элемента, которая равна самому элементу.

При косвенном обращении функция содержит вызовы других функций из своего тела. При этом одна или несколько из вызываемых функций на определенном этапе обращаются к исходной функции с измененным набором входных параметров. Такая организация обращений называется косвенной рекурсией. Например, поиск максимального элемента в массиве размера n можно осуществлять как поиск максимума из двух чисел: одно их них – это последний элемент массива, а другое является максимальным элементом в массиве размера (n-1). Для нахождения максимального элемента массива размера (n-1) применяются аналогичные рассуждения. В итоге решение сводится к поиску максимального из первых двух элементов массива.

Рекурсивный метод в программировании предполагает разработку решения задачи, основываясь на свойствах рекурсивности отдельных объектов или закономерностей. При этом исходная задача сводится к решению аналогичных подзадач, которые являются более простыми и отличаются другим набором параметров.

Разработке рекурсивных алгоритмов предшествует рекурсивная триада – этапы моделирования задачи, на которых определяется набор параметров и соотношений между ними. Рекурсивную триаду составляют параметризация, выделение базы и декомпозиция.

На этапе параметризации из постановки задачи выделяются параметры, которые описывают исходные данные. При этом некоторые дальнейшие разработки решения могут требовать введения дополнительных параметров, которые не оговорены в условии, но используются при составлении зависимостей. Необходимость в дополнительных параметрах часто возникает также при решении задач оптимизации рекурсивных алгоритмов, в ходе которых сокращается их временная сложность.

Выделение базы рекурсии предполагает нахождение в решаемой задаче тривиальных случаев, результат для которых очевиден и не требует проведения расчетов. Верно найденная база рекурсии обеспечивает завершенность рекурсивных обращений, которые в конечном итоге сводятся к базовому случаю. Переопределение базы или ее динамическое расширение в ходе решения задачи часто позволяют оптимизировать рекурсивный алгоритм за счет достижения базового случая за более короткий путь обращений.

Декомпозиция представляет собой сведение общего случая к более простым подзадачам, которые отличаются от исходной задачи набором входных данных. Декомпозиционные зависимости описывают не только связь между задачей и подзадачами, но и характер изменения значений параметров на очередном шаге. От выбранных отношений зависит трудоемкость алгоритма, так как для одной и той же задачи могут быть составлены различные зависимости. Пересмотр отношений декомпозиции целесообразно проводить комплексно, то есть параллельно с корректировкой параметров и анализом базовых случаев.

Анализ трудоемкости рекурсивных алгоритмов методом подсчета вершин дерева рекурсии

Рекурсивные алгоритмы относятся к классу алгоритмов с высокой ресурсоемкостью, так как при большом количестве самовызовов рекурсивных функций происходит быстрое заполнение стековой области. Кроме того, организация хранения и закрытия очередного слоя рекурсивного стека являются дополнительными операциями, требующими временных затрат. На трудоемкость рекурсивных алгоритмов влияет и количество передаваемых функцией параметров.

Рассмотрим один из методов анализа трудоемкости рекурсивного алгоритма, который строится на основе подсчета вершин рекурсивного дерева. Для оценки трудоемкости рекурсивных алгоритмов строится полное дерево рекурсии. Оно представляет собой граф, вершинами которого являются наборы фактических параметров при всех вызовах функции, начиная с первого обращения к ней, а ребрами – пары таких наборов, соответствующих взаимным вызовам. При этом вершины дерева рекурсии соответствуют фактическим вызовам рекурсивных функций. Следует заметить, что одни и те же наборы параметров могут соответствовать разным вершинам дерева. Корень полного дерева рекурсивных вызовов – это вершина полного дерева рекурсии, соответствующая начальному обращению к функции.

Важной характеристикой рекурсивного алгоритма является глубина рекурсивных вызовов – наибольшее одновременное количество рекурсивных обращений функции, определяющее максимальное количество слоев рекурсивного стека, в котором осуществляется хранение отложенных вычислений. Количество элементов полных рекурсивных обращений всегда не меньше глубины рекурсивных вызовов. При разработке рекурсивных программ необходимо учитывать, что глубина рекурсивных вызовов не должна превосходить максимального размера стека используемой вычислительной среды.

При этом объем рекурсии - это одна из характеристик сложности рекурсивных вычислений для конкретного набора параметров, представляющая собой количество вершин полного рекурсивного дерева без единицы.

Будем использовать следующие обозначения для конкретного входного параметра D:

R(D) – общее число вершин дерева рекурсии,

R_V(D) – объем рекурсии без листьев (внутренние вершины),

R_L(D) – количество листьев дерева рекурсии,

H_R(D) – глубина рекурсии.

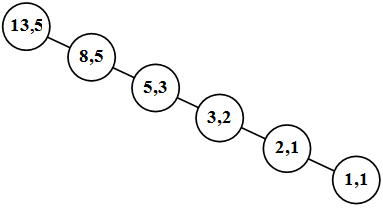
Например, для вычисления n -го члена последовательности Фибоначчи разработана следующая рекурсивная функция:

int Fib(int n){ //n – номер члена последовательности
  if(n<3) return 1; //база рекурсии
  return Fib(n-1)+Fib(n-2); //декомпозиция 
}

Тогда полное дерево рекурсии для вычисления пятого члена последовательности Фибоначчи будет иметь вид ( рис. 34.1):

Рис. 34.1. Полное дерево рекурсии для пятого члена последовательности Фибоначчи

Характеристиками рассматриваемого метода оценки алгоритма будут следующие величины.

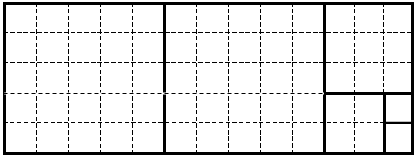
Пример 1. Задача о разрезании прямоугольника на квадраты.

Дан прямоугольник, стороны которого выражены натуральными числами. Разрежьте его на минимальное число квадратов с натуральными сторонами. Найдите число получившихся квадратов.

Разработаем рекурсивную триаду.

Параметризация: m, n – натуральные числа, соответствующие размерам прямоугольника.

База рекурсии: для m=n число получившихся квадратов равно 1, так как данный прямоугольник уже является квадратом.

Декомпозиция: если 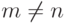, то возможны два случая m < n или m > n. Отрежем от прямоугольника наибольший по площади квадрат с натуральными сторонами. Длина стороны такого квадрата равна наименьшей из сторон прямоугольника. После того, как квадрат будет отрезан, размеры прямоугольника станут следующие: большая сторона уменьшится на длину стороны квадрата, а меньшая не изменится. Число искомых квадратов будет вычисляться как число квадратов, на которые будет разрезан полученный прямоугольник, плюс один (отрезанный квадрат). К получившемуся прямоугольнику применим аналогичные рассуждения: проверим на соответствие базе или перейдем к декомпозиции ( рис. 34.2).

Рис. 34.2. Пример разрезания прямоугольника 13x5 на квадраты

#include "stdafx.h"
#include <iostream>
using namespace std;
int kv(int m,int n);

int _tmain(int argc, _TCHAR* argv[]) {
  int a,b,k;
  printf("Введите стороны прямоугольника->");
  scanf("%d%d",&a,&b);
  k = kv(a,b);
  printf("Прямоугольник со сторонами %d и %d можно разрезать 
          на %d квадратов",a,b,k);
  system("pause");
  return 0;
}

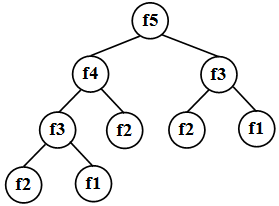
int kv(int m,int n){ //m,n – стороны прямоугольника
  if(m==n) return 1; //база рекурсии
  if(m>n) return 1+kv(m-n,n); //декомпозиция для m>n
  return 1+kv(m,n-m); //декомпозиция для m<n
}

Характеристиками рассматриваемого метода оценки алгоритма будут следующие величины ( рис. 34.3).

D = (13, 5)	D = (m, n), m n, худший случай
R(D)=6	R(D)=m
RV(D)=4	RV(D)=m-2
RL(D)=1	RL(D)=1
HR(D)=6	HR(D)=m

Рис. 34.3. Пример полного дерева рекурсии для разрезания прямоугольника 13x5 на квадраты