Алгоритмы поиска на основе деревьев
Цель лекции: изучить алгоритмы поиска на основе деревьев, научиться решать задачи поиска через построение упорядоченного, случайного, оптимального или сбалансированного в высоту деревьев на языке C++.
Поиск данных, являясь одним из приоритетных направлений работы с данными, предполагает использование соответствующих алгоритмов в зависимости от ряда факторов: способ представления данных, упорядоченность множества поиска, объем данных, расположение их во внешней или во внутренней памяти. Поиск – процесс нахождения конкретной информации в ранее созданном множестве данных. Как правило, данные представляют собой структуры, каждая из которых имеет хотя бы один ключ – значение определенного поля конкретной структуры. Ключ поиска – это поле, по значению которого происходит поиск.
Рассмотрим организацию поиска данных, имеющих древовидную структуру. Анализируя дерево только с точки зрения представления данных в виде иерархической структуры, заметим, что выигрыша при организации поиска не получится. Сравнение ключа поиска с эталоном необходимо провести для всех элементов дерева.
Уменьшить число сравнений ключей с эталоном возможно, если выполнить организацию дерева особым образом, то есть расположить его элементы по определенным правилам. При этом в процессе поиска будет просмотрено не все дерево, а отдельное поддерево. Такой подход позволяет классифицировать деревья в зависимости от правил построения. Выделим некоторые популярные виды деревьев, на основе которых рассмотрим организацию поиска.
Двоичные (бинарные) деревья
Двоичные деревья представляют собой иерархическую структуру, в которой каждый узел имеет не более двух потомков. То есть двоичное дерево либо является пустым, либо состоит из данных и двух поддеревьев (каждое из которых может быть пустым). При этом каждое поддерево в свою очередь тоже является деревом. Поиск на таких структурах не дает выигрыша по выполнению по сравнению с линейными структурами того же размера, так как необходимо в худшем случае выполнить обход всего дерева. Поэтому интерес представляют двоичные упорядоченные деревья.
Двоичные упорядоченные деревья
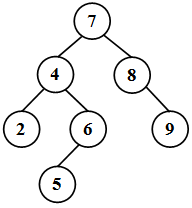
Двоичное дерево упорядоченно, если для любой его вершины x справедливы такие свойства ( рис. 40.1):
- все элементы в левом поддереве меньше элемента, хранимого в x,
- все элементы в правом поддереве больше элемента, хранимого в x,
- все элементы дерева различны.
Если в дереве выполняются первые два свойства, но встречаются одинаковые элементы, то такое дерево является частично упорядоченным. В дальнейшем будет идти речь только о двоичных упорядоченных деревьях. Основными операциями, производимыми с упорядоченным деревом, являются:
Пример 1. Программная реализация основных операций бинарного дерева поиска.
#include "stdafx.h"
#include <iostream>
#include <time.h>
using namespace std;
typedef int T; // тип элемента
#define compLT(a,b) (a < b)
#define compEQ(a,b) (a == b)
typedef struct Node_ {
T data; // значение узла
struct Node_ *left;// левый потомок
struct Node_ *right;// правый потомок
struct Node_ *parent;// родитель
} Node;
Node *root = NULL; //корень бинарного дерева поиска
Node* insertNode(T data);
void deleteNode(Node *z);
Node* findNode(T data);
void printTree(Node *node, int l = 0);
int _tmain(int argc, _TCHAR* argv[]){
int i, *a, maxnum;
cout << "Введите количество элементов maxnum : ";
cin >> maxnum;
cout << endl;
a = new int[maxnum];
srand(time(NULL)*1000);
// генерация массива
for (i = 0; i < maxnum; i++)
a[i] = rand();
cout << "Вывод сгенерированной последовательности" << endl;
for (i = 0; i < maxnum; i++)
cout << a[i] << " ";
cout << endl;
cout << endl;
// добавление элементов в бинарное дерево поиска
for (i = 0; i < maxnum; i++) {
insertNode(a[i]);
}
cout << "Вывод бинарного дерева поиска" << endl;
printTree(root);
cout << endl;
// поиск элементов по бинарному дереву поиска
for (i = maxnum-1; i >= 0; i--) {
findNode(a[i]);
}
// очистка бинарного дерева поиска
for (i = 0; i < maxnum; i++) {
deleteNode(findNode(a[i]));
}
system("pause");
return 0;
}
//функция выделения памяти для нового узла и вставка в дерево
Node* insertNode(T data) {
Node *x, *current, *parent;
current = root;
parent = 0;
while (current) {
if ( data == current->data ) return (current);
parent = current;
current = data < current->data ?
current->left : current->right;
}
x = new Node;
x->data = data;
x->parent = parent;
x->left = NULL;
x->right = NULL;
if(parent)
if( x->data < parent->data )
parent->left = x;
else
parent->right = x;
else
root = x;
return(x);
}
//функция удаления узла из дерева
void deleteNode(Node *z) {
Node *x, *y;
if (!z || z == NULL) return;
if (z->left == NULL || z->right == NULL)
y = z;
else {
y = z->right;
while (y->left != NULL) y = y->left;
}
if (y->left != NULL)
x = y->left;
else
x = y->right;
if (x) x->parent = y->parent;
if (y->parent)
if (y == y->parent->left)
y->parent->left = x;
else
y->parent->right = x;
else
root = x;
if (y != z) {
y->left = z->left;
if (y->left) y->left->parent = y;
y->right = z->right;
if (y->right) y->right->parent = y;
y->parent = z->parent;
if (z->parent)
if (z == z->parent->left)
z->parent->left = y;
else
z->parent->right = y;
else
root = y;
free (z);
}
else {
free (y);
}
}
//функция поиска узла, содержащего data
Node* findNode(T data) {
Node *current = root;
while(current != NULL)
if(compEQ(data, current->data))
return (current);
else
current = compLT(data, current->data) ?
current->left : current->right;
return(0);
}
//функция вывода бинарного дерева поиска
void printTree(Node *node, int l){
int i;
if (node != NULL) {
printTree(node->right, l+1);
for (i=0; i < l; i++) cout << " ";
printf ("%4ld", node->data);
printTree(node->left, l+1);
}
else cout << endl;
}
Листинг
.
Алгоритм удаления элемента более трудоемкий, так как надо соблюдать упорядоченность дерева. При удалении может случиться, что удаляемый элемент находится не в листе, то есть вершина имеет ссылки на реально существующие поддеревья. Эти поддеревья терять нельзя, а присоединить два поддерева на одно освободившееся после удаления место невозможно. Поэтому необходимо поместить на освободившееся место либо самый правый элемент из левого поддерева, либо самый левый из правого поддерева. Упорядоченность дерева при этом не нарушится. Удобно придерживаться одной стратегии, например, заменять самый левый элемент из правого поддерева. Нельзя забывать, что при замене вершина, на которую производится замена, может иметь правое поддерево. Это поддерево необходимо поставить вместо перемещаемой вершины.
Временная сложность этих алгоритмов (она одинакова для этих алгоритмов, так как в их основе лежит поиск) оценим для наилучшего и наихудшего случая. В лучшем случае, то есть случае полного двоичного дерева, получаем сложность Omin(log n). В худшем случае дерево может выродиться в список. Такое может произойти, например, при добавлении элементов в порядке возрастания. При работе со списком в среднем придется просмотреть половину списка. Это даст сложность Omax(n).
Случайные деревья
Случайные деревья поиска представляют собой упорядоченные бинарные деревья поиска, при создании которых элементы (их ключи) вставляются в случайном порядке.
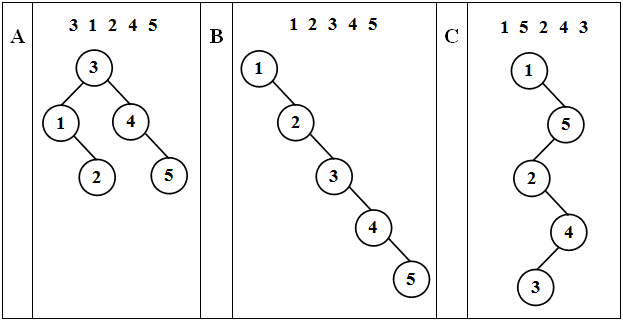
При создании таких деревьев используется тот же алгоритм, что и при добавлении вершины в бинарное дерево поиска. Будет ли созданное дерево случайным или нет, зависит от того, в каком порядке поступают элементы для добавления. Примеры различных деревьев, создаваемых при различном порядке поступления элементов, приведены ниже ( рис. 40.2).
При поступлении элементов в случайном порядке получаем дерево с минимальной высотой h (рис. 40.2А), при этом минимизируется время поиска элемента в дереве, которое пропорционально O(log n). При поступлении элементов в упорядоченном виде (рис. 40.2В) или в порядке с единичными сериями монотонности (рис. 40.2С) происходит построение вырожденных деревьев поиска (оно вырождено в линейный список), что нисколько не сокращает время поиска, которое составляет O(n).