Алгоритмы на графах. Алгоритмы нахождения кратчайшего пути
Цель лекции: изучить основные алгоритмы поиска кратчайшего пути и научиться решать задачи поиска кратчайшего пути на основе алгоритмов Дейкстры, Флойда и переборных алгоритмов.
Нахождение кратчайшего пути на сегодняшний день является жизненно необходимой задачей и используется практически везде, начиная от нахождения оптимального маршрута между двумя объектами на местности (например, кратчайший путь от дома до университета), в системах автопилота, для нахождения оптимального маршрута при перевозках, коммутации информационного пакета в сетях и т.п.
Кратчайший путь рассматривается при помощи некоторого математического объекта, называемого графом. Поиск кратчайшего пути ведется между двумя заданными вершинами в графе. Результатом является путь, то есть последовательность вершин и ребер, инцидентных двум соседним вершинам, и его длина.
Рассмотрим три наиболее эффективных алгоритма нахождения кратчайшего пути:
Указанные алгоритмы легко выполняются при малом количестве вершин в графе. При увеличении их количества задача поиска кратчайшего пути усложняется.
Алгоритм Дейкстры
Данный алгоритм является алгоритмом на графах, который изобретен нидерландским ученым Э. Дейкстрой в 1959 году. Алгоритм находит кратчайшее расстояние от одной из вершин графа до всех остальных и работает только для графов без ребер отрицательного веса.
Каждой вершине приписывается вес – это вес пути от начальной вершины до данной. Также каждая вершина может быть выделена. Если вершина выделена, то путь от нее до начальной вершины кратчайший, если нет – то временный. Обходя граф, алгоритм считает для каждой вершины маршрут, и, если он оказывается кратчайшим, выделяет вершину. Весом данной вершины становится вес пути. Для всех соседей данной вершины алгоритм также рассчитывает вес, при этом ни при каких условиях не выделяя их. Алгоритм заканчивает свою работу, дойдя до конечной вершины, и весом кратчайшего пути становится вес конечной вершины.
Алгоритм Дейкстры
Шаг 1. Всем вершинам, за исключением первой, присваивается вес равный бесконечности, а первой вершине – 0.
Шаг 2. Все вершины не выделены.
Шаг 3. Первая вершина объявляется текущей.
Шаг 4. Вес всех невыделенных вершин пересчитывается по формуле: вес невыделенной вершины есть минимальное число из старого веса данной вершины, суммы веса текущей вершины и веса ребра, соединяющего текущую вершину с невыделенной.
Шаг 5. Среди невыделенных вершин ищется вершина с минимальным весом. Если таковая не найдена, то есть вес всех вершин равен бесконечности, то маршрут не существует. Следовательно, выход. Иначе, текущей становится найденная вершина. Она же выделяется.
Шаг 6. Если текущей вершиной оказывается конечная, то путь найден, и его вес есть вес конечной вершины.
Шаг 7. Переход на шаг 4.
В программной реализации алгоритма Дейкстры построим множество S вершин, для которых кратчайшие пути от начальной вершины уже известны. На каждом шаге к множеству S добавляется та из оставшихся вершин, расстояние до которой от начальной вершины меньше, чем для других оставшихся вершин. При этом будем использовать массив D, в который записываются длины кратчайших путей для каждой вершины. Когда множество S будет содержать все вершины графа, тогда массив D будет содержать длины кратчайших путей от начальной вершины к каждой вершине.
Помимо указанных массивов будем использовать матрицу длин C, где элемент C[i,j] –длина ребра (i,j), если ребра нет, то ее длина полагается равной бесконечности, то есть больше любой фактической длины ребер. Фактически матрица C представляет собой матрицу смежности, в которой все нулевые элементы заменены на бесконечность.
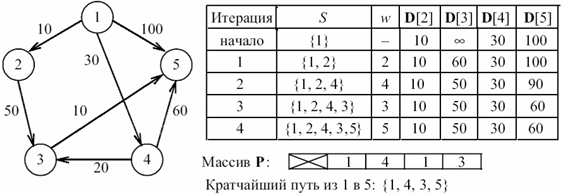
Для определения самого кратчайшего пути введем массив P вершин, где P[v] будет содержать вершину, непосредственно предшествующую вершине v в кратчайшем пути ( рис. 45.1).
//Описание функции алгоритма Дейкстры
void Dijkstra(int n, int **Graph, int Node){
bool *S = new bool[n];
int *D = new int[n];
int *P = new int[n];
int i, j;
int Max_Sum = 0;
for (i = 0 ; i < n ; i++)
for (j = 0 ; j < n ; j++)
Max_Sum += Graph[i][j];
for (i = 0 ; i < n ; i++)
for (j = 0 ; j < n ; j++)
if (Graph[i][j] == 0)
Graph[i][j] = Max_Sum;
for (i = 0 ; i < n ; i++){
S[i] = false;
P[i] = Node;
D[i] = Graph[Node][i];
}
S[Node] = true;
P[Node] = -1;
for ( i = 0 ; i < n - 1 ; i++ ){
int w = 0;
for ( j = 1 ; j < n ; j++ ){
if (!S[w]){
if (!S[j] && D[j] <= D[w])
w = j;
}
else w++;
}
S[w] = true;
for ( j = 1 ; j < n ; j++ )
if (!S[j])
if (D[w] + Graph[w][j] < D[j]){
D[j] = D[w] + Graph[w][j];
P[j] = w;
}
}
for ( i = 0 ; i < n ; i++ )
printf("%5d",D[i]);
cout << endl;
for ( i = 0 ; i < n ; i++ )
printf("%5d",P[i]+1);
cout << endl;
delete [] P;
delete [] D;
delete [] S;
}Сложность алгоритма Дейкстры зависит от способа нахождения вершины, а также способа хранения множества непосещенных вершин и способа обновления длин.
Если для представления графа использовать матрицу смежности, то время выполнения этого алгоритма имеет порядок O(n2), где n – количество вершин графа.