Рекурсия и рекурсивные алгоритмы
Лабораторная работа 34. Рекурсия и рекурсивные алгоритмы
Цель работы: изучить понятие, виды рекурсии и рекурсивную триаду, научиться разрабатывать рекурсивную триаду при решении задач на языке C++.
При выполнении лабораторной работы для каждого задания требуется написать программу на языке С++, которая получает на входе числовые данные, выполняет их обработку в соответствии с требованиями задания и выводит результат на экран. Для обработки данных необходимо реализовать рекурсивную функцию. Ввод данных осуществляется с клавиатуры с учетом требований к входным данным, содержащихся в постановке задачи (ввод данных сопровождайте диалогом). Ограничениями на входные данные является допустимый диапазон значений используемых числовых типов в языке С++.
Теоретические сведения.
Ознакомьтесь с материалом лекции 34.
Задания к лабораторной работе.
Выполните приведенные ниже задания.
- Разработайте рекурсивную функцию, подсчитывающую количество способов разбиения выпуклого многоугольника на треугольники непересекающимися диагоналями.
- В Фибоначчиевой системе счисления числа формируются по правилам.
- Используются только символы 0 и 1;
- Каждый разряд соответствует элементу последовательности Фибоначчи 1, 2, 3, 5, 8, …, то есть указывает на наличие или отсутствие такового;
- В соседних разрядах не могут стоять символы 1, так как это автоматически означает формирование следующего за ними разряда. Например, 1710 = 1310 + 310 + 110 = 100101ф.
- Найдите походящие дроби рационального числа x/y ( x – неотрицательно, y – положительно). Например,
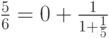 , то есть для х = 5, y = 6 ответом будет последовательность [0; 1, 5].
, то есть для х = 5, y = 6 ответом будет последовательность [0; 1, 5]. - Вычислите определитель квадратной матрицы размера nxn.
Указания к выполнению работы.
Каждое задание необходимо решить в соответствии с изученными рекурсивными методами решения задач и методами обработки числовых данных в языке С++. Перед реализацией кода каждой задачи необходимо разработать рекурсивную триаду в соответствии с постановкой задачи: выполнить параметризацию, выделить базу и оформить декомпозицию рекурсии. Этапы рекурсивной триады необходимо отразить в математической модели к отчету, выполнив обоснование декомпозиции. Программу для решения каждого задания необходимо разработать методом процедурной абстракции, используя рекурсивные функции. Этапы сопроводить комментариями в коде.
Следует реализовать каждое задание в соответствии с приведенными этапами:
- изучить словесную постановку задачи, выделив при этом все виды данных;
- сформулировать математическую постановку задачи;
- выбрать метод решения задачи, если это необходимо;
- разработать графическую схему алгоритма;
- записать разработанный алгоритм на языке С++;
- разработать контрольный тест к программе;
- отладить программу;
- представить отчет по работе.
Требования к отчету.
Отчет по лабораторной работе должен соответствовать следующей структуре.
- Титульный лист.
- Словесная постановка задачи. В этом подразделе проводится полное описание задачи. Описывается суть задачи, анализ входящих в нее физических величин, область их допустимых значений, единицы их измерения, возможные ограничения, анализ условий при которых задача имеет решение (не имеет решения), анализ ожидаемых результатов.
- Математическая модель. В этом подразделе вводятся математические описания физических величин и математическое описание их взаимодействий. Цель подраздела – представить решаемую задачу в математической формулировке.
- Алгоритм решения задачи. В подразделе описывается разработка структуры алгоритма, обосновывается абстракция данных, задача разбивается на подзадачи. Схема алгоритма выполняется по ЕСПД (ГОСТ 19.003-80 и ГОСТ 19.002-80).
- Листинг программы. Подраздел должен содержать текст программы на языке программирования С++, реализованный в среде MS Visual Studio 2010.
- Контрольный тест. Подраздел содержит наборы исходных данных и полученные в ходе выполнения программы результаты.
- Выводы по лабораторной работе.
- Ответы на контрольные вопросы.
Контрольные вопросы
- Можно ли случай косвенной рекурсии свести к прямой рекурсии? Ответ обоснуйте.
- Может ли рекурсивная база содержать несколько тривиальных случаев? Ответ обоснуйте.
- Являются ли параметры, база и декомпозиция единственными для конкретной задачи? Ответ обоснуйте.
- С какой целью в задачах происходит пересмотр или корректировка выбранных параметров, выделенной базы или случая декомпозиции?
- Является ли рекурсия универсальным способом решения задач? Ответ обоснуйте.
- Почему для оценки трудоемкости рекурсивного алгоритма недостаточно одного метода подсчета вершин рекурсивного дерева?
- Выполните оценку алгоритма из Примера 3 лекции 34 методом подсчета вершин рекурсивного дерева для случая n = 6, k = 6.
