НОУ ИНТУИТ | Практикум по компьютерной геометрии. Лекция 5: Кривые и поверхности в компьютерной геометрии, I

Учитесь и получайте официальные документы БЕСПЛАТНО. Вы можете поддержать наш проект.

Регистрация Вход

Твой путь к знаниям!

Опубликован: 27.12.2010 | Доступ: свободный | Студентов: 1032 / 280 | Оценка: 5.00 / 5.00 | Длительность: 18:38:00

ISBN: 978-5-9556-0117-5

Темы: Математика, САПР

Специальности: Математик

|

Вам нравится? Нравится 14 студентам

| Поделиться |

Поддержать курс

| Скачать электронную книгу

Алгоритм де Кастелье

Алгоритм де Кастелье позволяет построить кривую Безье с помощью рекуррентного соотношения

$B_i^n=tB_{i-1}^{n-1}+(1-t)B_i^{n-1}.$

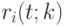Пусть даны опорные точки $p_0, \dots , p_n.$ Обозначим через r_i(t; k) кривую Безье, построенную по точкам $p_i, \dots , p_{i+k} (i + k \le n) .$

Тогда искомая кривая Безье - это кривая 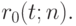r_0(t;n) . Имеем $r_i(t;0) = p_i, 0 \le i \le n.$ Выведем рекуррентные формулы для определения r_0(t; n) = r(t) исходя из начальных данных: $r_i(t; 0) \equiv p_i (0 \le i \le n) .$ Имеем

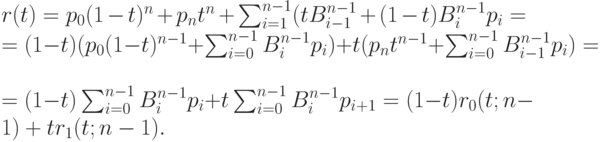
$r(t)=p_0(1-t)^n+p_nt^n+\sum_{i=1}^{n-1}(tB_{i-1}^{n-1}+(1-t)B_i^{n-1}p_i=\\ =(1-t)(p_0(1-t)^{n-1}+\sum_{i=0}^{n-1}B_i^{n-1}p_i)+t(p_nt^{n-1}+\sum_{i=0}^{n-1}B_{i-1}^{n-1}p_i)=\\ =(1-t) \sum_{i=0}^{n-1}B_i^{n-1}p_i+t \sum_{i=0}^{n-1}B_i^{n-1}p_{i+1}=(1-t)r_0(t; n-1)+tr_1(t; n-1).$

Отсюда получаем следующую рекуррентную формулу де Кастелье для вычисления кривой Безье:

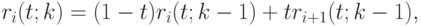$r_i(t;k)=(1-t)r_i(t; k-1)+tr_{i+1}(t;k-1),$

( 5.22)

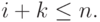
где $i + k \le n.$

По формуле (5.22), начиная от значений 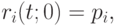r_i(t;0) = p_i, получаем последовательно значения 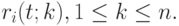$r_i (t;k), 1 \le k \le n.$ На последнем шаге вычисляем 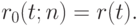r_0(t;n) = r(t) . Это и есть алгоритм де Кастелье.

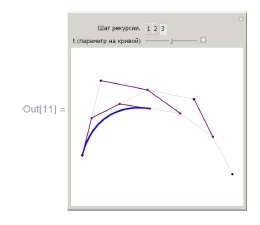
Пример 5.3.5. Алгоритм де Кастелье:

In[11]: =
        DynamicModule [ {s, r, b, t,   p} , 
             b[t_, i_, r_]   := (1 - t) b[t, i, r- 1] + tb[t, i + 1, r - 1] ; 
             b[t_, 0, 1] =  (1-t) p[0] + tp[l];   b[t_, 1, 1] =  (1-t) p[l] +tp[2]; 
             b[t_, 2,  1]  =  (1-t) p[2] + tp[3] ; p[0]  = {0.0,  0.5}; 
             p[l]  = {0.5, 2.5} ; p[2]  = {3.0, 2.0}; p[3]  = {4.0,  0.0}; 
             Manipulate[ 
                Module[{pit}, 
                   plt=ParametricPlot[b[t, 0, 3] ,   {t, 0, s} ,
                              PlotStyle -> {Blue, Thickness [0.01] }] [ [1] ] ; 
                   Which [r == 1, 
                        Graphics [{{Lighter [Gray] , Line[{p[0] ,p[l],p[2],p[3]}]}, 
                          {PointSize[0.015] , Point[{p[0] , p [1] , p [2] , p[3]}]}, 
                          {Purple, PointSize[0.015],
                            Point [{b[s,  0,  l],b[s, 1, l],b[s, 2, 1]}]}, 
                          {Purple, Thickness[0.005], Line[{p[0], b[s, 0, 1]}], 
                            Line[{p[l] , b[s, 1, 1]}] , Line [{p [2], b[s, 2, 1]}]}}, 
                            PlotRange -> {{-0.1, 4.1},   {-0.1, 2.6}}, ImageSize -> {300, 275}] , 
                       r == 2, Graphics [{{Lighter [Gray] , Line[{p[0] ,p[l],p[2],p[3]}]}, 
                          {PointSize [0.015] , Point [{p[0] ,p[l],p[2],p[3]}]}, 
                          {Lighter[Gray], 
                            Line[{{b[s, 0, l],b[s, 1, 1]},   {b[s, 1, l],b[s, 2, 1]}}]}, 
                          {Purple, PointSize[0.015], 
                            Point [{b[s, 0, 1] , b[s, 1, 1], b[s, 2, 1], b[s, 0, 2] , b[s, 1, 2]}]}, 
                          {Purple,  Thickness[0.005], 
                            Line[{{p[0], Ь[з,  0, 1]},   {p[l], b[з, 1,  1]},   {p[2], b[s, 2,  1]}, 
                             {b[s,  0,  1], b[s, 0, 2]},   {b[s,  1,  1], b[s,  1, 2]}}]}}, 
                     PlotRange -> {{-0.1,  4.1},   {-0.1, 2.6}}, ImageSize -> {300, 275}] , 
                  r == 3, Graphics [ {pit,   {Lighter [Gray] , Line[{p[0] , p [1] , p[2] , p[3] } ]} , 
                     {PointSize [0.015] , Point [{p[0] ,p[l],p[2],p[3]}]}, 
                     {Lighter[Gray], 
                       Line[{{b[s,  0, 1] , b[s, 1,  1]},   {b[s, 1,  l],b[s, 2, 1]}, 
                          {b[s, 0, 2], b[s,  1, 2]}}]}, 
                     {Purple, PointSize[0.015], 
                       Point[{b[s, 0, 1] , b[s, 1, 1] , b[s, 2, 1] , b[s, 0, 2] , b[s, 1, 2] ,
                            b[s, 0, 3]}]},   {Purple, Thickness[0.005], 
                      Line[{{p[0], b[s, 0, 1]},   {p[l], b[s, 1, 1]},   {p[2], b[s, 2, 1]}, 
                          {b[s,  0,  1], b[s,  0, 2]},   {b[s,  1,  1], b[s,  1, 2]}, 
                          {b[s,  0, 2], b[s, 0,  3]}}]}}, 
               PlotRange -> {{-0.1,  4.1},   {-0.1, 2.6}},  ImageSize -> {300, 275}]] ] , 
          {{r,  3,  "Шаг рекурсии."},   {1, 2,  3}}, 
         {{s, 0.5, "t   (параметр на кривой)"}, 0.01, 1}] ]

Пример 5.3.6. Следующий пример строит последовательность кривых Безье в форме "цветка", соседние кривые имеют только одну общую крайнюю точку. Все опорные точки расположены на двух окружностях: первая имеет радиус 1, а радиус второй управляется ползунком.

In[12]: =
             Manipulate[ 
               DynamicModule[{ptlists, img, pts2}, 
                 pts2 = 
                  Table [ If [ EvenQ[i] , 1. , r] *
                       {Sin [2 Pii *iMul/ iDiv] , Cos [2 Pi i * iMul / iDiv] } ,
                   {i,0, iLoops / 2 * LCM [iDiv, iDeg, iMul] } ] ;
                ptlists = Partition [ pts2 , iDeg + 1, iDeg]; 
                img = Graphics[{
                   Table[{If[bColor, Hue[2 *k/Length[ptlists]] , Black] , 
                       BezierCurve [ptlists [ [k] ] , SplineDegree -* iDeg] } , 
                    {k, Length[ptlists]}] }, ImageSize -" {375, 375}, Axes 4 True]] , 
          {{bColor, True, "Расцветка кривых Безье"}, {True, False}}, 
          { {iDiv, 23,
             "Количество равностоящих точек окружностей, в которых (возможно 
                 не во всех) будут располагаться все опорные точки"}, 2, 
           40, 1, ImageSize -> Tiny, Appearance -> "Labeled"} , 
         {{iDeg, 9, "Степень кривых Безье"} , 1, 11, 1, ImageSize -> Tiny, 
              Appearance -> "Labeled" } , 
          {{iMul, 7, "Шаг, с помощью которого выбираются опорные точки"},
              1, 10, 1, ImageSize->" Tiny, Appearance -> "Labeled"}, 
          {{r, .5, "Радиус второй окружности"}, 0, 1.5, .01, ImageSize -> Tiny, 
              Appearance -> "Labeled" } , 
         {{iLoops, 1, "Добавление опорных точек"}, 1, 4,1, ImageSize -> Tiny, 
              Appearance -> "Labeled" } , 
            Control Placement -> Left]

Операторная форма кривой Безье

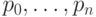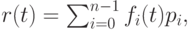Пусть даны опорные точки $p_0, \dots ,p_n$ и параметр $t \in [0,1] .$ Определим оператор правого сдвига E, действующий на кривых вида $r(t) =\sum_{i=0}^{n-1}f_i(t)p_i,$ где $f_i (t), i = 0, \dots , n - 1,$ - гладкие функции от $t \in [0,1] ,$ по формуле

$Er(t)=\sum_{i=0}^{n-1}f_i(t)p_{i+1}$

Аналогично, на кривых вида $r(t) = \sum_{i=0}^{n-1}g_i(t)p_i, t \in [0,1] ,$ определен оператор левого сдвига L:

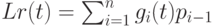
$Lr(t)=\sum_{i=1}^{n}g_i(t)p_{i-1}$

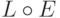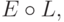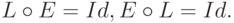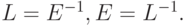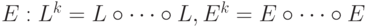Тогда на множестве кривых, для которых определен оператор $L \circ E$ или $E \circ L,$ имеем $L \circ E = Id, E \circ L = Id.$ Другими словами, $L = E^{-1}, E = L^{-1}.$ Мы будем пользоваться также степенями операторов и $E: L^k = L \circ \dots \circ L, E^k = E \circ \dots \circ E$ (где и повторяются раз), применяя их к тем кривым, для которых эти степени определены.

Кривую r(t) = p_i мы будем обозначать просто p_i.

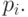
Лемма 5.1. Кривая Безье, построенная по точкам $p_0, \dots ,p_n,$ может быть задана в виде

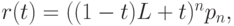( 5.23)

а также в виде

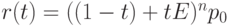( 5.24)

В операторных обозначениях алгоритм де Кастелье имеет вид

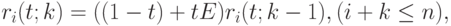
$r_i(t; k) = ( (1 -t)+ tE ) r_i(t; k-1), (i + k \le n),$

поскольку 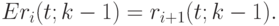$Er_i(t; k - 1) = r_{i+1}(t; k - 1) .$

В частности

$r_0(t;n)= ( (1-(t)+tE ) r_0(t;n-1),\\ r_0(t; n - 1) = (1 -t) + tE ) r_0(t; n - 2),\\ ............................................................\\ r_0(t;1) = p_0,$

что опять дает нам формулу (5.24):

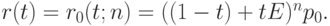
r(t) = r_0(t; n) = ( (1 -t)+ tE )^n p_0.

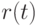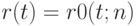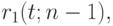Лемма 5.2. Для любого значения $t \in [0,1]$ соответствующая точка r(t) на кривой Безье r(t) = r0(t; n) делит отрезок, соединяющий точки r_0(t; n-1) и r_1(t;n-1) , в отношении 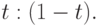t : (1-t) . Сама кривая r(t) = r_0(t;n) касается этого отрезка в точке r(t) .

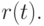
Рассмотрим две операции на кривых Безье.

Дальше >>

Авторизоваться

Практикум по компьютерной геометрии

Кривые и поверхности в компьютерной геометрии, I

Алгоритм де Кастелье

Операторная форма кривой Безье

Вопросы и ответы