Практикум по компьютерной геометрии
[+]
Опубликован: 27.12.2010 | Доступ: свободный | Студентов: 1030 / 278 | Оценка: 5.00 / 5.00 | Длительность: 18:38:00
ISBN: 978-5-9556-0117-5
Темы: Математика, САПР
Специальности: Математик
Теги: алгебра, анализ, вычисления, геометрия, программное обеспечение
Лекция 5:

Кривые и поверхности в компьютерной геометрии, I
A
|
версия для печати
< Лекция 4 || Лекция 5: 12345678 || Лекция 6 >

Сплайны

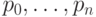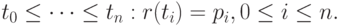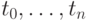Определение 5.2.1. Сплайном называется кривая, построенная по совокупности точек p_0,\dots ,p_n, которые называются характеристическими или опорными точками сплайна. Требуется, чтобы сплайн r = r(t) проходил через заданные точки p_0, \dots ,p_n при заданных значениях параметра t_0 \le \dots \le t_n: r(t_i) = p_i, 0 \le i \le n. Значения параметра t_i (0 \le i \le п) называются узловыми, а точки t_0, \dots ,t_n на оси R - узлами сплайна.

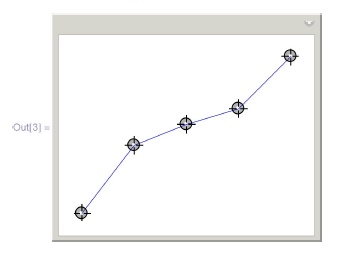
Пример 5.2.1. Ломаная линия с вершинами в точках 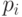p_i:

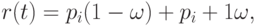
r(t) = p_i(1-\omega)+p_i+1\omega,

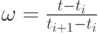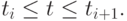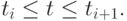
где \omega=\frac{t-t_i}{t_{i+1}-t_i} и t_i \le t \le t_{i+1}. Параметр \omega называется местным параметром на учacткe t_i \le t \le t_{i+1}.

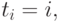Если t_i =i, то параметризация ломаной называется равномерной. В этом случае параметрическая длина 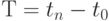Т = t_n - t_0 ломаной равна 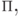п, т. е. -числу опорных точек минус 1, если все опорные точки p_0, \dots, p_n различны.

Если 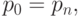p_0 = p_n, т. е. ломаная замкнута, ее параметрическая длина равна числу опорных точек (в предположении, что точки p_0, \dots , p_{n_1} различны):

In[3] = DynamicModule [ {pts } , Manipulate [
                Show[Graphics[{Blue, Thick, Line[{pts}]}]], 
                 {{pts,   {{1,  1},   {2,  2.3},   {3, 2.7},   {4, 3},   {5,  4}}}, 
                  Locator}]]

Рассмотрим основные примеры сплайнов.

Сплайн Лагранжа

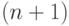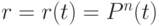Пусть дана (n+ 1) опорная точка p_i = (x_i,y_i) \in R^2, 0 \le i \le n. Требуется найти полиномиальную по t кривую r = r(t) = P^n(t) такую, что 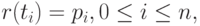r( t_i) = p_i, 0 \le i \le n, при заданных значениях параметра t_0 \le \dots \le t_n. Будем искать решение этой задачи в виде

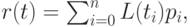
r(t)=\sum_{i=0}^{n}L(t_i)p_i,

где

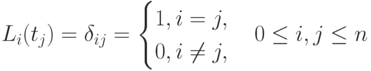
L_i(t_j)= \delta_{ij}= \begin{cases} 1, i=j,\\ 0, i \ne j, \end{cases} 0 \le i,j \le n

Таким свойствами обладают многочлены

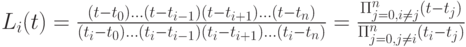
L_i(t)=\frac{(t-t_0) \dots (t-t_{i-1})(t-t_{i+1})\dots (t-t_n)}{(t_i-t_0) \dots (t_i-t_{i-1})(t_i-t_{i+1}) \dots (t_i-t_n)}=\frac{\Pi_{j=0, i \ne j}^{n}(t-t_j)}{\Pi_{j=0, j \ne i}^{n}(t_i-t_j)}

С их помощью получаем сплайн Лагранжа:

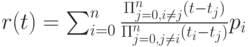
r(t)=\sum_{i=0}^{n}\frac{\Pi_{j=0, i \ne j}^{n}(t-t_j)}{\Pi_{j=0, j \ne i}^{n}(t_i-t_j)}p_i

или

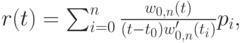
r(t)=\sum_{i=0}^{n}\frac{w_{0,n}(t)}{(t-t_0)w_{0,n}'(t_i)}p_i,

где

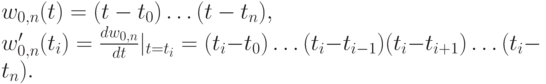
w_{0,n}(t) = (t-t_0) \dots (t-t_n),\\ w_{0 ,n}' (t_i ) = \frac{dw_{0,n}}{ dt }|_{t=t_i}= ( t_i - t_0) \dots ( t_i - t_{i-1})( t_i - t_{i+1}) \dots ( t_i - t_n).

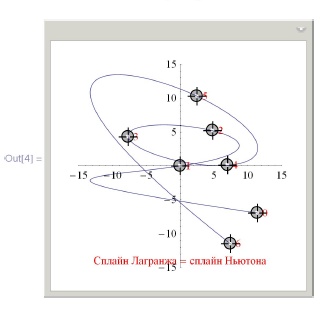
Главный недостаток сплайнов Лагранжа состоит в том, что между двумя соседними опорными точками они могут образовывать петли. Такие петли, не обусловленные расположением опорных точек, называются необоснованными петлями и являются существенным недостатком сплайна, не позволяющим применять данный сплайн для большинства приложений компьютерной геометрии.

Еще один существенный недостаток сплайнов Лагранжа состоит в том, что они могут выходить за пределы выпуклой оболочки своих опорных точек, причем довольно значительно.

Эти недостатки - цена за бесконечную гладкость сплайна на всей области определения параметра. Поэтому в компьютерной геометрии чаще всего пользуются не гладкими, а кусочно-гладкими сплайнами, о которых пойдет речь ниже.

Пример 5.2.2. Сплайн Лагранжа с возможностью управления опорными точками:

In[4] :=
         DynamicModule [ {pts , ptsO , L, t, p, n = 6, tt} , 
           ptsO ={{6.0, 0.0}, {0.0, 0.0}, {4.8, 5.2}, {0.3, 5.5}, {9.0, 3.0},
              {4.3, 8.2} , {10.0, 6.0}} ;
           tt= {1.0, 2.0, 3.0, 4.0, 5.0, 6.0, 7.0}; 
           p[i_, s_] : =
             Apply [Times , (s - tt [ [tt] ] ) & /@ Drop [Range [n + 1] , {i + 1} ] ] ; 
           L = Table [p [i , t] / p [i , tt [ [i + 1] ] ] , {i , 0 , n} ] ; 
           Manipulate[ 
             Show[{ParametricPlot[L.pts, {t, tt[[l]], tt[[-l]]}, 
                  PlotRange -> {{-15, 15}, {-15, 15}}], 
               Graphics [{Red, Text [ToString [tt - 1] , pts [ [#] ] +{1.2, 0}] &/@ 
                   Range[n + 1] , Text["Сплайн Лагранжа = сплайн Ньютона", 
                   {8, -14}]}]}], {{pts, ptsO}, Locator}]]

Сплайн Ньютона

Сплайн Ньютона представляет собой тот же самый сплайн Лагранжа, но в другой форме, удобной для перевычисления сплайна в случае добавления новых опорных точек.

А именно, сплайн Ньютона записывается в виде

r(t) = a_0 + a_1(t - t_0) + a_2(t - t_0)(t - t_1) + \dots + a_n(t - t_0) \dots (t - t_{n_1}),

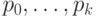где векторные коэффициенты a_0, \dots , a_n ищутся из условий прохождения сплайна через точки p_0, \dots , p_n. При этом точки p_0, \dots , p_k полностью определяют коэффициенты a_0, \doys , a_k, 0 \le k \le n, с помощью системы уравнений

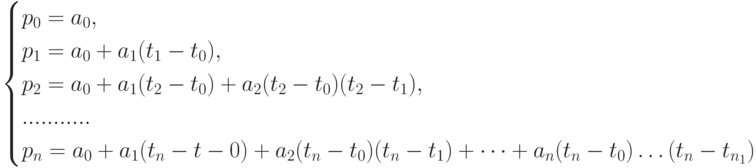
\begin{cases} p_0 = a_0,\\ p_1=a_0+a_1(t_1-t_0),\\ p_2 = a_0 + a_1(t_2 - t_0) + a_2(t_2 - t_0)(t_2 - t_1),\\ ...........\\ p_n = a_0 + a_1(t_n - t-0) + a_2(t_n - t_0)(t_n - t_1) + \dots +a_n(t_n-t_0) \dots (t_n-t_{n_1}) \end{cases}

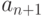Эта система решается за один проход, так как матрица системы является нижнетреугольной. Из первых 1 \le k \le n + 1 уравнений определяются первые k неизвестные a_0, \dots , a_{k_1}. Поэтому если мы добавим еще одну точку p_{n+1}, нам будет нужно лишь определить еще один коэффициент a_{n+1} из еще одного, добавленного уравнения. Коэффициенты a_0, \dots ,a_n при этом останутся прежними.

Задача 5.2.1. Написать программу для сплайна Ньютона с возможностью добавлять точку.

Сплайн Эрмита

Сплайны Эрмита предназначены для соединения двух заданных кривых новой кривой, полиномиальной по параметру, так, чтобы получившаяся совокупная кривая имела заданную степень гладкости в точках стыковки. Отсюда следует, что сплайн Эрмита задается двумя своими крайними точками и заданным числом m производных радиус-вектора в каждой из крайних точек. Сплайн Эрмита имеет вид полинома степени 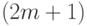(2m + 1) по t. Степень полинома называется порядком сплайна. 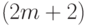При этом (2m + 2) векторных коэффициентов этого полинома определяются из системы (2m+ 2) уравнений ( 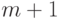m + 1 условие для каждой из двух крайних точек).

Сплайн Эрмита может быть определен формулой

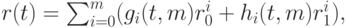r(t)=\sum_{i=0}^m(g_i(t,m)r_0^i+h_i(t,m)r_1^i), ( 5.1)

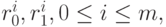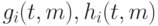где r_0^i, r_1^i, 0 \le i \le m, - заданные значения радиус-вектора кривой и его m производных на концах, а g_i(t, m), h_i(t, m) даются формулами

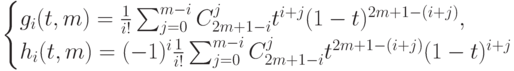\begin{cases} g_i(t,m)=\frac{1}{i!}\sum_{j=0}^{m-i}C_{2m+1-i}^{j}t^{i+j}(1-t)^{2m+1-(i+j)},\\ h_i(t,m)=(-1)^i \frac{1}{i!}\sum_{j=0}^{m-i}C_{2m+1-i}^{j}t^{2m+1-(i+j)}(1-t)^{i+j} \end{cases} ( 5.2)

Задача 5.2.2. Написать программу для сплайна Эрмита с возможностью добавлять точку. Запрограммировав сплайны Эрмита, проверить на Mathematica, что производные радиус-вектора на концах сплайна равны заданным значениям.

Дальше >>
< Лекция 4 || Лекция 5: 12345678 || Лекция 6 >

Вопросы и ответы

вопросов: 0