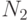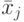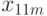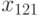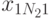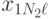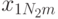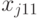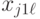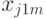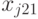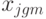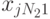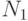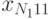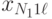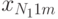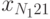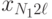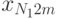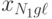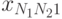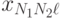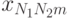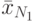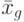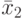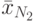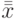|
Добрый день. Я приступила сегодня к самостоятельному изучению курса "Моделирование систем". Хочу понять - необходимо ли отсылать мои решения практических заданий на сайт, (и если да - то где найти волшебную кнопку "Загрузить...") или практические задания остаются полностью на моей совести? (никто не проверяет, и отчётности по ним я предоставлять не обязана?) P.S.: тьютора я не брала |
Введение в дисперсионный анализ
3. Двухфакторный дисперсионный анализ
При двухфакторном анализе исследуется влияние двух качественных факторов  и
и  на отклик
на отклик  . В этом случае дисперсионный анализ основывается на результатах эксперимента, проводимого на различных уровнях каждого из факторов. Предполагается, что взаимосвязь между факторами отсутствует. В эксперименте с повторными опытами результаты могут быть представлены в виде табл. 8.2.
. В этом случае дисперсионный анализ основывается на результатах эксперимента, проводимого на различных уровнях каждого из факторов. Предполагается, что взаимосвязь между факторами отсутствует. В эксперименте с повторными опытами результаты могут быть представлены в виде табл. 8.2.
Результаты обработки данных табл. 8.2 принято сводить в таблицу следующего вида:
| Сводная таблица данных | |||||||
| Источник изменчивости | Сумма квадратов | Число степеней свободы | Средняя сумма квадратов | Расчетная статистика | |||
Фактор 
|
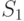 |
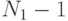 |
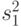 |
 |
|||
Фактор 
|
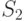 |
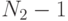 |
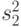 |
 |
|||
| Ошибки | 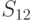 |
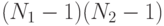 |
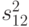 |
 |
|||
| Сумма | 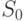 |
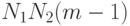 |
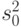 |
||||
Вычислительная схема двухфакторного дисперсионного анализа
- Общее среднее всех
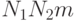 опытов по всем
опытов по всем  сочетаниям уровней:
сочетаниям уровней: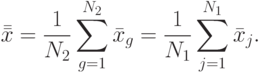
( 8.19) - Общая сумма квадратов отклонений наблюдений от общего среднего:
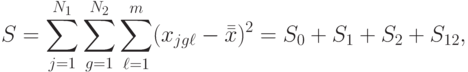
( 8.20) где:
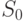 — сумма квадратов отклонений внутри серий (табл. 8.3):
— сумма квадратов отклонений внутри серий (табл. 8.3):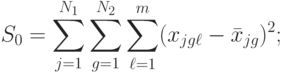
( 8.21) 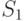 — сумма квадратов отклонений между строками (табл. 8.3):
— сумма квадратов отклонений между строками (табл. 8.3):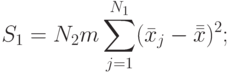
( 8.22) 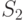 — сумма квадратов отклонений между столбцами (табл. 8.3):
— сумма квадратов отклонений между столбцами (табл. 8.3):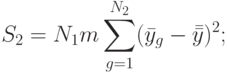
( 8.23) 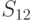 — сумма квадратов отклонений между сериями (табл. 8.3):
— сумма квадратов отклонений между сериями (табл. 8.3):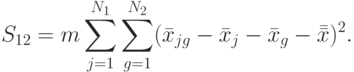
( 8.24)
Расчет дисперсий с соответствующим числом степеней свободы
3.
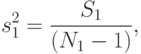 |
( 8.25) |
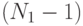 — число степеней свободы.
— число степеней свободы.
4.
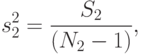 |
( 8.26) |
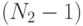 — число степеней свободы.
— число степеней свободы.
5.
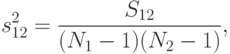 |
( 8.27) |
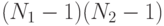 — число степеней свободы.
— число степеней свободы.
6.
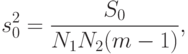 |
( 8.28) |
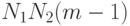 — число степеней свободы.
— число степеней свободы.
Расчет влияний факторов и их взаимодействий на отклик
Влияние факторов  и
и  признается значимым, если
признается значимым, если
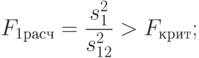 |
( 8.29) |
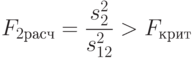 |
( 8.30) |
при заданном уровне значимости  и соответствующем числе степеней свободы из формул (8.25), (8.26), (8.27).
и соответствующем числе степеней свободы из формул (8.25), (8.26), (8.27).
Влияние взаимодействия факторов  ,
,  будет значимым, если
будет значимым, если
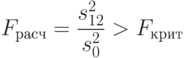 |
( 8.31) |
при заданном уровне значимости  и соответствующем числе степеней свободы из формул (8.27), (8.28).
и соответствующем числе степеней свободы из формул (8.27), (8.28).

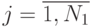 )
)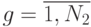 )
)