|
Добрый день. Я приступила сегодня к самостоятельному изучению курса "Моделирование систем". Хочу понять - необходимо ли отсылать мои решения практических заданий на сайт, (и если да - то где найти волшебную кнопку "Загрузить...") или практические задания остаются полностью на моей совести? (никто не проверяет, и отчётности по ним я предоставлять не обязана?) P.S.: тьютора я не брала |
Введение в дисперсионный анализ
Теоретическая часть
Объектом исследования дисперсионного анализа являются стохастические связи между откликом (реакцией) и факторами, когда последние носят не количественный, а качественный характер [13].
Дисперсионный анализ применяют, чтобы установить, оказывает ли существенное влияние некоторый качественный фактор  , который имеет
, который имеет 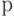 уровней
уровней 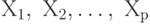 на изучаемую величину
на изучаемую величину  .
.
Основная идея дисперсионного анализа состоит в сравнении "факторной дисперсии", порождаемой воздействием конкретного фактора, и "остаточной дисперсии", обусловленной случайными причинами [6]. Если различие между этими дисперсиями значимо, то фактор оказывает существенное влияние на  ; в этом случае средние величины наблюдаемых значений на каждом уровне (групповые средние) различаются также значимо. Если уже установлено, что фактор существенно влияет на
; в этом случае средние величины наблюдаемых значений на каждом уровне (групповые средние) различаются также значимо. Если уже установлено, что фактор существенно влияет на  , а требуется выяснить, какой из уровней оказывает наибольшее воздействие, то сравнение средних дополнительно производят попарно.
, а требуется выяснить, какой из уровней оказывает наибольшее воздействие, то сравнение средних дополнительно производят попарно.
В зависимости от числа анализируемых факторов различают однофакторный, двухфакторный и т. д. дисперсионные анализы [13]. В работе будут рассмотрены однофакторный и двухфакторный дисперсионные анализы.
1. Однофакторный дисперсионный анализ
Однофакторный дисперсионный анализ может быть использован для выявления наиболее существенных связей между переменными при качественном исследовании объектов различной природы.
При однофакторном анализе проверяется действие одного фактора  на выходную переменную
на выходную переменную  по результатам
по результатам  экспериментов с
экспериментов с  дублирующими опытами. Общее количество экспериментов равно
дублирующими опытами. Общее количество экспериментов равно  . Результаты эксперимента
. Результаты эксперимента  наблюдений могут быть сведены в таблицу (табл. 8.1), где
наблюдений могут быть сведены в таблицу (табл. 8.1), где 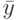 означает среднее значение выходной переменной в одной серии дублирующих опытов [3]. Количество
означает среднее значение выходной переменной в одной серии дублирующих опытов [3]. Количество  экспериментов соответствует возможным уровням фактора
экспериментов соответствует возможным уровням фактора  . Под уровнем фактора понимаются возможные его качественные значения. Поэтому если производится
. Под уровнем фактора понимаются возможные его качественные значения. Поэтому если производится  экспериментов, то это означает, что рассматриваются
экспериментов, то это означает, что рассматриваются  возможных уровней фактора, которые оказывают влияние на значение выходной переменной
возможных уровней фактора, которые оказывают влияние на значение выходной переменной  системы или объекта исследования.
системы или объекта исследования.
| Результаты наблюдений однофакторного эксперимента | |||||||
| Номер уровня фактора | Дублирующие опыты | Среднее дублирующего опыта | |||||
| 1 | 2 | ... | 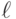 |
... |  |
||
| 1 |  |
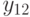 |
... | 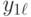 |
... |  |
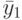 |
| 2 | 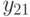 |
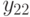 |
... | 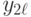 |
... | 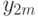 |
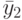 |
| ... | ... | ... | ... | ... | ... | ... | ... |
 |
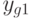 |
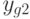 |
... | 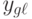 |
... |  |
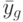 |
 |
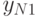 |
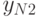 |
... | 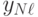 |
... |  |
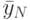 |
| ... | ... | ... | ... | ... | ... | ... | ... |
Среднее серий из повторных (дублирующих) опытов для каждого уровня фактора определяется по формуле
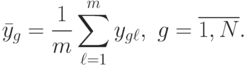 |
( 8.1) |
Общее среднее всех  наблюдений по всем
наблюдений по всем  уровням фактора определяется по формуле
уровням фактора определяется по формуле
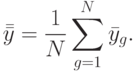 |
( 8.2) |
Общая сумма  квадратов отклонений отдельных наблюдений
квадратов отклонений отдельных наблюдений 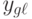 от общего среднего
от общего среднего 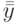 вычисляется по формуле
вычисляется по формуле
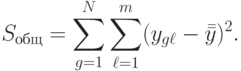 |
( 8.3) |
Формулу (8.3) можно преобразовать к виду
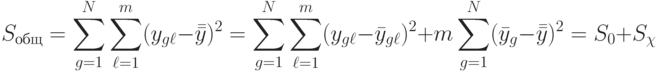 |
( 8.4) |
где:
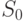 — сумма квадратов отклонений внутри серий, т. е. сумма квадратов разностей между отдельными наблюдениями y_{g\ell0}(\ell=\overline{1,m}) и средним \bar y_g соответствующей серии (g=\overline{1,N});
— сумма квадратов отклонений внутри серий, т. е. сумма квадратов разностей между отдельными наблюдениями y_{g\ell0}(\ell=\overline{1,m}) и средним \bar y_g соответствующей серии (g=\overline{1,N});
 — сумма квадратов отклонений между сериями или рассеивание по уровням, т. е. взвешенная с учетом числа наблюдений в каждой серии
— сумма квадратов отклонений между сериями или рассеивание по уровням, т. е. взвешенная с учетом числа наблюдений в каждой серии 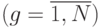 сумма квадратов между средними
сумма квадратов между средними 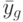 отдельных серий и общим средним
отдельных серий и общим средним 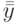 по всей совокупности наблюдений.
по всей совокупности наблюдений.
 характеризует влияние фактора и случайных причин.
характеризует влияние фактора и случайных причин. 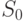 отражает влияние случайных причин.
отражает влияние случайных причин.  характеризует воздействие фактора.
характеризует воздействие фактора.
Если в результате анализа оказалось, что влияние качественного фактора на выходную переменную отсутствует, тогда средние 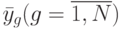 серий имеют одинаковую оценку математического ожидания и дисперсию
серий имеют одинаковую оценку математического ожидания и дисперсию  и все
и все  наблюдений можно рассматривать как выборку из одной и той же совокупности, распределенной по нормальному закону.
наблюдений можно рассматривать как выборку из одной и той же совокупности, распределенной по нормальному закону.
Несмещенная общая оценка дисперсии 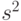 по всем
по всем  наблюдениям определяется по формуле
наблюдениям определяется по формуле
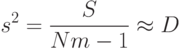 |
( 8.5) |
с числом степеней свободы
 |
( 8.6) |
Выборочная дисперсия 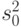 внутри серий (
внутри серий ( 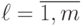 ) дублирующих опытов определяется по формуле
) дублирующих опытов определяется по формуле
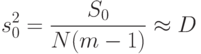 |
( 8.7) |
с числом степеней свободы
 |
( 8.8) |
Выборочная дисперсия 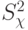 внутри серий (
внутри серий ( 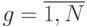 ) по уровням определяется по формуле
) по уровням определяется по формуле
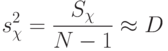 |
( 8.9) |
с числом степеней свободы
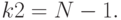 |
( 8.10) |
Проверка значимости влияния фактора производится с помощью критерия Фишера при заданном уровне значимости  (% или относительная величина) по формуле
(% или относительная величина) по формуле
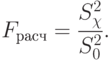 |
( 8.11) |
Если вычисленное значение по результатам наблюдений  окажется больше значения теоретической величины критерия Фишера
окажется больше значения теоретической величины критерия Фишера  при заданном уровне значимости и соответствующих степенях свободы (8.8), (8.10), то влияние фактора признается значимым.
при заданном уровне значимости и соответствующих степенях свободы (8.8), (8.10), то влияние фактора признается значимым.
Критическое значение критерия Фишера можно определить по таблицам, которые составлены для различных уровней значимости и приводятся во многих учебниках по теории вероятности и математической статистике. Например, если  , то
, то 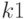 — число степеней свободы дисперсии
— число степеней свободы дисперсии 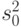 — берется из верхней строки таблицы, а
— берется из верхней строки таблицы, а 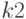 — число степеней свободы меньшей дисперсии
— число степеней свободы меньшей дисперсии 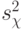 — из левого столбца таблицы. Критическое значение критерия Фишера можно определить также с помощью встроенных функций пакета Statistics Toolbox системы MATLAB.
— из левого столбца таблицы. Критическое значение критерия Фишера можно определить также с помощью встроенных функций пакета Statistics Toolbox системы MATLAB.
2. Однофакторный дисперсионный анализ с неодинаковым числом испытаний на различных уровнях
Выше рассматривался однофакторный дисперсионный анализ с одинаковым числом испытаний на различных уровнях данного одного фактора. Рассмотрим случай однофакторного дисперсионного анализа, когда число испытаний на различных уровнях различно [6]. Пусть произведено 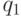 испытаний на первом уровне (
испытаний на первом уровне ( 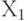 ),
), 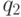 испытаний — на втором уровне
испытаний — на втором уровне 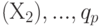 испытаний – на уровне
испытаний – на уровне 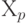 . В этом случае общую сумму квадратов отклонений находят по формуле
. В этом случае общую сумму квадратов отклонений находят по формуле
![S_{общ}=[P_1+P_2+...+P_p]-\frac{(R_1+R_2+...+R_p)^2}{n},](/sites/default/files/tex_cache/50d6cdc90fc6a9a168aaec65c3f5b9a8.png) |
( 8.12) |
где:
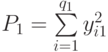 — сумма квадратов наблюдавшихся значений отклика на уровне
— сумма квадратов наблюдавшихся значений отклика на уровне 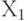 ;
;
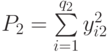 — сумма квадратов наблюдавшихся значений отклика на уровне
— сумма квадратов наблюдавшихся значений отклика на уровне 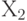 ;
;
…………………………………………………………………
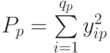 — сумма квадратов наблюдавшихся значений отклика на уровне
— сумма квадратов наблюдавшихся значений отклика на уровне 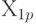 ;
;
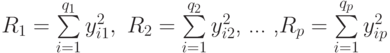 — суммы наблюдавшихся значений отклика на уровнях
— суммы наблюдавшихся значений отклика на уровнях 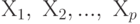 ;
;
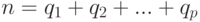 — общее число испытаний (общий объем выборки).
— общее число испытаний (общий объем выборки).
Факторную сумму квадратов отклонений находят по формуле
![S_{факт}=\left[\left(\frac{R_1^2}{q_1}\right)+\left(\frac{R_2^2}{q_2}\right)+...+\left(\frac{R_p^2}{q_p}\right)\right]-\left[\frac{(R_1+R_2+R_p)^2}{n}\right].](/sites/default/files/tex_cache/e55ad38b1f1b12b506dd36e019bf3ef4.png) |
( 8.13) |
Здесь по-прежнему выполняется соотношение  .
.
Поэтому остаточную сумму квадратов можно определить в виде
 |
( 8.14) |
Факторная  и остаточная
и остаточная 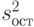 дисперсии вычисляются по формулам
дисперсии вычисляются по формулам
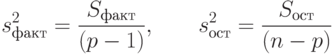 |
( 8.15) |
Где:  — число степеней свободы факторной дисперсии; (8.16)
— число степеней свободы факторной дисперсии; (8.16)
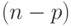 — число степеней свободы остаточной дисперсии; (8.17)
— число степеней свободы остаточной дисперсии; (8.17)
 — число факторов.
— число факторов.
Проверка значимости влияния фактора производится с помощью критерия Фишера при заданном уровне значимости  (процент или относительная величина) по формуле
(процент или относительная величина) по формуле
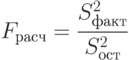 |
( 8.18) |
Если вычисленное значение по результатам наблюдений  окажется больше значения
окажется больше значения  теоретической величины критерия Фишера при заданном уровне значимости и соответствующих степенях свободы (8.16), (8.17), то влияние фактора признается значимым. Соответственно, нулевая гипотеза о равенстве групповых средних отвергается.
теоретической величины критерия Фишера при заданном уровне значимости и соответствующих степенях свободы (8.16), (8.17), то влияние фактора признается значимым. Соответственно, нулевая гипотеза о равенстве групповых средних отвергается.
