|
Добрый день. Я приступила сегодня к самостоятельному изучению курса "Моделирование систем". Хочу понять - необходимо ли отсылать мои решения практических заданий на сайт, (и если да - то где найти волшебную кнопку "Загрузить...") или практические задания остаются полностью на моей совести? (никто не проверяет, и отчётности по ним я предоставлять не обязана?) P.S.: тьютора я не брала |
Метод максимального правдоподобия точечной оценки неизвестных параметров вероятностных распределений
Теоретическая часть
Метод максимального или наибольшего правдоподобия предложен Р. Фишером [6, 13]. С помощью этого метода производится точечная оценка неизвестных параметров априорно известного закона распределения случайной величины.
Рассмотрим сначала суть метода при оценке параметров дискретного распределения случайной величины [6].
Обозначим вероятность того, что в результате испытания величина  примет значение
примет значение 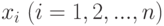 , через
, через 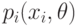 .
.
Определение. Функцией правдоподобия случайной дискретной величины  называют функцию аргумента
называют функцию аргумента  :
:
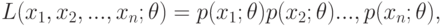 |
( 7.1) |
где 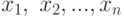 — фиксированные числа, полученные при измерении случайной величины
— фиксированные числа, полученные при измерении случайной величины  .
.
В качестве точечной оценки параметра  принимают такое его значение
принимают такое его значение 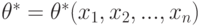 , при котором функция правдоподобия достигает максимума. Оценку
, при котором функция правдоподобия достигает максимума. Оценку  называют оценкой максимального правдоподобия.
называют оценкой максимального правдоподобия.
Для упрощения расчетов в рассмотрение вводится логарифм функции правдоподобия 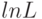 , которую называют логарифмической функцией правдоподобия. Функции
, которую называют логарифмической функцией правдоподобия. Функции  и
и 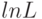 достигают максимума при одном и том же значении своего аргумента, поэтому вместо отыскания максимума функции
достигают максимума при одном и том же значении своего аргумента, поэтому вместо отыскания максимума функции  ищут максимум функции
ищут максимум функции 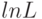 . Записывая необходимое условие экстремума функции правдоподобия в случае скалярного параметра, получаем уравнения правдоподобия
. Записывая необходимое условие экстремума функции правдоподобия в случае скалярного параметра, получаем уравнения правдоподобия
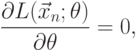 |
( 7.2) |
или
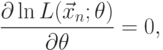 |
( 7.3) |
где 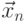 — заданная выборка случайных величин.
— заданная выборка случайных величин.
Уравнение правдоподобия (7.3) с логарифмической функцией, как правило, более простое относительно функции правдоподобия (7.2).
Если распределение случайной величины  зависит от вектора параметров
зависит от вектора параметров 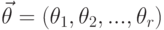 , то уравнение (7.3) заменяется системой уравнений
, то уравнение (7.3) заменяется системой уравнений
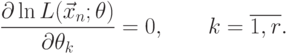 |
( 7.4) |
Именно уравнения (7.3) и (7.4) принято называть уравнениями правдоподобия [13]. Во многих случаях решение системы (7.4), являющейся, как правило, нелинейной, приходится искать численными методами.
Рассмотрим применение метода максимального правдоподобия для оценки параметров непрерывного распределения случайных величин генеральной совокупности  .
.
Пусть  — непрерывная случайная величина, которая в результате
— непрерывная случайная величина, которая в результате  испытаний приняла значения
испытаний приняла значения 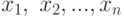 . Предполагается, что вид плотности распределения
. Предполагается, что вид плотности распределения  задан, но неизвестен параметр
задан, но неизвестен параметр  , которым определяется эта функция.
, которым определяется эта функция.
Определение. Функцией правдоподобия непрерывной случайной величины  называют функцию аргумента
называют функцию аргумента 
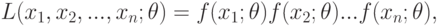 |
( 7.5) |
где 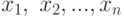 — фиксированные числа.
— фиксированные числа.
Оценку максимального правдоподобия неизвестного параметра  распределения непрерывной случайной величины ищут так же, как в случае дискретной величины.
распределения непрерывной случайной величины ищут так же, как в случае дискретной величины.
Замечание. Если плотность распределения непрерывной случайной величины  определяется двумя неизвестными параметрами
определяется двумя неизвестными параметрами 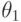 и
и 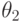 , то функция правдоподобия является функцией двух независимых аргументов
, то функция правдоподобия является функцией двух независимых аргументов 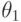 и
и 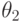 :
:
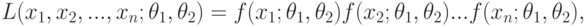 |
( 7.6) |
Как для дискретных распределений, так и для непрерывных точку максимума логарифмической функции распределения 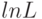 аргумента
аргумента  можно искать через необходимое условие экстремума:
можно искать через необходимое условие экстремума:
- найти производную
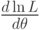 ;
; - приравнять производную нулю и найти критическую точку — корень полученного уравнения (его называют уравнением правдоподобия);
- найти вторую производную
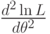 ; если вторая производная при
; если вторая производная при 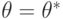 отрицательна, то
отрицательна, то  – точка максимума [6].
– точка максимума [6].
Найденную точку максимума  принимают в качестве оценки максимального правдоподобия параметра
принимают в качестве оценки максимального правдоподобия параметра  .
.
Метод максимального правдоподобия имеет ряд достоинств: его оценки, вообще говоря, состоятельны (но они могут быть смещенными), распределены асимптотически нормально (при больших значениях  приближенно нормально) и имеют наименьшую дисперсию по сравнению с другими асимптотически нормальными оценками; если для оцениваемого параметра
приближенно нормально) и имеют наименьшую дисперсию по сравнению с другими асимптотически нормальными оценками; если для оцениваемого параметра  существует эффективная оценка
существует эффективная оценка  , то уравнение правдоподобия имеет единственное решение
, то уравнение правдоподобия имеет единственное решение  ; этот метод наиболее полно использует данные выборки об оцениваемом параметре, поэтому он особенно полезен в случае малых выборок. Недостаток метода состоит в том, что он часто требует сложных вычислений.
; этот метод наиболее полно использует данные выборки об оцениваемом параметре, поэтому он особенно полезен в случае малых выборок. Недостаток метода состоит в том, что он часто требует сложных вычислений.
Практическая часть
1. Оценка параметра экспоненциального распределения
Рассматривается пример поиска методом максимального правдоподобия оценки параметра  экспоненциального распределения случайной величины, для которой функция плотности имеет вид
экспоненциального распределения случайной величины, для которой функция плотности имеет вид
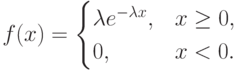 |
( 7.7) |
К характеристикам экспоненциального распределения относятся математическое ожидание ![M[X]](/sites/default/files/tex_cache/3c68892dcbe5fa2f2bec99c61aebef95.png) и дисперсия
и дисперсия ![D[X]](/sites/default/files/tex_cache/170537c0284a060429415faa254a8407.png) :
:
![M[X]=\frac{1}{\lambda},](/sites/default/files/tex_cache/fcafad1f5dd710e1f436d7162c051f12.png) |
( 7.8) |
![D[X]=\frac{1}{\lambda^2}.](/sites/default/files/tex_cache/75ae0b68f47752031afcf0251fa5bf00.png) |
( 7.9) |
Замечание. Во встроенных функциях MATLAB параметром экспоненциального распределения является математическое ожидание случайной величины.
Возможная программная реализация точечной оценки параметра экспоненциального распределения:
clear,clc,close all
%%% Проверка на закрытие диалоговых окон
try
global h11
close(h11);
end
try
global n11
close(n11);
end
try
global v11
close(v11)
end
%% ВВОД ТЕОРЕТИЧЕСКОГО ПАРАМЕТРА РАСПРЕДЕЛЕНИЯ
options.Resize = 'on';
options.WindowStyle = 'modal'; %%'normal';
options.Interpreter = 'tex';
P1 = inputdlg({'\bfВвод параметра:......................................................'},...
sprintf('Теоретическая величина параметра'),1,{'1.23'},options);
%% ПРЕОБРАЗОВАНИЕ К СТРОКОВОЙ ПЕРЕМЕННОЙ
P2 = char(P1);
%% ПРЕОБРАЗОВАНИЕ К ЧИСЛУ С ДВОЙНОЙ ТОЧНОСТЬЮ
P0 = str2num(P2);
%% КОНТРОЛЬ ВВОДА ПАРАМЕТРА
if isempty(P0)
h11 = errordlg('Параметр должен быть действительным положительным числом!','Ошибка ввода');
return
end
%% КОНТРОЛЬ ВВОДА ПАРАМЕТРА
global h11
if P0 <= 0 | ~isreal(P0) | ~isfinite(P0)
h11 = errordlg('Параметр должен быть конечным действительным положительным числом!','Ошибка ввода');
return
end
% ВВОД ЧИСЛА ПРОГОНОВ ПРОГРАММЫ
n1 = inputdlg({'\bfВвод числа прогонов программы..........................'},...
'Число прогонов программы',1,{'10'}, options);
% ПРЕОБРАЗОВАНИЕ К ЧИСЛОВОЙ ПЕРЕМЕННОЙ
n = str2num(char(n1));
%% Контроль ввода цифр
if isempty(n)
global n11
n11 = errordlg('Число прогонов программы должно быть целым положительным числом!', 'Ошибка ввода');
return
end
if ~isreal(n) | ~isfinite(n)
global n11
n11 = errordlg('Число прогонов программы должно быть целым положительным числом!', 'Ошибка ввода');
return
end
%% Контроль целого положительного числа циклов
if n <= 0 | n ~= round(n)
global n11
n11 = errordlg('Число прогонов программы должно быть целым положительным числом!', 'Ошибка ввода');
return
end
% ВВОД ЧИСЛА ИЗМЕРЕНИЙ СЛУЧАЙНОЙ ВЕЛИЧИНЫ
v1 = inputdlg({'\bfВвод числа измерений случайной величины...................................'},...
'Число измерений случайной величины',1,{'1234'}, options);
% ПРЕОБРАЗОВАНИЕ К ЧИСЛОВОЙ ПЕРЕМЕННОЙ
v = str2num(char(v1));
if isempty(v)
global v11
v11 = errordlg('Число измерений должно быть положительным целым числом!','Ошибка ввода');
return
end
if ~isreal(v) | ~isfinite(v)
global v11
v11 = errordlg('Число измерений должно быть положительным целым числом!','Ошибка ввода');
return
end
% КОНТРОЛЬ ЦЕЛОГО ЧИСЛА ИЗМЕРЕНИЙ
% СЛУЧАЙНОЙ ВЕЛИЧИНЫ
if v <= 0 | v ~= round(v)
global v11
v11 = errordlg('Число измерений должно быть положительным целым числом!','Ошибка ввода');
return
end
syms m
k = 0;
%% ЦИКЛ ЗАДАННОГО ЧИСЛА ПРОГОНОВ ПРОГРАММЫ
for I = 1:n
k=k+1;
%% ФОРМИРОВАНИЕ ЧИСЛА ИЗМЕРЕНИЙ СЛУЧАЙНОЙ ВЕЛИЧИНЫ
t = exprnd(1/P0,v,1);
%% ФОРМИРОВАНИЕ ФУНКЦИИ МАКСИМАЛЬНОГО
%% ПРАВДОПОДОБИЯ
L = m^(length(t))*exp(-m*sum(t));
%% ЛОГАРИФМИЧЕСКАЯ ФУНКЦИЯ МАКСИМАЛЬНОГО
%% ПРАВДОПОДОБИЯ
Lg = log(L);
%% ДИФФЕРЕНЦИРОВАНИЕ
dLg = diff(Lg,m);
%% ПРЕОБРАЗОВАНИЕ СИМВОЛЬНОЙ ПЕРЕМЕННОЙ К СТРОКОВОЙ
dLg = char(dLg);
%% РЕШЕНИЕ УРАВНЕНИЯ ОТНОСИТЕЛЬНО ОЦЕНИВАЕМОГО
%% ПАРАМЕТРА
as1(k) = double(solve(dLg));
%% УСРЕДНЕНИЕ ОЦЕНИВАЕМОГО ПАРАМЕТРА
as(k) = mean(as1);
end
%% ОКОНЧАНИЕ ЦИКЛА ЗАДАННОГО ЧИСЛА ПРОГОНОВ ПРОГРАММЫ
mcp = mean(as);
%% ВЫВОД РЕЗУЛЬТАТОВ В КОМАНДНОЕ ОКНО
fprintf('\n\t%s%g\n \t%s%g\n','Теоретический параметр: ',P0,...
'Оценка параметра: ', mcp)
fprintf('\tОтносительная погрешность: %g%s\n',abs(P0-mcp)/P0*100,'%')
%% ГРАФИЧЕСКИЕ ПОСТРОЕНИЯ
figure(1)
%% set(gcf,'position',[a(3)/90,a(3)/20,a(3)/2.1,a(4)/2])
plot(1:n,as1,'r:','linew',2),grid off,hold on,
plot(1:n,as,'linew',2),
title(sprintf('%s%g','\bfТеоретический параметр\fontsize{12} \lambda\fontsize{10} = ',P0))
xlabel('\bf Количество циклов'),
ylabel('\bf Эмпирический параметр\fontsize{14} \lambda'),
legend('\bf Измеряемая величина\fontsize{12} \lambda',...
'\bf Средняя величина\fontsize{12} \lambda'),
set(gcf,'color','w')
%% ПОСТРОЕНИЕ ТЕОРЕТИЧЕСКОЙ И ЭМПИРИЧЕСКОЙ
%% ФУНКЦИИ ПЛОТНОСТИ
t = 0 : 0.1 : 4;
y1 = P0*exp(-P0*t); %exppdf(t,1/P0); % встроенная функция
y2 = mcp*exp(-mcp*t); %exppdf(t,1/mcp);
figure(2)
plot(t, y1, 'r', 'linew',2),
hold on
plot(t, y2, 'bo', 'linew',2)
grid off
legend('\bf Теоретическая функция плотности (PDF)',...
'\bf Эмпирическая функция плотности'),
text(t(end)/3,2/3*max(max([y1,y2])),['\bf',...
sprintf('Теоретический параметр: %g\n Эмпирический параметр: %g',P0,mcp)])
xlabel('\bf Случайная величина'),
ylabel('\bf Функция плотности'),
set(gcf,'color','w')Задание 1
- Видоизмените программу так, чтобы параметры задачи вводились в одном диалоговом окне
 .
. - В соответствии с номером компьютера задайте следующие значения параметра:
№ 1:
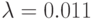 ; № 2:
; № 2: 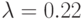 ; № 3:
; № 3: 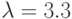 ; № 4:
; № 4: 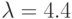 ; № 5:
; № 5: 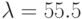 ;
;№ 6:
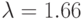 ; № 7:
; № 7: 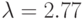 ; № 8:
; № 8: 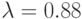 ; № 9:
; № 9: 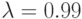 ; № 10:
; № 10: 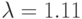 .
. - Рассчитайте оценку параметра при следующих объемах выборок (в соответствии с номером компьютера):
№ 1: n = 200; № 2: n = 300; № 3: n = 400; № 4: n = 500; № 5: n = 600; № 6: n = 700; № 7: n = 800; № 8: n = 900; № 9: n = 1000; № 10: n = 2000;
Число прогонов программы выберите по равномерному закону из следующих интервалов (в соответствии с номером компьютера):
№ 1: (10-19); № 2: (20-29); № 3: (30-39); № 4: (40-49); № 5 (50-59); № 6: (60-69); № 7: (70-79); № 8: (80-89); № 9: (90-99); № 10: (100-110).
- Проверьте, доставляет ли максимум функции правдоподобия найденная оценка параметра экспоненциального распределения?
- Напишите программу по оценке параметров нормального закона по методу максимального правдоподобия.
