НОУ ИНТУИТ | Моделирование систем. Лекция 7: Метод максимального правдоподобия точечной оценки неизвестных параметров вероятностных распределений

Учитесь и получайте официальные документы БЕСПЛАТНО. Вы можете поддержать наш проект.

Регистрация Вход

Твой путь к знаниям!

Мордовский государственный университет имени Н.П. Огарева

Опубликован: 30.11.2010 | Доступ: свободный | Студентов: 3315 / 2014 | Оценка: 4.12 / 4.13 | Длительность: 14:37:00

ISBN: 978-5-9963-0352-6

Темы: Программирование, Алгоритмы и дискретные структуры

Специальности: Программист, Системный архитектор

|

Вам нравится? Нравится 32 студентам

| Поделиться |

Поддержать курс

| Скачать электронную книгу

2. Оценка параметра биномиального распределения

Поставим задачу оценки параметра биномиального распределения методом максимального правдоподобия.

Биномиальное распределение описывает схему Бернулли испытания случайной дискретной величины в соответствии со следующей формулой (формула Бернулли):

$P_n(X=k)=C_n^kp^k(1-p)^{n-k},$

( 7.10)

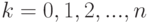где k=0,1,2,...,n , $C_n^k=\frac{n!}{k!(n-k)!}$ — биномиальные коэффициенты.

Биномиальный закон распределения (7.10) представляет собой закон распределения числа 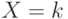X=k наступлений события (удачного испытания) в независимых испытаниях, в каждом из которых оно может произойти с одной и той же вероятностью .

Таким образом, параметром $\theta$ биномиального распределения выступает вероятность наступления события .

Характеристики биномиального распределения

Математическое ожидание:

( 7.11)

дисперсия:

( 7.12)

Величину 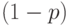(1-p) — неуспех испытания — часто обозначают через .

Ряд распределения биномиального закона приводится в таблице 7.1.

Таблица 7.1.
Распределение вероятностей биномиального закона
$x_{i}$			…		…
	$C_n^1pq^{n-1}$	$C_n^2p^2q^{n-2}$		$C_n^kp^kq^{n-k}$	...

Возможная программная реализация оценки параметра биномиального распределения методом максимального правдоподобия:

clear,clc,close all
try
  global n11
  close(n11);
end
 
try
global k11
close(k11);
end
 
try
global Nk
close(Nk)
end
 
try
    global r1
    close(r1);
end
% CВОЙСТВА ОКНА inputdlg
options.Resize = 'on';
options.WindowStyle = 'normal';
options.Interpreter = 'tex';
% ВВОД ЧИСЛА ИСПЫТАНИЙ
 N1 = inputdlg({'\bfВведите число испытаний:.......'},'Число испытаний N',1,{'13'},options);
  % ПРЕОБРАЗОВАНИЕ К ЧИСЛУ С ДВОЙНОЙ ТОЧНОСТЬЮ
N = str2num(char(N1));
if isempty(N)
    global n11
 n11 = errordlg('Число испытаний должно быть целым положительным числом','Ошибка ввода N');
return    
end
if ~isreal(N) | ~isfinite(N)
global n11
n11 = errordlg('Число испытаний должно быть целым положительным числом','Ошибка ввода N');
return
end
% КОНТРОЛЬ ВВОДА  ПАРАМЕТРА N
if prod(size(N))~=1| N < 0 | N ~= round(N)| ~isreal(N)
    n11 = errordlg('Число испытаний должно быть целым положительным числом','Ошибка ввода N');
return
end
 % ВВОД ЧИСЛА УСПЕШНЫХ ИСПЫТАНИЙ
 k1 = inputdlg({'\bfВведите число успешных испытаний:.......'},...
    'Число успешных испытаний k',1,{'9'}, options);
% ПРЕОБРАЗОВАНИЕ К ЧИСЛУ С ДВОЙНОЙ ТОЧНОСТЬЮ
k = str2num(char(k1));
 
if isempty(k)
    global n11
 n11 = errordlg('Число успешных испытаний должно быть целым положительным числом','Ошибка ввода N');
return    
end
 
if ~isreal(k) | ~isfinite(k)
global n11
n11 = errordlg('Число успешных испытаний должно быть целым положительным числом','Ошибка ввода N');
return
end
 % КОНТРОЛЬ ВВОДА ПАРАМЕТРА k
if prod(size(k)) ~= 1 | k < 0 | k ~= round(k)
    global k11
        k11 = errordlg('\bfЧисло успешных испытаний k должно быть положительным целым числом и 
  меньше общего числа испытаний N','Ошибка ввода числа k');
return
end
% КОНТРОЛЬ ВЕЛИЧИНЫ ЗНАЧЕНИЙ N и k
nums = (N-k+1) : N;
      dens = 1 : k;
      nums = nums./dens;
      c = round(prod(nums));
      if c > 1e+015
          global Nk
Nk = errordlg('\bfПроизведение N*k велико......','Ошибка');
return
      end
syms p
% ФОРМИРОВАНИЕ ФУНКЦИИ 
% МАКСИМАЛЬНОГО ПРАВДОПОДОБИЯ

% см. help nchoosek
L = nchoosek(N,k)*p^k*(1-p)^(N-k);%m^(length(t))*exp(-m*sum(t));
% ЛОГАРИФМИЧЕСКАЯ ФУНКЦИЯ МАКСИМАЛЬНОГО ПРАВДОПОДОБИЯ
Lg = log(L);
% ДИФФЕРЕНЦИРОВАНИЕ
dLg = diff(Lg,p);
% ПРЕОБРАЗОВАНИЕ СИМВОЛЬНОЙ ПЕРЕМЕННОЙ
%  К СТРОКОВОЙ 
dLg = char(dLg);
% РЕШЕНИЕ УРАВНЕНИЯ ПРАВДОПОДОБИЯ
ap1 = double(solve(dLg));
% ВЫВОД РЕЗУЛЬТАТОВ В КОМАНДНОЕ ОКНО
fprintf('\n\t БИНОМИАЛЬНОЕ РАСПРЕДЕЛЕНИЕ:\n')
fprintf('\t Число испытаний N = %d\n',N)
fprintf('\t Число успешных испытаний k = %d\n',k)
fprintf('\t Оценка параметра биномиального распределения: p = %g\n',ap1)
% РЯД РАСПРЕДЕЛЕНИЯ БИНОМИАЛЬНОГО ЗАКОНА
m = 0;
for J = 0:N
    m = m+1;
    P(m) = (factorial(N)/(factorial(J)*factorial(N-J)))*ap1^J*(1-ap1)^(N-J);
end
 
options.Resize = 'on';
options.WindowStyle = 'normal';
options.Interpreter = 'tex';
global r1
CreateStruct.WindowStyle = 'replace';
CreateStruct.Interpreter = 'tex';
r1 = msgbox('\bfРезультаты смотрите в командном окне...........','Help', CreateStruct);
 
fprintf('\t Максимальное значение вероятности успеха в N испытаниях Pmax = %g\n', max(P))
Pmax = find(P == max(P));

% УСЛОВИЕ РАСПОЛОЖЕНИЯ НАДПИСИ
if Pmax - 1 < N/2
% ДИАГРАММА РАСПРЕДЕЛЕНИЯ ВЕРОЯТНОСТЕЙ
stem(0:N,P,'filled','r'),
hold on
set(gca,'ygrid','on')
 
title('\bf Эмпирическое биномиальное распределение')
set(gcf,'color','w'),
ylim([0 1.1*max(P)])
 promt = sprintf('p = %g',ap1);
text(mean(0:N)+0.5*mean(0:N),0.95*max(P),['\bf',promt])
elseif Pmax - 1 >= N/2
stem(0:N,P,'filled','r'),

set(gca,'ygrid','on')
title('\bfЭмпирическое биномиальное распределение')

promt = sprintf('p = %g',ap1);
text(N/6,0.95*max(P),['\bf\fontsize{12}',promt])
end

xlabel('\bf Случайная величина')
ylabel('\bf Вероятность')
ylim([0 1.1*max(P)])
set(gcf,'color','w')

Задание 2

В соответствии с номером компьютера задайте следующие значения числа испытаний

и число успешных испытаний

:

№ 1: N = 10, k = 7; 
№ 2: N = 22, k = 12; 
№ 3: N = 23, k = 13; 
№ 4: N = 24, k = 14;
№ 5: N = 35, k = 25; 
№ 6: N = 36, k = 16;
№ 7: N = 37, k = 17; 
№ 8: N = 38, k = 28; 
№ 9: N = 29, k = 19;
№ 10: N = 40, k = 12.

Напишите программу оценки по методу максимального правдоподобия параметра биномиального распределения, если в 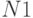независимых испытаниях событие появилось 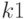раз и в 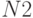независимых испытаниях событие появилось 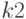раз. Число испытаний и число успешных событий принимайте в зависимости от номера компьютера:
```
№ 1: N1 = 10, k1 = 7, N2 = 11, k2 = 6;
№ 2: N1 = 12, k1 = 2, N2 = 13, k2 = 12;
№ 3: N1 = 13, k = 3, N2 = 3, k2 = 2;
№ 4: N1 = 14, k1 = 4, N2 = 10, k2 = 8;
№ 5: N1 = 15, k1 = 5, N2 = 5, k2 = 3;
№ 6: N1 = 16, k1 = 6, N2 = 16, k2 = 12;
№ 7: N1 = 17, k1 = 7, N2 = 27, k2 = 17;
№ 8: N1 = 28, k1 = 18, N2 = 18, k2 = 8;
№ 9: N1 = 29, k1 = 9, N2 = 19, k2 = 9;
№ 10: N1 = 30, k1 = 10, N2 = 20, k2 = 11.
```

3. Оценка параметра отрицательного биномиального распределения

Отрицательное биномиальное распределение носит еще название распределения Паскаля [18] и относится к дискретным распределениям. Распределение вероятностей определяется формулой

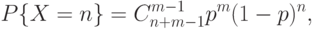$P\{X=n\}=C_{n+m-1}^{m-1}p^m(1-p)^n,$

( 7.13)

где:

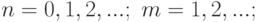
$n=0,1,2,...;\mbox{ }m=1,2,...;$

$C_{n+m-1}^{m-1}=\frac{(n+m-1)!}{(m-1)!n!}$ — биномиальные коэффициенты.

Распределение (7.13) определяет вероятность того, что потребуется провести испытаний Бернулли для появления успешных исходов.

Характеристики отрицательного биномиального распределения

Математическое ожидание:

$M[X]=\frac{m(1-p)}{p},$

( 7.14)

дисперсия:

$D[X]=\frac{m(1-p)}{p^2}.$

( 7.15)

В качестве параметра $\theta$ отрицательного биномиального распределения выступает вероятность успеха .

Ряд распределения отрицательного биномиального распределения приводится в таблице 7.2 для случая 13 испытаний и 3 успешных испытаний.

Таблица 7.2.
Распределение вероятностей отрицательного биномиального распределения

	0	1	2	...		...	13
				...	$C_{k+3-1}^{3-1}p^3(1-p)^k$	...	$105p^3(1-p)^{13}$

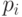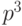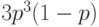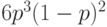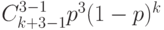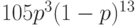Возможная программная реализация оценки параметра отрицательного биномиального распределения по методу максимального правдоподобия:

clear,clc,close all
 % CВОЙСТВА ОКНА inputdlg
options.Resize = 'on';
options.WindowStyle = 'normal';
options.Interpreter = 'tex';
% ВВОД ЧИСЛА ИСПЫТАНИЙ
 N1 = inputdlg({'\bfВвод числа испытаний:.............................................'},...
     'Число испытаний Бернулли',1,{'23'},options);
 % ПРЕОБРАЗОВАНИЕ К ЧИСЛУ С ДВОЙНОЙ ТОЧНОСТЬЮ
N = str2num(char(N1));
 
% ВВОД ЧИСЛА УСПЕШНЫХ ИСПЫТАНИЙ
options.Resize = 'on';
options.WindowStyle = 'normal';
options.Interpreter = 'tex';
 m1 = inputdlg({'\bfВвод числа успешных испытаний:................................'},...
     'Число успешных испытаний',1,{'12'},options);
% ПРЕОБРАЗОВАНИЕ К ЧИСЛУ С ДВОЙНОЙ ТОЧНОСТЬЮ
m = str2num(char(m1));
 % КОНТРОЛЬ ВЕЛИЧИНЫ ЗНАЧЕНИЙ N и k
N0 = N + m - 1;
nums = (N0 - m +1):N0;
      dens = 1:m ;
      nums = nums./dens;
      c = round(prod(nums));
      if c > 1e+015
         Nm = errordlg('Произведение N*m велико.','Ошибка');
         pause(1)
         break
      end
%--------------------------------------------------
%%% Определение символьной переменной
syms p
% ФОРМИРОВАНИЕ ФУНКЦИИ 
% МАКСИМАЛЬНОГО ПРАВДОПОДОБИЯ ПРИ N = 0
% см. help nchoosek
L0 = nchoosek(0+m-1,0)*p^m*(1-p)^0;
dL0 = diff(L0);
dL0char = char(dL0);
% РЕШЕНИЕ УРАВНЕНИЯ ПРАВДОПОДОБИЯ ПРИ N=0
x10 = solve(dL0char);
x20 = double(x10);
u = find(x20);
if length(u) == length(x20)
    x0 = 0;
elseif length(u) < length(x20)
    x20(u);
    u1 = find(x20 > 0);
    x20(u1);
    x0 = mean(x20);
end
if N > 0
% ФОРМИРОВАНИЕ ФУНКЦИИ 
% МАКСИМАЛЬНОГО ПРАВДОПОДОБИЯ ПРИ N>0
k = 0;
for I = 1:N
k = k + 1;
L = nchoosek(I + m-1,m-1)*p^m*(1-p)^I;

% ЛОГАРИФМИЧЕСКАЯ ФУНКЦИЯ
%  МАКСИМАЛЬНОГО ПРАВДОПОДОБИЯ
Lg = log(L);
% ДИФФЕРЕНЦИРОВАНИЕ
dLg = diff(Lg,p);
% ПРЕОБРАЗОВАНИЕ СИМВОЛЬНОЙ ПЕРЕМЕННОЙ
% К СТРОКОВОЙ 
dLg = char(dLg);
% РЕШЕНИЕ УРАВНЕНИЯ ПРАВДОПОДОБИЯ
ap1 = solve(dLg);
ap(k) = double(ap1);
end
app = mean([ap,x0]);
% ВЫВОД РЕЗУЛЬТАТОВ В КОМАНДНОЕ ОКНО
fprintf('\n\t ОТРИЦАТЕЛЬНОЕ БИНОМИАЛЬНОЕ РАСПРЕДЕЛЕНИЕ:\n\t %s%d\n\t %s%d\n',
  'Число испытаний Бернулли: N = ', N,'Число успешных испытаний: m = ',m)
fprintf('\n\t Оценка параметра: p = %g\n', app)
% РЯД РАСПРЕДЕЛЕНИЯ ВЕРОЯТНОСТЕЙ 
% ОТРИЦАТЕЛЬНОГО БИНОМИАЛЬНОГО ЗАКОНА
k = 0;
for J = 0:N
    k = k+1;
    P(k) = (factorial(J+m-1)/(factorial(J)*factorial(m-1)))*app^m*(1-app)^J;
end
fprintf('\t Максимальное значение вероятности при N = %d испытаниях: Pmax = %g\n', N, max(P))
n = find(P == max(P));
fprintf('\t Номер испытания с максимальной вероятностью: n = %d\n', n-1)
 r1 = helpdlg('Результаты смотрите в командном окне','Help');
 % ДИАГРАММА РАСПРЕДЕЛЕНИЯ ВЕРОЯТНОСТЕЙ
if n < N/2
h2 = figure(2);
stem(0:N,P,'filled','r'),hold on
set(gca,'ygrid','on')
text(mean(0:N)+0.5*mean(0:N),0.95*max(P),sprintf('%sp = %g','\bf',app))
elseif n >= N/2
   h2 = figure(2);
stem(0:N,P,'filled','r'),
set(gca,'ygrid','on')
text(N/20,0.95*max(P),sprintf('%sp = %g','\bf',app))
end 
end
title('\bf Эмпирическое отрицательное биномиальное распределение')
xlabel('\bf Случайная величина')
ylabel('\bf Вероятность')
ylim([0 1.1*max(P)]),

Задание 3

Для приведенной программы в соответствии с номером компьютера задайте следующие входные данные для оценки параметра (вероятности успеха) отрицательного биномиального распределения:
```
№ 1: N = 11,  m = 3;  № 2: N = 12, m = 4; № 3: N = 13, m = 5; 
№ 4: N = 14, m = 6; № 5: N = 15,  m = 16;  № 6: N = 26, m = 6; 
№ 7: N = 17, m = 17; № 8: N = 18,  m = 8; № 9: N = 19, m = 9; 
№ 10: N = 20,  m = 10.
```
Постройте график изменения максимальной вероятности отрицательного биномиального распределения в зависимости от числа успешных испытаний ( ) при заданном числе испытаний ( ) в соответствии с номером компьютера (см. п. 1). Диапазон изменения числа успешных испытаний принимайте от 1 до 10.
Проверьте диаграмму распределения вероятностей отрицательного биномиального распределения с помощью функции с выбором для заданного числа испытаний и произведенной оценки параметра.
Постройте график распределения вероятностей отрицательного биномиального распределения на основе функции .

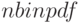Контрольные вопросы

Что называется точечной оценкой параметров?
В каких случаях применяется отрицательное биноминальное распределение?
Что называется логарифмической функцией правдоподобия?
Что называется уравнением правдоподобия?
Что называется состоятельной оценкой параметра вероятностного распределения?
В каких случаях оценка параметра вероятностного распределения будет несмещенной?

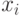
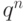
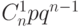
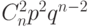
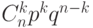
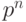
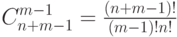Дальше >>

Авторизоваться

Моделирование систем

Метод максимального правдоподобия точечной оценки неизвестных параметров вероятностных распределений

2. Оценка параметра биномиального распределения

Характеристики биномиального распределения

3. Оценка параметра отрицательного биномиального распределения

Характеристики отрицательного биномиального распределения

Контрольные вопросы

Вопросы и ответы