НОУ ИНТУИТ | Математика криптографии и теория шифрования. Лекция 10: Усовершенствованный стандарт шифрования (AES

Учитесь и получайте официальные документы БЕСПЛАТНО. Вы можете поддержать наш проект.

Регистрация Вход

Твой путь к знаниям!

Опубликован: 19.01.2010 | Доступ: свободный | Студентов: 3545 / 610 | Оценка: 4.28 / 4.00 | Длительность: 26:16:00

ISBN: 978-5-9963-0242-0

Темы: Безопасность, Математика

Специальности: Математик

|

Вам нравится? Нравится 71 студенту

| Поделиться |

Поддержать курс

| Скачать электронную книгу

Алгоритм

Алгоритм 10.1 — простой алгоритм для процедуры расширения ключа (версия AES-128).

10.1. Программа на псевдокоде для расширения ключей в AES128

Пример 10.1

Таблица 10.3 показывает, как вычисляются ключи для каждого раунда. Предполагается, что между Алисой и Бобом согласован ключ шифра на 128 битов — (24 75 A2 B3 34 75 56 88 31 E2 12 00 13 AA 54 87) ₁₆.

Таблица 10.3. Пример расширения ключей
Раунд	Значения t	Первое слово в раунде	Второе слово в раунде	Третье слово в раунде	Четвертое слово в раунде
-		w₀₀=2475A2B3	w₀₁=34755688	w₀₂=31E21200	w₀₃=13AA5487
1	AD20177D	w₀₄=8955B5CE	w₀₅=BD20E346	w₀₆=8CC2F146	w₀₇=9F68A5C1
2	470678DB	w₀₈=CE53CD15	w₀₉=73732E53	w₁₀=FFB1DF15	w₁₁=60D97AD4
3	31DA48DO	w₁₂=FF8985C5	w₁₃=8CFAAB96	w₁₄=734B7483	w₁₅=2475A2B3
4	47AB5B7D	w₁₆=B822DEB8	w₁₇=34D8752E	w₁₈=479301AD	w₁₉=54010FFA
5	6C762D20	w₂₀=D454F398	w₂₁=E08C86B6	w₂₂=A71F871B	w₂₃=F31E88E1
6	52C4F80D	w₂₄=86900B95	w₂₅=661C8D23	w₂₆=C1030A38	w₂₇=321D82D9
7	E4133523	w₂₈=62833EB6	w₂₉=049FB395	w₃₀=C59CB9AD	w₃₁=F7813B74
8	8CE29268	w₃₂=EE61ACDE	w₃₃=EAFE1F4B	w₃₄=2F62A6E6	w₃₅=D8E39D92
9	OA5E4F61	w₃₆=E43FE3BF	w₃₇=OEC1FCF4	w₃₈=21A35A12	w₃₉=F940C780
10	3PC6CD99	w₄₀=DBF92E26	w₄₁=D538D2D2	w₄₂=F49B88CO	w₄₃=ODDB4F40

В каждом раунде вычисление последних трех слов очень просто. Для вычисления первого слова мы должны сначала вычислить значение временного слова (t). Например, первое t (для раунда 1 ) вычислено как

$RotWord (13AA5487) = AA548713 \to SubWord (AA548713) = AC20177D \\ t = AC20177D \oplus Rcon_{1} = AC20 17 7D \oplus 01000000_{16} = AD20177D$

Пример 10.2

Каждый ключ раунда в AES зависит от предыдущих ключей раунда. Зависимость, однако, нелинейная из-за преобразования SubWord. Сложение констант раунда также гарантирует, что каждый ключ раунда будет отличаться от предыдущего.

Пример 10.3

Два множества ключей раунда могут быть созданы от двух шифроключей, которые различаются только в одном бите.

Как показывает таблица 10.4, имеются существенные разности между двумя соответствующими ключами раунда — R означает "раунд", B и D означают разность битов.

Таблица 10.4. Сравнение двух множеств ключей раунда
R.	Ключи для множества 1				Ключи для множества 2				B.D.
-	1245A2A1	2331A4A3	B2CCAA34	C2BB7723	1245A2A1	2331A4A3	B2CCAB34	C2BB7723	01
1	F9B08484	DA812027	684D8A13	AAF6FD30	F9B08484	DA812027	684D8B13	AAF6FC30	02
2	B9E48028	6365AOOF	OB282A1C	A1DED72C	B9008028	6381AOOF	OBCC2B1C	A13AD72C	17
3	AOEAF11A	C38F5115	C8A77B09	6979AC25	3DOEF11A	5E8F5115	55437A09	F479AD25	30
4	1E7BCEE3	DDF49FF6	1553E4FF	7C2A48DA	839BCEA5	DD149FBO	8857E5B9	7C2E489C	31
5	EB2999F3	36DD0605	238EE2FA	5FA4AA20	A2C910B5	7FDD8F05	F78A6ABC	8BA42220	34
6	82852E3C	B4582839	97D6CAC3	C87260E3	CB5AA788	B487288D	430D4231	C8A96011	56
7	82553FD4	360D17ED	A1DBDD2E	69A9BDCD	588A2560	ECODODED	AF004FDC	67A92FCD	50
8	D12F822D	E72295CO	46F948EE	2F50F523	OB9F98E5	E7929508	4892DAD4	2F3BF519	44
9	99C9A438	7EEB31F8	38127916	17428C35	F2794CFO	15EBD9F8	5D79032C	7242F635	51
10	83AD32C8	FD460330	C5547A26	D216F613	E83BDABO	FDD00348	AOA90064	D2EBF651	52

Пример 10.4

Понятие слабых ключей, которое мы обсуждали для DES в "Стандарт шифрования данных (DES)" , не применимо к AES. Предположим, что все биты в ключе шифра — нули. Ниже для этого случая показаны слова для некоторых раундов:

Все слова перед раундом и в первом раунде равны между собой. Во втором раунде первое слово соответствует третьему; второе слово соответствует четвертому. Однако после второго раунда совпадений нет; каждое слово различно.

Расширение ключа в AES-192 и AES-256

Алгоритмы расширения ключей в AES-192 и AES-256 — очень похожи на алгоритм расширения ключа в AES-128, со следующими отличиями:

1. В AES-192 слова сгенерированы в группы по шесть вместо четырех.

a. Ключ шифра создает первые шесть слов ( w₀ к w₅ ).

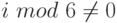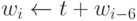b. Если $i\ mod\ 6 \ne 0$ , то ${w_i} \leftarrow {w_{i - 1}} + {w_{i - 6}}$ ; иначе ${w_i} \leftarrow t + {w_{i - 6}}$ .

1. В AES-256 слова сгенерированы в группы по восемь вместо четырех.

a. Ключ шифра создает первые восемь слов ( w₀ до w₇ ).

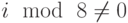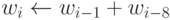b. Если $i{\text{ }}\bmod {\text{ }}8 \ne 0$ , то ${w_i} \leftarrow {w_{i - 1}} + {w_{i - 8}}$ ; иначе, w_i <-t + w_i-8.

c. Если i mod 4=0, но 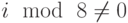$i{\text{ }}\bmod {\text{ }}8 \ne 0$ , то w_i = Subword (w_i-1) + w_i-8.

Анализ расширения ключа

Механизм расширения ключа в AES был разработан так, чтобы обеспечить несколько свойств, которые срывают действия криптоаналитика по раскрытию сообщения.

Даже если Ева знает только часть ключа шифра или значения слов в некотором ключевом раунде, этого недостаточно: она еще должна найти остальную часть ключа шифра, прежде чем сможет найти ключи всех раундов. Это обеспечивается нелинейностью процесса расширения ключа, полученной с помощью преобразования SubWord.
Два различных ключа шифра, независимо от того, как они соотносятся друг с другом, производят два расширения, которые отличаются по крайней мере в нескольких раундах.
Каждый бит ключа шифра изменяется в нескольких раундов. Например, изменение единственного бита в ключе шифра изменяет некоторые биты в нескольких раундах.
Использование констант, RCons, удаляет любую симметрию, которая может быть создана другими преобразованиями.
В отличие от DES в AES отсутствуют любые слабые ключи.
Процесс расширения ключа может быть легко реализован на всех платформах.
Процедура расширения ключа может быть реализована без применения отдельных таблиц; вычисления могут быть сделаны с использованием полей GF(2⁸) и FG(2).

Дальше >>

Математика криптографии и теория шифрования