|
Прошел экстерном экзамен по курсу перепордготовки "Информационная безопасность". Хочу получить диплом, но не вижу где оплатить? Ну и соответственно , как с получением бумажного документа? |
Модульная арифметика
Расширенный алгоритм Евклида
Даны два целых числа a и b. Нам зачастую надо найти другие два целых числа, s и t, такие, которые
s x a + t x b = НОД(a,b)
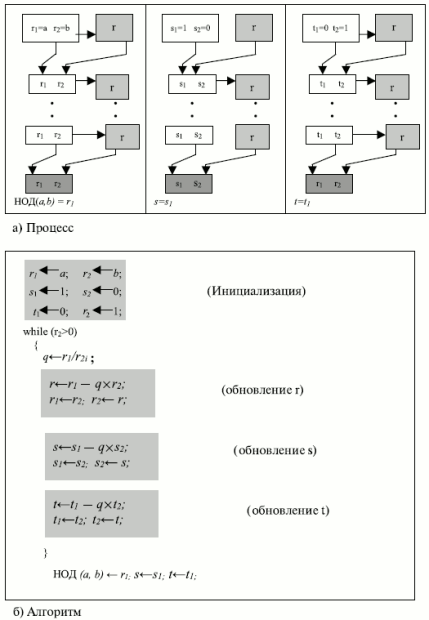
Расширенный алгоритм Евклида может вычислить НОД (a, b) и в то же самое время вычислить значения s и t. Алгоритм и процесс такого вычисления показан на рис. 2.8.
Здесь расширенный алгоритм Евклида использует те же самые шаги, что и простой алгоритм Евклида. Однако в каждом шаге мы применяем три группы вычислений вместо одной. Алгоритм использует три набора переменных: r, s и t.
На каждом шаге переменные r1, r2 и r используются так же, как в алгоритме Евклида. Переменным r1 и r2 присваиваются начальные значения a и b соответственно. Переменным s1 и s2 присваиваются начальные значения 1 и 0 соответственно. Переменным t1 и t2 присваиваются начальные значения 0 и 1, соответственно. Вычисления r, s и t одинаковы, но с одним отличием. Хотя r — остаток от деления r1 на r2, такого соответствия в других двух группах вычислений нет. Есть только одно частное, q, которое вычисляется как r1/r2 и используется для других двух вычислений.
Пример 2.9
Дано a = 161 и b = 28, надо найти НОД (a, b) и значения s и t.
Решение
r = r1 – q x r2 s = s1 – qs2 t = t1 – q x t2
Для отображения алгоритма мы используем следующую таблицу:
| q | r1 | r2 | R | s1 | s2 | s | t1 | t2 | t |
|---|---|---|---|---|---|---|---|---|---|
| 5 | 161 | 28 | 21 | 1 | 0 | 1 | 0 | 1 | -5 |
| 1 | 28 | 21 | 7 | 0 | 1 | -1 | 1 | -5 | 6 |
| 3 | 21 | 7 | 0 | 1 | -1 | 4 | -5 | 6 | -23 |
| 7 | 0 | -1 | 4 | 6 | -23 |
Мы получаем НОД (161, 28) = 7, s = –1 и t = 6. Ответы могут быть проверены, как это показано ниже.
(–1) x 161 + 6 x 28 = 7
Пример 2.10
Дано a = 17 и b = 0, найти НОД (a, b) и значения s и t.
Решение
Для отображения алгоритма мы используем таблицу.
Обратите внимание, что нам не надо вычислять q, r и s. Первое значение r2 соответствует условию завершения алгоритма. Мы получаем НОД (17, 0) = 17, s = 1 и t = 0. Это показывает, почему мы должны придавать начальные значения s1 — 1 и t1 — 0. Ответы могут быть проверены так, как это показано ниже:
(1 x 17) + (0 x 0) = 17
Пример 2.11
Даны a = 0 и b = 45, найти НОД (a, b) и значения s и t.
Решение
Для отображения алгоритма мы используем следующую таблицу:
Мы получаем НОД (0,45) = 45, s = 0 и t = 1. Отсюда ясно, что мы должны инициализировать s2 равным 0, а t2 — равным 1. Ответ может быть проверен, как это показано ниже:
(0 x 0) + (1 x 45) = 45
Линейные диофантовы уравнения
Хотя очень важное приложение расширенного алгоритма Евклида будет рассмотрено далее, здесь мы остановимся на другом приложении — "нахождение решения линейных диофантовых уравнений двух переменных", а именно, уравнения ax + by = c. Мы должны найти значения целых чисел для x и y, которые удовлетворяют этому уравнению. Этот тип уравнения либо не имеет решений, либо имеет бесконечное число решений. Пусть d = НОД (a, b). Если d†c, то уравнение не имеет решения. Если d|c, то мы имеем бесконечное число решений. Одно из них называется частным, остальные — общими.
Частное решение
Если d|c, то можно найти частное решение вышеупомянутого уравнения, используя следующие шаги.
- Преобразуем уравнение к a1x + b1y = c1, разделив обе части уравнения на d. Это возможно, потому, что d делит a, b, и c в соответствии с предположением.
- Найти s и t в равенстве a1s + b1t = 1, используя расширенный алгоритм Евклида.
- Частное решение может быть найдено:
Общие решения
После нахождения частного решения общие решения могут быть найдены:
Пример 2.12
Найти частные и общие решения уравнения 21x + 14y = 35.
Решение
Мы имеем d = НОД (21, 14) = 7. При 7|35 уравнение имеет бесконечное число решений. Мы можем разделить обе стороны уравнения на 7 и получим уравнение 3x + 2y = 5. Используя расширенный алгоритм Евклида, мы находим s и t, такие, что 3s + 2t = 1. Мы имеем S = 1 и t = –1. Решения будут следующие:
Частное решение : x0 = 5 x 1=5 и y0 = 5 x (–1) = -5 тогда 35/7 =5 Общие: x = 5+ k x 2 y= –5 – k x 3 где k — целое
Поэтому решения будут следующие (5, –5), (7, –8), (9, –11)...
Мы можем легко проверить, что каждое из этих решений удовлетворяет первоначальному уравнению.
Пример 2.13
Рассмотрим очень интересное приложение решения диофантовых уравнений в реальной жизни. Мы хотим найти различные комбинации объектов, имеющих различные значения. Например, мы хотим обменять денежный чек 100$ на некоторое число банкнот 20$ и несколько банкнот по 5$. Имеется много вариантов, которые мы можем найти, решая соответствующее диофантово уравнение 20x + 5y = 100. Обозначим d = НОД (20, 5) = 5 и 5|100. Уравнение имеет бесконечное число решений, но в этом случае приемлемы только несколько из них (только те ответы, в которых и x и y являются неотрицательными целыми числами). Мы делим обе части уравнения на 5, чтобы получить 4x + y = 20, и решаем уравнение 4s + t = 1. Мы можем найти s = 0 и t = 1, используя расширенный алгоритм Эвклида. Частное решение:  и
и 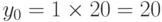 .
Общие решения с неотрицательными x и y — (0, 20), (1, 16), (2, 12), (3, 8), (4, 4), (5, 0). Остальная часть решений неприемлема, потому что y становится отрицательным. Кассир в банке должен спросить, какую из вышеупомянутых комбинаций мы хотим. Первое число в скобках обозначает число банкнот по 20$ ; второе число обозначает число банкнот по 5$.
.
Общие решения с неотрицательными x и y — (0, 20), (1, 16), (2, 12), (3, 8), (4, 4), (5, 0). Остальная часть решений неприемлема, потому что y становится отрицательным. Кассир в банке должен спросить, какую из вышеупомянутых комбинаций мы хотим. Первое число в скобках обозначает число банкнот по 20$ ; второе число обозначает число банкнот по 5$.