|
Не могу найти требования по оформлению выпускной контрольной работы по курсу профессиональной переподготовки "Менеджмент предприятия" |
Описание неопределенностей в теории принятия решений
Одна из основных проблем в теории принятия решений - необходимость учета неопределенностей, оценки и управления рисками. Для описания неопределенностей и рисков применяют различные подходы.
Чаще всего используется вероятностно-статистический подход. Kратко обсуждаются основные понятия и результаты в области теории вероятностей и статистики.
Изложение в настоящей главе доведено до современного уровня. Одним из наиболее интересных и продуктивных бурно развивающихся направлений теории принятия решений является анализ интервальных данных, согласно которому исходные данные - не числа, а интервалы. Таким образом, неопределенность величин, используемых в процессе принятия решения, моделируется путем замены конкретных численных значений на интервалы, в которых содержатся рассматриваемые величины.
Интервальные данные - это частный случай нечетких данных. В последнее время теория нечеткости все чаще используется в экономических исследованиях. Нечеткость, расплывчатость, размытость понятий и величин - типичная черта многих задач принятия решений.Обратим внимание на систему принципиально важных утверждений, согласно которой теория нечеткости в определенном смысле сводится к теории случайных множеств - одной из частей вероятностно-статистической теории.
Настоящая глава содержит введение в методы описания неопределенностей. За более подробной информацией необходимо обратиться к специальной литературе.
Вероятностно-статистические методы описания неопределенностей
Статистика - это наука о том, как обрабатывать данные. Статистические методы основаны на вероятностных моделях. Они активно применяются в технических исследованиях, экономике, теории и практике управления (менеджмента). А также в социологии, медицине, геологии, истории и т.д. С обработкой результатов наблюдений, измерений, испытаний, опытов, анализов имеют дело специалисты во всех отраслях практической деятельности, почти во всех областях научных исследований.
Развитие наукоемких технологий, как правило, основано на применении высоких статистических технологий организации и управления производством. Особенно активно они используются в высокотехнологичных отраслях промышленности. Без вероятностно-статистических методов немыслимы оценка и анализ риска, страхование, финансовая деятельность. Инженеры, менеджеры, экономисты, социологи, врачи, психологи, историки успешно применяют интеллектуальные инструменты принятия решений, основанные на вероятности и статистике.
Статистические методы и модели и их база - теория вероятностей - активно развиваются во всем мире. Американская статистическая ассоциация насчитывает более двадцати тысяч членов, Королевское статистическое общество - более десяти тысяч. Статьи по вероятности и статистике постоянно публикуются более чем в пятистах научных журналах. В университетах США статистических факультетов больше, чем математических и физических. Восемь нобелевских премий получены эконометриками (специалистами по статистическим методам в экономике).
Современная теория вероятностей основана на аксиоматике академика АН СССР А.Н. Колмогорова. Однако в нашей стране специалисты и научные работники, студенты и преподаватели пока еще недостаточно знакомы с последними достижениями в области вероятностно-статистических методов, хотя ссылки на них постоянно встречаются в научно-технической, деловой и учебной литературе.
Вероятность и статистика нужны всем. Теория вероятностей и математическая статистика - основа вероятностно-статистических методов обработки данных. А данные мы обрабатываем и анализируем прежде всего для принятия решений. Чтобы воспользоваться современным математическим аппаратом, необходимо рассматриваемые задачи выразить в терминах вероятностно-статистических моделей.
Применение конкретного вероятностно-статистического метода состоит из трех этапов:
- переход от экономической, управленческой, технологической реальности к абстрактной математико-статистической схеме, т.е. построение вероятностной модели системы управления, технологического процесса, процедуры принятия решений, в частности по результатам статистического контроля, и т.п.
- проведение расчетов и получение выводов чисто математическими средствами в рамках вероятностной модели;
- интерпретация математико-статистических выводов применительно к реальной ситуации и принятие соответствующего решения (например, о соответствии или несоответствии качества продукции установленным требованиям, необходимости наладки технологического процесса и т.п.), в частности, заключения (о доле дефектных единиц продукции в партии, о конкретном виде законов распределения контролируемых параметров технологического процесса и др.).
Математическая статистика использует понятия, методы и результаты теории вероятностей. Далее рассматриваем основные вопросы построения вероятностных моделей в экономических, управленческих, технологических и иных ситуациях. Подчеркнем, что для активного и правильного использования нормативно-технических и инструктивно-методических документов (инструкций, методик, правил, стандартов, справочников, учебников и т.п.) по вероятностно-статистическим методам нужны предварительные знания. Так, необходимо знать, при каких условиях следует применять тот или иной документ, какую исходную информацию необходимо иметь для его выбора и применения, какие решения должны быть приняты по результатам обработки данных и т.д.
Примеры применения теории вероятностей и математической статистики.Рассмотрим несколько примеров, когда вероятностно-статистические модели являются хорошим инструментом для решения управленческих, производственных, экономических, народнохозяйственных задач. Так, например, в романе А.Н.Толстого "Хождение по мукам" (т.1) говорится: "Мастерская дает двадцать три процента брака, этой цифры вы и держитесь, - сказал Струков Ивану Ильичу".
Как понимать эти слова в разговоре заводских менеджеров? Одна единица продукции не может быть дефектна на 23%. Она может быть либо годной, либо дефектной. Наверно, Струков имел в виду, что в партии большого объема содержится примерно 23% дефектных единиц продукции. Тогда возникает вопрос, а что значит "примерно"? Пусть из 100 проверенных единиц продукции 30 окажутся дефектными, или из 1000 - 300, или из 100000 - 30000 и т.д., надо ли обвинять Струкова во лжи?
Или другой пример. Монетка, которую используют как жребий, должна быть "симметричной". При ее бросании в среднем в половине случаев должен выпадать герб (орел), а в половине случаев - решетка (решка, цифра). Но что означает "в среднем"? Если провести много серий по 10 бросаний в каждой серии, то часто будут встречаться серии, в которых монетка 4 раза выпадает гербом. Для симметричной монеты это будет происходить в 20,5% серий. А если на 100000 бросаний окажется 40000 гербов, то можно ли считать монету симметричной? Процедура принятия решений строится на основе теории вероятностей и математической статистики.
Пример может показаться недостаточно серьезным. Однако это не так. Жеребьевка широко используется при организации промышленных технико-экономических экспериментов. Например, при обработке результатов измерения показателя качества (момента трения) подшипников в зависимости от различных технологических факторов (влияния консервационной среды, методов подготовки подшипников перед измерением, влияния нагрузки подшипников в процессе измерения и т.п.). Допустим, необходимо сравнить качество подшипников в зависимости от результатов хранения их в разных консервационных маслах, т.е. в маслах состава А и В. При планировании такого эксперимента возникает вопрос, какие подшипники следует поместить в масло состава А, а какие - в масло состава В, но так, чтобы избежать субъективизма и обеспечить объективность принимаемого решения. Ответ на этот вопрос может быть получен с помощью жребия.
Аналогичный пример можно привести и с контролем качества любой продукции. Чтобы решить, соответствует или не соответствует контролируемая партия продукции установленным требованиям, из нее отбирается выборка. По результатам контроля выборки делается заключение о всей партии. В этом случае очень важно избежать субъективизма при формировании выборки, т.е. необходимо, чтобы каждая единица продукции в контролируемой партии имела одинаковую вероятность быть отобранной в выборку. В производственных условиях отбор единиц продукции в выборку обычно осуществляют не с помощью жребия, а по специальным таблицам случайных чисел или с помощью компьютерных датчиков случайных чисел.
Похожие проблемы обеспечения объективности сравнения возникают при сопоставлении различных схем организации производства, оплаты труда, при проведении тендеров и конкурсов, подбора кандидатов на вакантные должности и т.п. Всюду нужна жеребьевка или подобные ей процедуры.
Пусть надо выявить наиболее сильную и вторую по силе команду при организации турнира по олимпийской системе (проигравший выбывает). Допустим, что более сильная команда всегда побеждает более слабую. Ясно, что самая сильная команда однозначно станет чемпионом. Вторая по силе команда выйдет в финал тогда и только тогда, когда до финала у нее не будет игр с будущим чемпионом. Если такая игра запланирована, то вторая по силе команда в финал не попадет. Тот, кто планирует турнир, может либо досрочно "выбить" вторую по силе команду из турнира, сведя ее в первой же встрече с лидером, либо обеспечить ей второе место, обеспечив встречи с более слабыми командами вплоть до финала. Чтобы избежать субъективизма, проводят жеребьевку. Для турнира из 8 команд вероятность того, что в финале встретятся две самые сильные команды, равна 4/7. Соответственно с вероятностью 3/7 вторая по силе команда покинет турнир досрочно.
При любом измерении единиц продукции (с помощью штангенциркуля, микрометра, амперметра и т.п.) имеются погрешности. Чтобы выяснить, есть ли систематические погрешности, необходимо сделать многократные измерения единицы продукции, характеристики которой известны (например, стандартного образца). При этом следует помнить, что кроме систематической погрешности присутствует и случайная погрешность.
Поэтому встает вопрос, как по результатам измерений узнать, есть ли систематическая погрешность. Если отмечать только, является ли полученная при очередном измерении погрешность положительной или отрицательной, то эту задачу можно свести к уже рассмотренной. Действительно, сопоставим измерение с бросанием монеты, положительную погрешность - с выпадением герба, отрицательную - решетки (нулевая погрешность при достаточном числе делений шкалы практически никогда не встречается). Тогда проверка отсутствия систематической погрешности эквивалентна проверке симметричности монеты.
Итак, задача проверки отсутствия систематической погрешности сведена к задаче проверки симметричности монеты. Проведенные рассуждения приводят к так называемому "критерию знаков" в математической статистике.
При статистическом регулировании технологических процессов на основе методов математической статистики разрабатываются правила и планы статистического контроля процессов, направленные на своевременное обнаружение разладки технологических процессов и принятия мер к их наладке и предотвращению выпуска продукции, не соответствующей установленным требованиям. Эти меры нацелены на сокращение издержек производства и потерь от поставки некачественных единиц продукции. При статистическом приемочном контроле на основе методов математической статистики разрабатываются планы контроля качества путем анализа выборок из партий продукции. Сложность заключается в том, чтобы уметь правильно строить вероятностно-статистические модели принятия решений. В математической статистике для этого разработаны вероятностные модели и методы проверки гипотез, в частности, гипотез о том, что доля дефектных единиц продукции равна определенному числу р0, например,  (вспомните слова Струкова из романа А.Н.Толстого).
(вспомните слова Струкова из романа А.Н.Толстого).
Задачи оценивания. В ряде управленческих, производственных, экономических, народнохозяйственных ситуаций возникают задачи другого типа - задачи оценки характеристик и параметров распределений вероятностей.
Рассмотрим пример. Пусть на контроль поступила партия из  электроламп. Из этой партии случайным образом отобрана выборка объемом n электроламп. Возникает ряд естественных вопросов. Как по результатам испытаний элементов выборки определить средний срок службы электроламп, с какой точностью можно оценить эту характеристику? Как изменится точность, если взять выборку большего объема? При каком числе часов Т можно гарантировать, что не менее 90% электроламп прослужат Т и более часов?
электроламп. Из этой партии случайным образом отобрана выборка объемом n электроламп. Возникает ряд естественных вопросов. Как по результатам испытаний элементов выборки определить средний срок службы электроламп, с какой точностью можно оценить эту характеристику? Как изменится точность, если взять выборку большего объема? При каком числе часов Т можно гарантировать, что не менее 90% электроламп прослужат Т и более часов?
Предположим, что при испытании выборки объемом n электроламп дефектными оказались Х электроламп. Какие границы можно указать для числа D дефектных электроламп в партии, для уровня дефектности 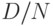 и т.п.?
и т.п.?
Или при статистическом анализе точности и стабильности технологических процессов надлежит оценить такие показатели качества, как среднее значение контролируемого параметра и степень его разброса в рассматриваемом процессе. Согласно теории вероятностей в качестве среднего значения случайной величины целесообразно использовать ее математическое ожидание, а в качестве статистической характеристики разброса - дисперсию, среднее квадратическое отклонение или коэффициент вариации. Возникают вопросы: как оценить эти статистические характеристики по выборочным данным, с какой точностью это удается сделать?
Аналогичных примеров можно привести очень много. Здесь важно было показать, как теория вероятностей и математическая статистика могут быть использованы в инженерных, экономических и управленческих задачах.
Современное представление о математической статистике. Под математической статистикой понимают "раздел математики, посвященный математическим методам сбора, систематизации, обработки и интерпретации статистических данных, а также использованию их для научных или практических выводов. Правила и процедуры математической статистики опираются на теорию вероятностей, позволяющую оценить точность и надежность выводов, получаемых в каждой задаче на основании имеющегося статистического материала". При этом статистическими данными называются сведения о числе объектов в какой-либо более или менее обширной совокупности, обладающих теми или иными признаками.
По типу решаемых задач математическая статистика обычно делится на три раздела: описание данных, оценивание и проверка гипотез.
По виду обрабатываемых статистических данных математическая статистика делится на четыре направления:
- одномерная статистика (статистика случайных величин), в которой результат наблюдения описывается действительным числом;
- многомерный статистический анализ, где результат наблюдения над объектом описывается несколькими числами (вектором);
- статистика случайных процессов и временных рядов, где результат наблюдения - функция;
- статистика объектов нечисловой природы, в которой результат наблюдения имеет нечисловую природу, например, является множеством (геометрической фигурой), упорядочением или получен в результате измерения по качественному признаку.
Исторически первой появились некоторые области статистики объектов нечисловой природы (в частности, задачи оценивания доли брака и проверки гипотез о ней; первоначально говорилось об извлечении разноцветных шаров из урны) и одномерная статистика. Математический аппарат для них проще, поэтому на их примере обычно демонстрируют основные идеи математической статистики.
Лишь те методы обработки данных, т.е. математической статистики, являются доказательными, которые опираются на вероятностные модели соответствующих реальных явлений и процессов. Речь идет о моделях поведения потребителей, возникновения рисков, функционирования технологического оборудования, получения результатов эксперимента, течения заболевания и т.п. Вероятностную модель реального явления следует считать построенной, если рассматриваемые величины и связи между ними выражены в терминах теории вероятностей. Соответствие вероятностной модели реальности, т.е. ее адекватность, обосновывают, в частности, с помощью статистических методов проверки гипотез.
Невероятностные методы обработки данных являются поисковыми, их можно использовать лишь при предварительном анализе данных, так как они не дают возможности оценить точность и надежность выводов, полученных на основании ограниченного статистического материала.
Вероятностные и статистические методы применимы всюду, где удается построить и обосновать вероятностную модель явления или процесса. Их применение обязательно, когда сделанные на основе выборочных данных выводы переносятся на всю совокупность (например, с выборки на всю партию продукции).
В конкретных областях применений используются как вероятностно-статистические методы широкого применения, так и специфические. Например, в разделе производственного менеджмента, посвященного статистическим методам управления качеством продукции, используют прикладную математическую статистику (включая планирование экспериментов). С помощью ее методов проводится статистический анализ точности и стабильности технологических процессов и статистическая оценка качества. К специфическим методам относятся методы статистического приемочного контроля качества продукции, статистического регулирования технологических процессов, оценки и контроля надежности и др.
Широко применяются такие прикладные вероятностно-статистические дисциплины, как теория надежности и теория массового обслуживания. Содержание первой из них ясно из названия, вторая занимается изучением систем типа телефонной станции, на которую в случайные моменты времени поступают вызовы - требования абонентов, набирающих номера на своих телефонных аппаратах. Длительность обслуживания этих требований, т.е. длительность разговоров, также моделируется случайными величинами. Большой вклад в развитие этих дисциплин внесли член-корреспондент АН СССР А.Я. Хинчин (1894-1959), академик АН УССР Б.В.Гнеденко (1912-1995) и другие отечественные ученые.
Коротко об истории математической статистики. Математическая статистика как наука начинается с работ знаменитого немецкого математика Карла Фридриха Гаусса (1777-1855), который на основе теории вероятностей исследовал и обосновал метод наименьших квадратов, созданный им в 1795 г. и примененный для обработки астрономических данных (с целью уточнения орбиты малой планеты Церера). Его именем часто называют одно из наиболее популярных распределений вероятностей - нормальное, а в теории случайных процессов основной объект изучения - гауссовские процессы.
В конце XIX в. - начале ХХ в. крупный вклад в математическую статистику внесли английские исследователи, прежде всего К.Пирсон (1857-1936) и Р.А.Фишер (1890-1962). В частности, Пирсон разработал критерий "хи-квадрат" проверки статистических гипотез, а Фишер - дисперсионный анализ, теорию планирования эксперимента, метод максимального правдоподобия оценки параметров.
В 30-е годы ХХ в. поляк Ежи Нейман (1894-1977) и англичанин Э.Пирсон развили общую теорию проверки статистических гипотез, а советские математики академик А.Н. Колмогоров (1903-1987) и член-корреспондент АН СССР Н.В.Смирнов (1900-1966) заложили основы непараметрической статистики. В сороковые годы ХХ в. румын А. Вальд (1902-1950) построил теорию последовательного статистического анализа.
Математическая статистика бурно развивается и в настоящее время. Так, за последние 40 лет можно выделить четыре принципиально новых направления исследований:
- разработка и внедрение математических методов планирования экспериментов;
- развитие статистики объектов нечисловой природы как самостоятельного направления в прикладной математической статистике;
- развитие статистических методов, устойчивых по отношению к малым отклонениям от используемой вероятностной модели;
- широкое развертывание работ по созданию компьютерных пакетов программ, предназначенных для проведения статистического анализа данных.
Вероятностно-статистические методы и оптимизация. Идея оптимизации пронизывает современную прикладную математическую статистику и иные статистические методы. А именно, методы планирования экспериментов, статистического приемочного контроля, статистического регулирования технологических процессов и др. С другой стороны, оптимизационные постановки в теории принятия решений, например, прикладная теория оптимизации качества продукции и требований стандартов, предусматривают широкое использование вероятностно-статистических методов, прежде всего прикладной математической статистики.
В производственном менеджменте, в частности, при оптимизации качества продукции и требований стандартов особенно важно применять статистические методы на начальном этапе жизненного цикла продукции, т.е. на этапе научно-исследовательской подготовки опытно-конструкторских разработок (разработка перспективных требований к продукции, аванпроекта, технического задания на опытно-конструкторскую разработку). Это объясняется ограниченностью информации, доступной на начальном этапе жизненного цикла продукции, и необходимостью прогнозирования технических возможностей и экономической ситуации на будущее. Статистические методы должны применяться на всех этапах решения задачи оптимизации - при шкалировании переменных, разработке математических моделей функционирования изделий и систем, проведении технических и экономических экспериментов и т.д.
В задачах оптимизации, в том числе оптимизации качества продукции и требований стандартов, используют все области статистики. А именно, статистику случайных величин, многомерный статистический анализ, статистику случайных процессов и временных рядов, статистику объектов нечисловой природы. Разработаны рекомендации по выбору статистического метода для анализа конкретных данных .
