|
Не могу найти требования по оформлению выпускной контрольной работы по курсу профессиональной переподготовки "Менеджмент предприятия" |
Организационно-экономическая система управления материальными запасами промышленных корпоративных систем
Определение оптимальной стратегии нестационарной детерминированной системы управления запасами методом динамического программирования.Опишем решение поставленной задачи методом динамического программирования в соответствии со схемой, приведенной выше.
Рассмотрим последовательно определение оптимального управления на шаге 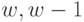 и т. д., используя принцип оптимальности Р. Беллмана.
и т. д., используя принцип оптимальности Р. Беллмана.
Рассмотрим  -ый шаг:
-ый шаг:
 - состояние системы к началу
- состояние системы к началу  -го шага (
-го шага (  );
);
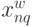 - управление на
- управление на  -м шаге;
-м шаге;
Следует отметить, что если шаги 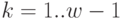 могут заканчиваться какой-либо поставкой, то шаг
могут заканчиваться какой-либо поставкой, то шаг  представляет собой только расходование запаса до уровня
представляет собой только расходование запаса до уровня  без последующей поставки в момент времени
без последующей поставки в момент времени  , т. е.
, т. е. 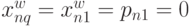 . Динамика изменения величины запаса
. Динамика изменения величины запаса  в течение периода планирования
в течение периода планирования  представлена на рис. 4.14.
представлена на рис. 4.14.
Множество возможных состояний на  -м шаге
-м шаге 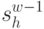 можно получить из уравнений состояний (4.28):
можно получить из уравнений состояний (4.28):
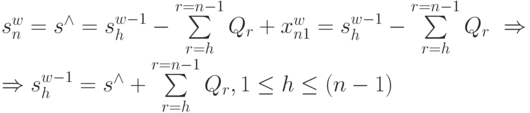 |
( n-1) |
Целевую функцию (величину затрат на хранение и поддержание запаса) в течение  -го шага получаем из (4.32):
-го шага получаем из (4.32):
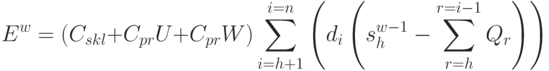 |
( 4.34) |
Поскольку  , то
, то  не зависит от
не зависит от 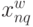 , следовательно условный минимум целевой функции на
, следовательно условный минимум целевой функции на  -м шаге:
-м шаге:
 |
( 4.35) |
Рассчитав  для всех возможных
для всех возможных 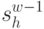 , получим функцию оптимальных затрат на
, получим функцию оптимальных затрат на  -м шаге при условии действия управления
-м шаге при условии действия управления  .
.
Рассмотрим шаг  . Множество возможных состояний
. Множество возможных состояний 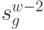 получаем из уравнений состояний (4.28):
получаем из уравнений состояний (4.28):
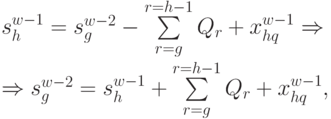 |
( 4.36) |
где  ,
,  ,
, 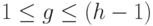 ,
, 
Для любых возможных состояний 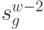 и возможных управлений
и возможных управлений  из (6.23) получаем:
из (6.23) получаем:
 |
( 4.37) |
С учетом уравнения состояния (4.36) 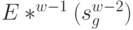 зависит только от
зависит только от  и
и  . В результате минимизации только по одной переменной
. В результате минимизации только по одной переменной  согласно уравнению (4.37) получим две функции:
согласно уравнению (4.37) получим две функции:  и
и 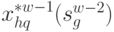 .
.
Далее рассматривается трехшаговая задача: к двум последним шагам присоединяется 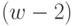 -й и т. д.
-й и т. д.
Рассмотрим общий случай определения оптимального управления на шаге  (
( 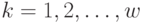 ). Множество возможных состояний
). Множество возможных состояний 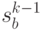 в начале шага
в начале шага  определяется из (4.28):
определяется из (4.28):
 |
( 4.38) |
Минимум целевой функции на  шагах при условии, что перед
шагах при условии, что перед  -м шагом система находилась в состоянии
-м шагом система находилась в состоянии 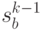 , определяется как:
, определяется как:
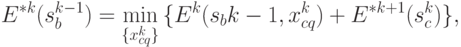 |
( 4.39) |
где
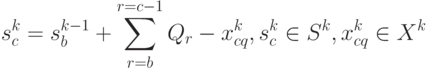 |
( 4.40) |
Таким образом, определив из (4.35) значения  для всех допустимых
для всех допустимых 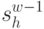 при условии действия управления
при условии действия управления  , а из (4.39) и уравнений состояний (4.40) значения
, а из (4.39) и уравнений состояний (4.40) значения 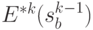 и соответствующие
и соответствующие 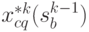 , получим последовательности:
, получим последовательности:
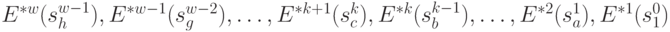 -
-
условные минимумы целевой функции на последнем, на двух последних, на 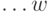 последних шагах и
последних шагах и
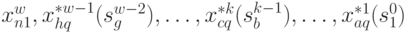 -
-
условные оптимальные управления на  -м,
-м,  -м,
-м, 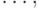
 -м шагах.
-м шагах.
Используя эти последовательности, находим решение задачи. При фиксированном  получаем
получаем  .
.
Если  представляет собой множество, т. е.
представляет собой множество, т. е.  , то
, то  , где состояние
, где состояние 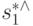 , такое, что:
, такое, что:

Далее из (4.40) определяем  и т. д.:
и т. д.:
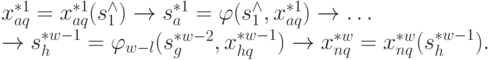
Таким образом, получаем оптимальную стратегию:

где 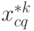 определяет величину
определяет величину 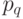 и момент времени
и момент времени  поставки
поставки  в оптимальной стратегии управления запасами
в оптимальной стратегии управления запасами  для поставленной задачи.
для поставленной задачи.
Поставленная задача имеет ряд ограничений на размер поставки, на величину текущего запаса, на минимальный интервал времени между соседними поставками.
Ограничения на размер поставки учтены в уравнении для допустимых величин поставки (4.25).
Ограничения на величину текущего запаса, минимальный интервал времени между поставками учитываются при определении множеств допустимых состояний 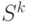 на каждом шаге
на каждом шаге 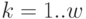 .
.
Расчетное множество состояний на шаге  определяется из (4.38) на основе множества допустимых состояний
определяется из (4.38) на основе множества допустимых состояний 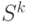 на шаге
на шаге  и множества допустимых управлений
и множества допустимых управлений 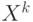 на шаге
на шаге  . Каждое состояние на шаге
. Каждое состояние на шаге 
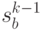 характеризуется моментом времени
характеризуется моментом времени  и расчетным уровнем запаса
и расчетным уровнем запаса  в этот момент времени.
в этот момент времени.
Учет ограничений на величину запаса проводится путем отсеивания тех расчетных состояний 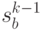 , при которых уровень запаса
, при которых уровень запаса  не соответствует указанным ограничениям.
не соответствует указанным ограничениям.
Учет ограничения на минимальный интервал времени между соседними поставками проводится путем отсеивания тех расчетных состояний 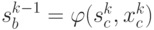 , для которых
, для которых  .
.
Таким образом, множество допустимых состояний на шаге  с учетом всех ограничений можно описать следующим образом:
с учетом всех ограничений можно описать следующим образом:

Определение множества допустимых состояний осуществляется на каждом шаге 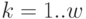 .
.
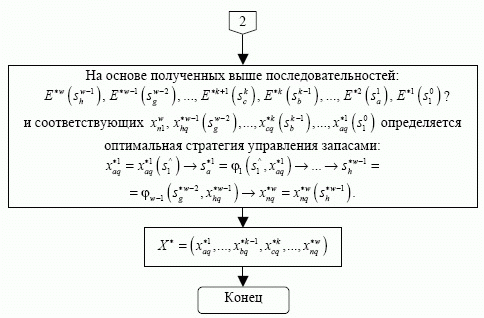
На рис. 4.15 представлена блок-схема алгоритма решения задачи нахождения оптимальной стратегии управления запасами для нестационарной детерминированной системы.

 - конечное
- конечное