НОУ ИНТУИТ | Теория экономических механизмов. Лекция 6: Теоремы Эрроу и Гиббарда-Саттертуэйта

Учитесь и получайте официальные документы БЕСПЛАТНО. Вы можете поддержать наш проект.

Регистрация Вход

Твой путь к знаниям!

Опубликован: 05.08.2011 | Доступ: свободный | Студентов: 1544 / 82 | Оценка: 4.50 / 3.50 | Длительность: 18:52:00

ISBN: 978-5-9963-0014-3

Темы: Математика, Экономика

Специальности: Математик, Экономист

|

Вам нравится? Нравится 44 студентам

| Поделиться |

Поддержать курс

| Скачать электронную книгу

Теорема Эрроу

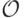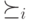В этом параграфе мы перейдем к чуть более общей формулировке и докажем, что все равно ничего не получается. Как и прежде, через $\mathcal O$ мы будем обозначать множество возможных исходов. На этом множестве у каждого из агентов есть некоторый профиль предпочтений, который мы будем обозначать через $\succeq_i$ : для двух исходов и будем писать, что $x\succeq_i y$ , если агент предпочитает исход перед .

Определение 6.1. Профиль предпочтений $\succeq$ называется рациональным, если он является линейным порядком, то есть любые два исхода сравнимы и выполняется условие транзитивности: для всяких $x,y,z\in\mathcal O$ , если $x\succeq y$ и $y \succeq z$ , то $x\succeq z$ .

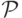Мы будем предполагать, что профили предпочтений бывают всякие. Например, всякие рациональные — их множество мы обозначим через $\mathcal R$ . Или вообще всякие профили, лишь бы любые два исхода были различимы: множество таких исходов мы обозначим через $\mathcal P$ . Если агентов , то, значит, множество всевозможных предпочтений будет в этих обозначениях $\mathcal R^N$ или $\mathcal P^N$ .

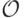Функция социального выбора в данном контексте — это некоторая функция с областью определения $\mathcal R^N$ или $\mathcal P^N$ и областью значений $\mathcal O$ , которая по данным предпочтениям агентов выбирает исход. Мы чуть обобщим это определение и будем считать, что функция социального выбора выдает не один исход, а слабый линейный порядок на имеющихся исходах (то есть $f:\mathcal R^N\to \mathbb R$ ); этот порядок мы будем обозначать через $\succeq_{f(\succeq_1,\ldots,\succeq_N)}$ или, когда ясно, на каком входе берется функция, просто $\succeq_f$ .

Мы бы хотели, чтобы функция социального выбора удовлетворяла тем естественным условиям, которые мы сформулировали в 6.1. Сначала — принцип единогласия, он же эффективность по Парето.

Определение 6.2. Пусть пара исходов $x,y\in\mathcal O$ такова, что для каждого агента исход не хуже, и при этом для какого-нибудь агента он строго лучше: для всех $x\succeq_i y$ , и существует такое , что $x\succ_j y$ . Тогда функция социального выбора называется эффективной по Парето, если для каждой такой пары исходов результат функции социального выбора $f(\succeq_1,\ldots,\succeq_N)$ ставит перед : $x\succeq_f y$ .

Затем сформулируем формально свойство попарной независимости предпочтений: результат функции должен зависеть только от относительных предпочтений сравниваемых исходов, а не от каких-то третьих возможностей.

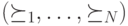Определение 6.3. Функция социального выбора удовлетворяет свойству попарной независимости предпочтений, если для каждой пары профилей $(\succeq_1,\ldots,\succeq_N)$ и $(\succeq^\prime_1,\ldots,\succeq^\prime_N)$ , если для каждого $x \succeq_i y$ тогда и только тогда, когда $x\succeq^\prime_i y$ :

$\forall i\quad x \succeq_i y \Leftrightarrow x\succeq^\prime_i y,$

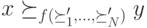то в результате $x \succeq_{f(\succeq_1,\ldots,\succeq_N)} y$ тогда и только тогда, когда $x\succeq_{f(\succeq^\prime_1,\ldots,\succeq^\prime_N)} y$ :

$\forall i\quad x \succeq_{f(\succeq_1,\ldots,\succeq_N)} y \Leftrightarrow x\succeq_{f(\succeq^\prime_1,\ldots,\succeq^\prime_N)} y.$

Наконец, последнее определение будет касаться уже не того, чего бы нам хотелось, а того, что у нас в итоге получится.

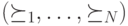
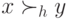Определение 6.4. Функция социального выбора называется диктаторской, если существует такой агент , что для любых $x,y\in\mathcal O$ и любого профиля $(\succeq_1,\ldots,\succeq_N)$ $x\succeq_f y$ тогда и только тогда, когда $x\succ_h y$ .

Проще говоря, диктаторская функция социального выбора делает точно такой же выбор, как один из представленных агентов. Конечно, у диктаторской функции получится соответствовать нужным свойствам, точно так же как у предпочтений одного агента это получается (проверьте это формально!). А беда в том, что ничего другого-то и не получится. Мы наконец готовы к тому, чтобы сформулировать и доказать теорему Эрроу [3].

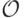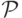Теорема 6.1. (Эрроу) Пусть множество возможных исходов $\mathcal O$ состоит из не менее чем трех элементов, и возможны все рациональные профили ( $\mathcal R$ ) или все профили, в которых любые две альтернативы различимы ( $\mathcal P$ ). Тогда всякая функция социального выбора , которая оптимальна по Парето и удовлетворяет условию попарной независимости, является диктаторской.

Доказательство.

Начнем доказательство с определения, простите за тавтологию, определяющих наборов агентов — ключевого понятия для этого доказательства теоремы Эрроу.

Определение 6.5. Для данного будем говорить, что набор агентов $S\subset [N]$ (через [N] мы обозначим множество индексов от до ):

определяющий для перед , если когда каждый агент в предпочитает $x\succ y$ и каждый агент в $[N]\setminus S$ предпочитает $y\succ x$ , выбирает ;
определяющий, если он определяющий для любой пары $\{x,y\}$ ;
полностью определяющий, если когда каждый агент из предпочитает $x\succ y$ , тоже предпочитает $x\succ_f y$ .

Важное замечание: первое из этих определений достаточно слабое, оно касается только ситуаций, когда агенты из голосуют за , а все агенты не из голосуют за ; но из него мы быстро перейдем и к более сильным ситуациям.

Доказательство мы проведем в... десять этапов. Не будем, пожалуй, оформлять каждый из этих этапов в отдельную лемму, а просто последовательно их приведем. В каждом пункте ниже выделенное курсивом утверждение — то, что хочется доказать, а в следующем абзаце идет его доказательство. Большинство доказательств однотипны: мы пользуемся тем, что множество возможных предпочтений достаточно богато, и строим такой профиль предпочтений, из которого будет следовать нужный результат.

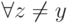Если для некоторых и набор $S\subset [N]$ является определяющим для перед , то $\forall z\neq x$ набор является определяющим для перед и $\forall z\neq y$ набор является определяющим для перед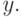
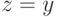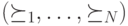Если , доказывать нечего. Если $z\neq y$ , то рассмотрим такой профиль $(\succeq_1,\ldots,\succeq_N)$ , что

$\begin{array}{rl} x\succ_i y\succ_i z & \forall i\in S,\\ y\succ_i z\succ_i x & \forall i\in [N]\setminus S.\end{array}$

Тогда, значит, по свойству определяющего набора должна предпочесть перед . А по оптимальности по Парето предпочитает перед . Значит, предпочитает перед . Осталось сослаться на попарную независимость.
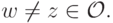
Если для некоторых и набор $S\subset [N]$ является определяющим для перед , и — третья альтернатива, то набор является определяющим для перед и для перед для всех $w\neq z\in\mathcal O.$
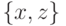По шагу 1, определяющий для перед и для перед . Применим снова шаг 1 для пары $\{x,z\}$ и альтернативы ; из шага 1 видно, что будет определяющим и для перед . Аналогичное рассуждение проходит и для пары $\{z,y\}$ .
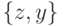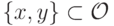
Если для некоторых $\{x,y\}\subset\mathcal O$ определяющий для перед , то определяющий.
Доказательство сразу следует из шага 2 и из того, что третья альтернатива существует (здесь это важно!).
Если определяющий и определяющий, то $S\cap T$ тоже определяющий.
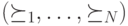Рассмотрим тройку альтернатив $\{x,y,z\}\subset\mathcal O$ и такой профиль $(\succeq_1,\ldots,\succeq_N)$ , что

$\begin{array}{ll} z \succ_i y \succ_i x \quad &\forall i\in S\setminus(S\cap T), \\ x \succ_i z \succ_i y \quad &\forall i\in S\cap T, \\ y \succ_i x \succ_i z \quad &\forall i\in T\setminus(S\cap T), \\ y \succ_i z \succ_i x \quad &\forall i\in [N]\setminus(S\cup T). \end{array}$

Тогда $z\succ_f y$ , потому что $S=(S\cap T)\cup(S\setminus(S\cap T))$ — определяющий, и $x\succ_f z$ , потому что — определяющий. Значит, $x\succ_f y$ , и по попарной независимости $S\cap T$ тоже является определяющим для перед . Значит, он и вообще определяющий.
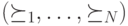Для любого $S\subset [N]$ либо определяющий, либо его дополнение $[N]\setminus S$ определяющий. Рассмотрим тройку альтернатив $x,y,z\in\mathcal O$ и такой профиль предпочтений $(\succeq_1,\ldots,\succeq_N)$ , что
$\begin{array}{ll} x \succ_i z \succ_i y &\forall i\in S, \\ y \succ_i x \succ_i z &\forall i\in [N]\setminus S. \end{array}$

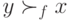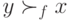Тогда либо $x\succ_f y$ , и определяющий для перед , либо $y\succ_f x$ . Если $y\succ_f x$ , то по свойству оптимальности по Парето $x\succ_f z$ , и, значит, $y\succ_f z$ ; значит, $[N]\setminus S$ является определяющим набором для перед

.
Если определяющий и $S\subset T$ , то определяющий.
Пустой набор не может быть определяющим из-за свойства оптимальности по Парето. Значит, $[N]\setminus T$ не может быть определяющим, потому что тогда и $\emptyset = S\cap ([N]\setminus T)$ будет определяющим. Значит, по пункту 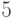, определяющий.
Если $S\subset [N]$ определяющий, и , то есть строгое подмножество $S^\prime\subsetneq S$ , тоже являющееся определяющим набором.
Рассмотрим 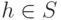$h\in S$ . Если $S\setminus\{h\}$ определяющий, то утверждение доказано. Если нет, то $[N]\setminus(S\setminus\{h\})$ определяющий, и

$\{h\} = S\cap ([N]\setminus(S\setminus\{h\}))$

определяющий.
Для некоторого $h\in [N]$ $\{h\}$ определяющий.
Нужно просто несколько раз применить шаг 7.
Если $S\subset [N]$ определяющий, то для всех и полностью определяющий для перед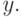
Нужно получить, что для всех $T\subset [N]\setminus S$ $x\succ_f y$ , если все агенты из предпочитают $x\succ y$ , все агенты из предпочитают $x\succeq y$ , а остальные — $y\succ x$ .

Рассмотрим третью альтернативу и такой профиль 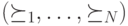$(\succeq_1,\ldots,\succeq_N)$ , что

$\begin{align*} x & \succ_i z \succ_i y \quad &\forall i\in S, \\ x & \succ_i y \succ_i z \quad &\forall i\in T, \\ y & \succ_i z \succ_i x \quad &\forall i\in [N]\setminus (S\cup T). \end{align*}$

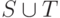Тогда $x\succ_f z$ , потому что $S\cup T$ определяющий, и $z\succ_f y$ , потому что определяющий. Значит, $x\succ_f y$ , что и требовалось.
Если $\{h\}$ определяющий, то — диктатор.
Это в точности следует из определения полностью определяющего набора.

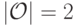Как видите, мы неоднократно и по делу пользовались тем, что $|\mathcal O|\ge 3$ . В самом деле, если $|\mathcal O|=2$ , то теорема неверна: функция социального выбора "большинство голосов", как мы уже отмечали в предыдущем параграфе, и недиктаторская, и оптимальная по Парето, и обладает свойством попарной независимости предпочтений.

Дальше >>

Авторизоваться

Теория экономических механизмов

Теоремы Эрроу и Гиббарда-Саттертуэйта

Теорема Эрроу

Вопросы и ответы