Теорема об эквивалентности доходности
Введение
Итак, в аукционе участвуют 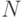 покупателей (агентов). У каждого из них есть своя внутренняя ценность
покупателей (агентов). У каждого из них есть своя внутренняя ценность 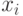 , которая определяется случайной величиной
, которая определяется случайной величиной 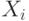 , распределенной по одному и тому же распределению
, распределенной по одному и тому же распределению 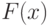 (в этой лекции мы будем находиться в симметричном случае). Первый момент множества из
(в этой лекции мы будем находиться в симметричном случае). Первый момент множества из 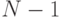 агентов, то есть случайную величину, характеризующую максимальную цену из них, обозначим через
агентов, то есть случайную величину, характеризующую максимальную цену из них, обозначим через 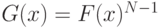 . Мы ограничимся стандартными аукционами, в которых вещь достается тому, кто больше всех предложил. При этом, конечно, то, сколько он в действительности заплатит, зависит от формы аукциона.
. Мы ограничимся стандартными аукционами, в которых вещь достается тому, кто больше всех предложил. При этом, конечно, то, сколько он в действительности заплатит, зависит от формы аукциона.
Для аукциона 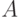 и агента
и агента 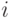 введем обозначение
введем обозначение 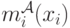 — сколько участник
— сколько участник 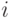 ожидает заплатить, участвуя в
ожидает заплатить, участвуя в 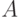 и используя равновесную стратегию (предполагается, что равновесие в
и используя равновесную стратегию (предполагается, что равновесие в 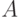 существует). Агенты в симметричном случае одинаковые, поэтому
существует). Агенты в симметричном случае одинаковые, поэтому  не зависит от
не зависит от 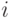 . Введем вдобавок начальное условие: участник со ставкой
. Введем вдобавок начальное условие: участник со ставкой  платит
платит  .
.
Кроме того, мы будем предполагать, что агенты нейтральны к риску (risk-neutral). Нейтральный к риску агент не делает разницы между распределениями своего дохода с разными дисперсиями. Проще говоря, для него заплатить 10$, чтобы с вероятностью  получить 20$, — честная сделка с нулевым доходом. В случае, когда агенты осторожны (risk-averse) и надежный доход предпочитают случайным величинам, анализ всех этих ситуаций достаточно существенно меняется; мы сейчас не будем рассматривать эту ситуацию.
получить 20$, — честная сделка с нулевым доходом. В случае, когда агенты осторожны (risk-averse) и надежный доход предпочитают случайным величинам, анализ всех этих ситуаций достаточно существенно меняется; мы сейчас не будем рассматривать эту ситуацию.
Теорема будет достаточно удивительной: окажется, что в любом равновесии ожидаемые выплаты агентов (а значит, и доход продавца) одинаковы! То есть можно не ожидать, что при помощи какой-нибудь хитрой схемы аукционер сможет максимизировать свой доход, — при эгоистичных агентах, которые могут успешно рассчитать оптимальную стратегию, доходы будут совершенно однаковыми. Впервые похожий эффект заметил основатель всей теории аукционов Викри [76,77]. А теорему независимо доказали Майерсон [55] и Райли и Самуэльсон [69].
Теорема эквивалентности доходности
Начнем с формулировки теоремы эквивалентности доходности, которая касается введенных выше обозначений. Мы будем устанавливать эквивалентность доходности в терминах "дохода продавца" Revenue, но доказывать будем для ожидаемых выплат каждого из агентов. Если агент 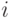 участвует в аукционе
участвует в аукционе 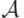 , его ожидаемая выплата равна
, его ожидаемая выплата равна
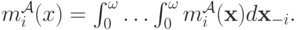
А ожидание дохода продавца получается как сумма всех ожидаемых выплат покупателей:
![\mathbf E[\mathrm{Revenue}] = \mathbf E\left[\sum\limits_{i=1}^N m^{\mathcal A}_i(x)\right] = N\mathbf E\left[m^{\mathcal A}(x)\right],](/sites/default/files/tex_cache/a21d316eb7f33c1c91c50d7e82371810.png)
если мы находимся в симметричном случае, где все агенты равноправны.
Теорема 4.1. Пусть скрытые значения агентов 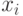 распределены независимо и одинаково, и все агенты нейтральны к риску. Тогда любое симметричное равновесие любого стандартного аукциона, такое, что ожидаемая выплата агента со ставкой 0 равна нулю, дает один и тот же ожидаемый доход продавцу.
распределены независимо и одинаково, и все агенты нейтральны к риску. Тогда любое симметричное равновесие любого стандартного аукциона, такое, что ожидаемая выплата агента со ставкой 0 равна нулю, дает один и тот же ожидаемый доход продавцу.
Доказательство. Будем следовать схеме, которую мы уже излагали в доказательстве теоремы 3.2. Рассмотрим первого агента: остальные следуют равновесной стратегии  , а он ставит некоторое значение
, а он ставит некоторое значение 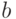 . Поскольку
. Поскольку 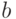 — тоже возможная ставка, существует некоторое
— тоже возможная ставка, существует некоторое 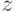 , для которого
, для которого 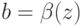 . Здесь
. Здесь 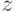 можно рассматривать как "ложную" внутреннюю стоимость: можно считать, что агент делает ставку по стратегии
можно рассматривать как "ложную" внутреннюю стоимость: можно считать, что агент делает ставку по стратегии  , но просто подменяет свою истинную внутреннюю стоимость
, но просто подменяет свою истинную внутреннюю стоимость 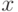 на
на 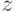 .
.
Агент выигрывает, когда его ставка 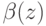 превышает самую большую из других ставок
превышает самую большую из других ставок  , то есть (так как
, то есть (так как  возрастает) когда
возрастает) когда 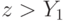 . Тогда игрок ожидает получить следующую прибыль:
. Тогда игрок ожидает получить следующую прибыль:
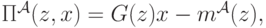
где 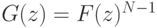 (распределение
(распределение 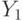 ). Заметим, что
). Заметим, что 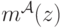 зависит от
зависит от  и от
и от 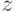 , но не зависит от внутренней ценности
, но не зависит от внутренней ценности 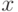 .
.
Нам нужно максимизировать прибыль, которую агент ожидает получить. Метод максимизации будет самый что ни на есть классический: взять производную и приравнять ее нулю. Дифференцируя выражение для ожидаемой прибыли по 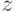 , получим следующее равенство:
, получим следующее равенство:
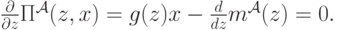
Но мы находимся в равновесии, а это значит, что агенту нужно поступать в соответствии со стратегией  , применяя ее к своей истинной скрытой ценности. Иначе говоря, максимум достигается, если агент берет
, применяя ее к своей истинной скрытой ценности. Иначе говоря, максимум достигается, если агент берет 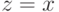 и сообщает
и сообщает 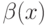 . Приравняв в предыдущем уравнении
. Приравняв в предыдущем уравнении 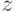 и
и 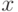 , получим следующее:
, получим следующее:
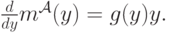
Когда мы найдем решение этого дифференциального уравнения, мы получим выражение для 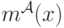 :
:
![m^{\mathcal A}(x) = m^{\mathcal A}(0) + \int_0^xyg(y)dy = \int_0^xyg(y)dy = G(x)\times \mathbf E[Y_1|Y_1<x].](/sites/default/files/tex_cache/67ea5c9080922101159ff4a546857f88.png)
В итоге у нас получилось, что ожидаемая выплата агента не зависит от 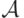 , а только от распределения на
, а только от распределения на 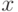 . Поскольку ожидаемый доход продавца складывается из ожидаемых выплат агентов, получается, что этот доход тоже не зависит от
. Поскольку ожидаемый доход продавца складывается из ожидаемых выплат агентов, получается, что этот доход тоже не зависит от 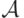 .
.
Давайте рассмотрим на простом примере, как можно подсчитать ожидаемые выплаты агентов и ожидаемую прибыль продавца.
Пример 4.1.
Пусть скрытые значения агентов 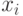 распределены равномерно на
распределены равномерно на ![[0,1]](/sites/default/files/tex_cache/ccfcd347d0bf65dc77afe01a3306a96b.png) . Тогда
. Тогда  ,
,  , и из теоремы получается, что
, и из теоремы получается, что
![m^{\mathcal A}(x) &=& \frac{N-1}Nx^{N}, \\
\mathbf E[m^{\mathcal A}(x)] &=& \frac{N-1}{N(N+1)}.](/sites/default/files/tex_cache/b4c9673ee71f5e5139e51dfdbf77a2e8.png)
А ожидаемый доход продавца — это ![N\cdot\mathbf E[m^{\mathcal A}(x)]](/sites/default/files/tex_cache/2876ae22df1223fb0fcbe201a7ef12f1.png) :
:
![\mathbf E[R^{\mathcal A}] = \frac{N-1}{N+1}.](/sites/default/files/tex_cache/3befe02ad512c994ba0c503c8089b3d7.png)
Конец примера 4.1.
Математики говорят: "Theorems come and go, a good formula stays for ever" ("Теоремы приходят и уходят, хорошая формула остается навсегда"). Во время доказательства теоремы мы получили формулу для ожидаемой выплаты агента. Эта формула,
![m^{\mathcal A}(x) = m^{\mathcal A}(0) + \int_0^xyg(y)dy = G(x)\cdot \mathbf E[Y_1|Y_1<x],](/sites/default/files/tex_cache/4237cd3948842b5e3f21ed0f41864651.png)
в будущем пригодится нам, разумеется, гораздо чаще, чем сама формулировка теоремы. Заметим, что формула действует только если равновесие в аукционе есть — это нужно проверять отдельно, а уже потом, если получилось, что равновесие есть, использовать эту формулу.
Два нестандартных аукциона
В качестве примеров применения теоремы эквивалентности доходности (точнее, волшебной формулы из предыдущего параграфа) рассмотрим два аукциона, которые окажутся весьма интересными и с математической, и с экономической точки зрения.
Пример 4.2. Рассмотрим аукцион, в котором платят все (по-английски такая ситуация называется all-pay auction). Здесь все агенты делают ставки, потом все платят, сколько поставили, а вещь при этом дают тому, кто заплатил больше. В таком аукционе ожидаемая выплата строго равна ставке. Поэтому если равновесие есть, оно должно быть таким:
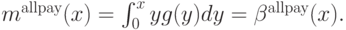
Проверим, что это действительно равновесие (хотя бы по Нэшу). Пусть все играют по  , а один агент ставит
, а один агент ставит  . Тогда он получит
. Тогда он получит

Это мы уже видели в лекции "Принцип выявления предпочтений" , когда рассматривали аукцион первой цены. Здесь тоже применим совершенно тот же вывод, и, следовательно, здесь тоже будет достигнуто равновесие.
Конец примера 4.2.
Наверное, читатели удивляются: кто ж согласится участвовать в таком невыгодном аукционе? Однако пример есть, и недалеко от поверхности. Этот аукцион представляет собой модель лоббирования: каждая из группировок, которые хотят добиться нужного результата в парламенте, платят за лоббирование, но результат-то один! Чуть менее чистый пример — рекламные кампании: все тратят деньги, а лидирующее положение на рынке занимает одна компания (это, правда, не всегда так).
Второй пример — аукцион, при анализе которого нам потребуется немного вспомнить математическую статистику.
Пример 4.3. В аукционе третьей цены все похоже на аукционы первой и второй цены — агенты делают ставки, побеждает тот, кто поставил больше всех, но победитель платит только третью сверху ставку, а не вторую и не первую. Здесь будет много интересного из статистики, а в конце получится довольно забавный результат.
Итак, наша магическая формула подсказывает:
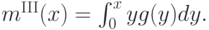
Игрок выигрывает, когда 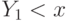 , и платит третью сверху цену. С учетом того, что равновесная стратегия
, и платит третью сверху цену. С учетом того, что равновесная стратегия 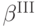 является неубывающей функцией, выплата выигравшего игрока будет равна
является неубывающей функцией, выплата выигравшего игрока будет равна 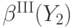 , где
, где 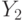 — вторая сверху внутренняя ценность из оставшегося
— вторая сверху внутренняя ценность из оставшегося 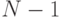 игрока.
игрока.
Теперь на время забудем об аукционах и займемся статистикой. Найдем плотность второй порядковой статистики в выборке из 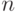 элементов.
элементов.
Событие  — это объединение двух непересекающихся событий:
— это объединение двух непересекающихся событий:
- все
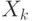 меньше
меньше 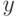 ;
; -
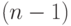 величина из
величина из 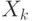 меньше
меньше 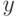 , но один какой-то
, но один какой-то 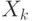 больше
больше 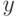 .
.
Следовательно, для функции распределения этой случайной величины мы получим следующее выражение:
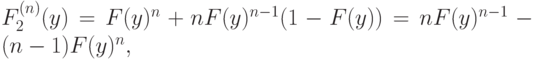
и, продифференцировав, получим плотность
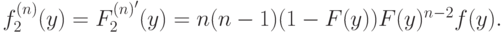
Нас еще интересуют условные вероятности. Сначала — совместная вероятность; поскольку мы предполагаем, что все 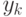 независимы, ее плотность просто равна произведению плотностей:
независимы, ее плотность просто равна произведению плотностей:

Теперь построим формулу для 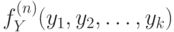 :
:
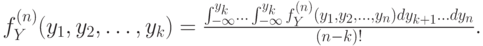
Пределы интегрирования в этом выражении описывают тот факт, что переменные с 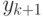 до
до  должны оказаться меньше
должны оказаться меньше 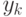 . А в знаменателе стоит
. А в знаменателе стоит 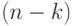 !, потому что при подсчете интегралов мы посчитаем одни и те же события
!, потому что при подсчете интегралов мы посчитаем одни и те же события 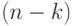 ! раз (это получается из-за того, что формула совместной вероятности не различает значения переменных
! раз (это получается из-за того, что формула совместной вероятности не различает значения переменных  , по которым идет интегрирование, друг относительно друга).
, по которым идет интегрирование, друг относительно друга).
Теперь подставим формулу для совместной вероятности (с 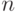 переменными) и проинтегрируем получившееся выражение. Интегрировать в данном случае — дело совсем нехитрое:
переменными) и проинтегрируем получившееся выражение. Интегрировать в данном случае — дело совсем нехитрое:
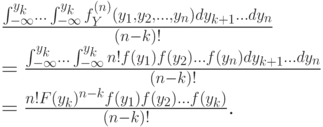
Например, при  мы получим следующее выражение:
мы получим следующее выражение:
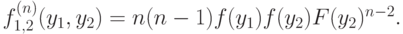
Теперь можно вывести формулу и для условной вероятности:
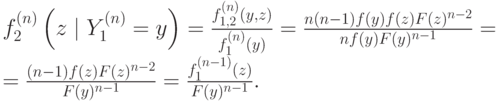
Найдем условную вероятность второй порядковой статистики при условии первой; для этого выпишем определение условной вероятности, а затем упростим полученное выражение:
![f_2^{(n)}\left(y\mid Y_1^{(n)} < x\right) = \frac{\int^x_{y}f_{1,2}^{(n)}(z,y)dz}{F_{1}^{(n)}(x)} = \\ = \frac{1}{F_{1}^{(n)}(x)}\int^x_{y}n(n-1)f(z)f(y)F(y)^{n-2}dz = \\ = \frac{1}{F_{1}^{(n)}(x)}\left[n(n-1)F(z)f(y)F(y)^{n-2}\right]^y_x = \frac{n(F(x)-F(y))f_1^{(n-1)}(y)}{F_1^{(n)}(x)}.](/sites/default/files/tex_cache/038a455d5fa7d116c98c5f7aa4310a58.png)
Получив таким образом условную вероятность второй порядковой статистики, можно уже подсчитать и ожидаемую выплату:
![m^{\mathrm{III}}(x) = F_1^{(N-1)}(x)\mathbf E\left[\beta^{\mathrm{III}}(Y_2)\mid Y_1<x\right] = \\ = \int_0^x\beta^{\mathrm{III}}(y)(N-1)(F(x)-F(y))f_1^{(N-2)}(y)dy.](/sites/default/files/tex_cache/ac037bc72bc0f495f78c3829226b996f.png)
Приравняем это выражение к тому, что дает нам полученная при доказательстве теоремы 4.1 формула:
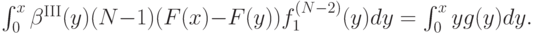
Продифференцировав по  , получим:
, получим:
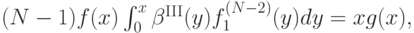
то есть
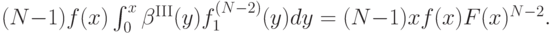
Так как  , получается, что
, получается, что
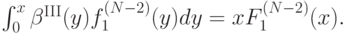
Теперь продифференцируем это равенство по  :
:
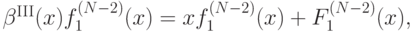
а затем выразим отсюда 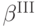 :
:
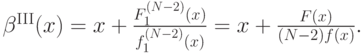
Итак, мы получили итоговую формулу оптимальной стратегии:
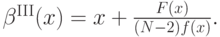
К сожалению, это все верно, только когда  возрастает; а для этого, как видно из этой же формулы, надо, чтобы
возрастает; а для этого, как видно из этой же формулы, надо, чтобы 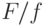 возрастало. Иначе говоря (вспомним, что
возрастало. Иначе говоря (вспомним, что  — это производная
— это производная 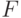 , то есть
, то есть 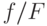 — это производная
— это производная 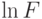 ),
), 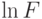 должен быть вогнутой функцией (в такой ситуации говорят, что
должен быть вогнутой функцией (в такой ситуации говорят, что 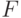 log-вогнута, log-concave).
log-вогнута, log-concave).
А обещанный интересный эффект вот в чем. У нас получилось, что 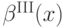 всегда строго больше
всегда строго больше 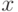 , а это значит, что агенту всегда оптимально ставить строго больше, чем свое истинное значение скрытой ценности. Несколько неожиданно, но в общем вполне логично: можно ожидать, что уж третий-то сверху окажется ниже истинной стоимости.
, а это значит, что агенту всегда оптимально ставить строго больше, чем свое истинное значение скрытой ценности. Несколько неожиданно, но в общем вполне логично: можно ожидать, что уж третий-то сверху окажется ниже истинной стоимости.
Конец примера 4.3.
