Классы данных в Mathematica
2.3. Списки
Последним классом данных, которого мы ещё не коснулись, являются списки.
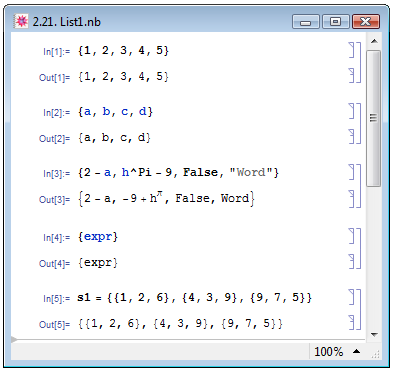
Список представляет собой удобную форму структурирования данных, по строению представляет собой множество элементов, заключённых в фигурные скобки { } и разделённых запятыми: {expr1,expr2,...}. Все списки относятся к сложным выражениям.
В качестве элементов списка expr1, expr2,... могут выступать как однотипные (примеры In[1] и In[2] на рис. 2.21), так и разнотипные (пример In[3]) данные. Список может содержать и один элемент: тогда он выглядит как некоторое выражение, обособленное скобками (пример In[4]). Элементы списка сами могут являться списками (пример In[5]). Более подробно со списками мы познакомимся в следующей лекции.
2.4. Атрибуты
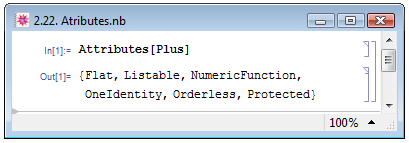
Все функции в Mathematica обладают определёнными свойствами, называемыми атрибутами. Атрибуты той или иной функции можно узнать, применив к ней функцию Attributes. Воспользуемся подходом П. Веллина и др. [14, с. 50–51] к рассмотрению некоторых атрибутов на примере функции Plus — см. рис. 2.22.
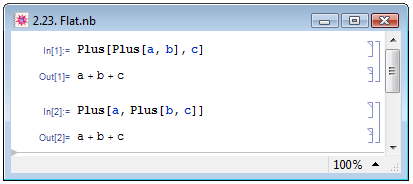
Атрибут функции Flat соответствует свойству ассоциативности. В программировании ассоциативностью (или очерёдностью) называют последовательность выполнения действий (или направление вычисления), реализуемое, когда операторы имеют одинаковый приоритет и отсутствует явное (с помощью скобок) указание на очерёдность их выполнения. На примере функции Plus понятие ассоциативности можно сформулировать более простым языком: если необходимо сложить друг с другом три элемента, то не имеет значения, какие два из них будут сложены первыми. Математическим языком это свойство можно представить как  . На примере выражений Mathematica это можно проиллюстрировать, сказав, что выражения Plus[Plus[a,b],c] и Plus[a,Plus[b,c]] эквивалентны одноуровневому выражению Plus[a,b,c]. Если Mathematica определяет ту или иную функцию как ассоциативную, она записывает её в одноуровневой форме — см. рис. 2.23.
. На примере выражений Mathematica это можно проиллюстрировать, сказав, что выражения Plus[Plus[a,b],c] и Plus[a,Plus[b,c]] эквивалентны одноуровневому выражению Plus[a,b,c]. Если Mathematica определяет ту или иную функцию как ассоциативную, она записывает её в одноуровневой форме — см. рис. 2.23.
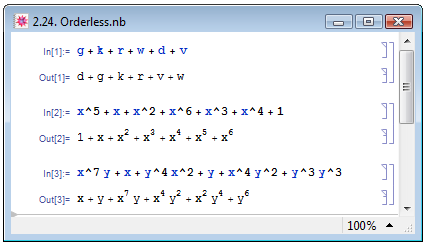
Атрибут Orderless обозначает свойство коммутативности; это означает, что для обладающей им функции не имеет значения порядок её аргументов. На примере сложения в математике это свойство можно проиллюстрировать как  . Mathematica сортирует выражения в так называемом каноническом порядке. Выражения, состоящие из букв и слов, сортируются по алфавиту (пример In[1] на рис. 2.24), степенные многочлены сортируются по степени переменной (пример In[2]). Однако, иногда сортировка, которую осуществляет Mathematica, неочевидна и диктуется исключительно нуждами программы (пример In[3]).
. Mathematica сортирует выражения в так называемом каноническом порядке. Выражения, состоящие из букв и слов, сортируются по алфавиту (пример In[1] на рис. 2.24), степенные многочлены сортируются по степени переменной (пример In[2]). Однако, иногда сортировка, которую осуществляет Mathematica, неочевидна и диктуется исключительно нуждами программы (пример In[3]).
Когда выражение имеет атрибут Protected, это означает, что пользователь не может каким-либо образом изменять это выражение. Все встроенные функции обладают этим атрибутом.
Атрибут OneIdentity означает, что повторное применение функции, обладающей этим атрибутом, к одному и тому же аргументу не будет иметь эффекта. Например, в Mathematica выражения Plus[Plus[a,b]] и Plus[a,b] будут эквивалентны друг другу.
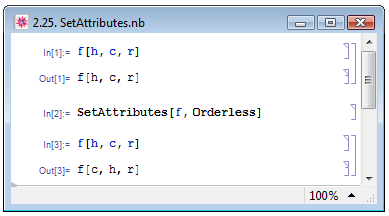
В Mathematica имеется возможность изменять атрибуты функций. И если делать это со встроенными функции кажется нерациональным и бессмысленным, то определять атрибуты для пользовательских функций может оказаться полезным. Например, имеется функция, для которой вы хотите задать атрибут Orderless. Если без этого атрибута функция не изменяет порядок собственных аргументов (см. пример In[1] на рис. 2.25), то с ним она автоматически сортирует аргументы согласно встроенным правилам сортировки (последовательно примеры In[2] и In[3]). Для задания атрибутов выражений используется функция SetAttributes[expr,a], где expr — само выражение, a — задаваемый атрибут. Для задания одновременно нескольких атрибутов функция применяется в виде SetAttributes[expr,{a1,a2,...}], где a1,a2,.. — задаваемые атрибуты.
Ключевые термины
Ассоциативность (или очерёдность) — последовательность выполнения действий (или направление вычисления), реализуемое, когда операторы имеют одинаковый приоритет и отсутствует явное (с помощью скобок) указание на очерёдность их выполнения.
Атрибуты — свойства выражений Mathematica.
Атомарными называют простейшие выражения Mathematica.
Вещественные данные — числа, которые в общем случае содержат мантиссу с разделёнными точкой целой и дробной частями и порядок, вводимый как степень числа 10.
Внутреннее представление или полная форма — это универсальная форма представления выражений, соответствующая структуре h[expr1,expr2,...], содержащей заголовок h и разделённые запятыми аргументы expr1,expr2,... в квадратных скобках
Выражениями называются любые данные, вводимые пользователем в секции Input и предназначенные для обработки ядром.
Глубина выражения — максимальный номер уровня в выражении плюс единица.
Идентификаторами называются имена переменных.
Именованная константа — выражение, которое рассматривается программой как функция без аргумента, возвращающая заранее заданное значение.
Коммутативность — свойство функции, которое означает, что наделенная им функция безразлична к порядку ее аргументов.
Константы являются типовыми объектами системы, несущими заранее предопределенное численное или символьное значение.
Логические операторы (известные также как булевы функции, булевы операторы) — выражения, определяющие правильность выражений, основных на булевой алгебре.
Оператор отношений — предикат, отражающий логическое соответствие между данными.
Машинный ноль — наименьшее число, которое воспринимается системой как ноль.
Переменными в системе Mathematica являются именованные объекты, способные в ходе выполнения документа неоднократно принимать различные значения — как численные, так и символьные.
Предикат/ — функция, возвращающая логическое значение True или False в зависимости от того, удовлетворяет или не удовлетворяет их аргумент условию проверки.
Рациональные данные — отношения целых чисел, которые представляются системой без погрешности и ограничения точности.
Символ — это последовательность букв, цифр и знака $, не начинающаяся с цифры.
Список — форма структурирования данных, по строению представляющая собой множество элементов, заключённых в фигурные скобки и разделённых запятыми.
Строка — это последовательность букв, цифр и спецсимволов, заключённая в кавычки.
Функция пользователя — набор правил, задаваемых пользователем.
Целочисленные данные — это целые числа, которые представляются системой без погрешности и ограничения разрядности.
Краткие итоги
В данной лекции мы подробно познакомились с двумя классами данных Mathematica — численными и символьными данными, а также получили начальную информацию о третьем классе данных — списках. Мы узнали об основных отличиях при задании пользователем и использовании программой целых, рациональных, вещественных и комплексных чисел. Мы познакомились с ключевым понятием Mathematica — выражением, научились задавать простейшие атомарные выражения и конструировать из них сложные выражения. Мы узнали о "двуличии" выражений Mathematica — о том, что они обладают, по меньшей мере, двумя представлениями: внутренним и внешним. Мы научились обращаться к отдельным элементам сложных выражений. Мы познакомились с такими объектами системы, как константы, переменные и пользовательские функции, и научились пользоваться ключевыми операторами системы — присваиванием и отложенным присваиванием. Мы научились проверять выражения на соответствие тем или иным условиям при помощи предикатов, в том числе, операторов отношений и логических операторов. Мы узнали о возможности придания функциям определённых свойств при помощи атрибутов и познакомились с некоторыми из них.
Вопросы
- Что называют выражением в Mathematica? Что такое атомарное выражение?
- К каким классам данных могут относиться выражения Mathematica?
- Перечислите типы численных данных, раскройте понятия, приведите примеры.
- К какому типу численных данных будет принадлежать сумма чисел вещественного и целого; рационального и комплексного; вещественного и комплексного; целого и рационального?
- Что такое символ в Mathematica? Приведите примеры символьных данных.
- Что такое строка в Mathematica?
- Какую структуру имеют выражения в Mathematica?
- Что такое внутреннее представление или полная форма выражения?
- Каким образом можно узнать внутреннюю форму произвольного выражения Mathematica?
- Какие объекты являются в Mathematica константами; переменными?
- Что такое идентификатор? Какими свойствами должен обладать идентификатор?
- Приведите примеры основных операций по присваиванию переменным значений.
- На приме поясните разницу между операциями немедленного присваивания и отложенного присваивания.
- Какие объекты Mathematica называются предикатами? Приведите примеры используемых в Mathematica предикатов.
- Для чего используются операторы отношений и логические операторы? Приведите примеры операторов.
- Что такое список в Mathematica?
- Что такое атрибуты функций Mathematica? Приведите примеры атрибутов.
Упражнения
- Представьте в полной форме выражения a*x^2+b*x+c, Log[p+q*r], x^y^z.
- Каково традиционное представление заданных в полной форме выражений Power[Plus[x,Log[Plus[x,y]]],2], Plus[a,Power[b,2],Times[-1,Power[c,3]],Power[d,4]], Plus[x,Times[-1,Power[x,y]],Times[2,x,y]]?
- При помощи функции Head определите тип следующих выражений: 123, 15.46, sometext, "sometext", I+6, {1,a}.
- Создайте список, элементами которого являются только символьные данные; только численные данные; только списки.
- Введите в окно редактирования ваше имя, определите тип введённого выражения. Обособьте имя кавычками " ", определите тип полученного выражения. Создайте список, в качестве элементов которого укажите ваши имя, отчество и фамилию.
- Выведите на экран надпись "I learn Mathematica", чтобы каждое слово начиналось с новой строки.
- Проверьте, являются ли числа 27, 91, 127, 417, 523 простыми.
- Сравните между собой выражения
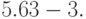 и
и  ,
, 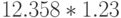 и
и  ,
, 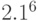 и
и 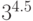 .
. - Выясните, какими атрибутами обладают функции ListPlot, Sqrt, Sin, Power.