Классы данных в Mathematica
2.2. Символьные данные
2.2.1. Символы и строки
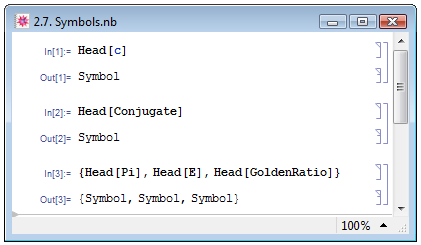
Символы, как сказано выше, относятся к атомарным выражениям. Символы — это последовательность букв, цифр и знака $, не начинающаяся с цифры (Е. М. Воробьёв [1, с. 15]). Например, и буква с, и слово Conjugate являются символами. Убедиться в этом несложно, воспользовавшись уже известной нам функцией Head — см. рис. 2.7. Кроме того, символами в Mathematica являются именованные или "поименованные константы, которые можно рассматривать как функции без аргумента, возвращающие заранее заданное значение" (В. П. Дьяконов [2, с. 167]). Список некоторых именованных констант Mathematica см. на рис. 2.8.
Символьные данные В. П. Дьяконов [2, с. 163] описывает следующим образом: "Символьные данные в общем случае могут быть отдельными символами (например, a, b,...,z), строками (strings) и математическими выражениями expr (от expression – выражение), представленными в символьном виде".
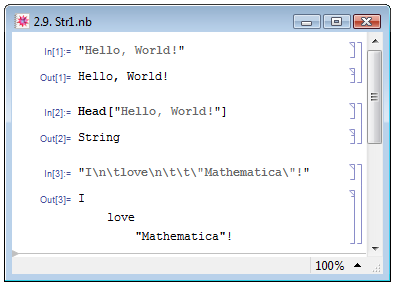
Определение строки в Mathematica даёт Е. М. Воробьёв [1, с. 15]: "Строки — это заключённые в кавычки последовательности букв, цифр и специальных символов". Строки, так же, как числа и символы, относятся к атомарным выражениям. Строки могут также содержать в себе управляющие символы, такие, как \" — кавычки (если они используются не для создания строки, а находятся внутри строки), \n — переход на новую строчку, \t — табуляция и др. Отметим, что "управляющие символы не печатаются принтером и не отображаются дисплеем, а лишь заставляют их выполнять назначенные ими действия" (В. П. Дьяконов [2, с. 163]). Функции Mathematica для работы со строками, которые будут описаны в следующей лекции. Несколько примеров работы со строками см. на рис. 2.9.
2.2.2. Выражения
Все выражения, и атомарные, и сложные, имеют одну и ту же многоуровневую структуру h[expr1,expr2,...]. Более полно структура выражений Mathematica обсуждается в книге Е. М. Воробьёва [1, с. 113]. На нулевом уровне этой структуры находится заголовок выражения h, на первом уровне — выражения expr1,expr2..., на втором уровне — элементы выражений expr1,expr2.... Е. М. Воробьёв [1, с. 115] пишет: "Глубина выражения численно равна максимальному номеру уровня в выражении плюс единица и является значением функции Depth".
Выражениями являются как заголовок функции, так и её элементы. Базовыми структурными элементами, "кирпичиками" для построения всех выражений являются атомарные выражения.
Если вы не уверены, является выражение перед вами атомарным или сложным, Mathematica позволит легко это проверить при помощи функции AtomQ. Если некоторое выражение expr является атомарным, результат вычисления функции AtomQ[expr] будет True, в ином случае — False.
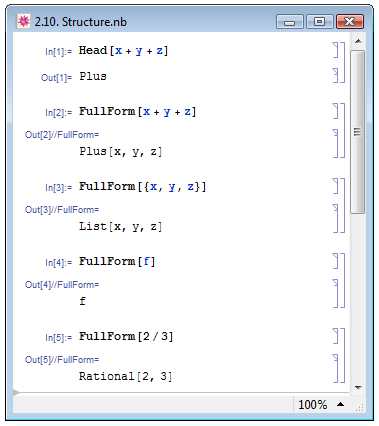
Заметим, что используемая нами ранее функция Head для определения типа атомарных выражений применительно к сложным выражениям даёт лишь их заголовок — пример In[1] на рис. 2.10. Для того чтобы увидеть выражение в так называемом внутреннем представлении, следует воспользоваться командой FullForm — примеры In[2] и In[3]. Однако применение функции к атомному выражению даёт на выходе само это выражение — примеры In[4] и In[5]. Внутреннее представление или полная форма — это универсальная форма представления выражений, соответствующая структуре h[expr1,expr2,...], содержащей заголовок h и разделённые запятыми аргументы expr1,expr2,... в квадратных скобках. Именно полная форма непосредственно воспринимается ядром системы. Пользователь же при вводе данных задаёт внешнюю форму: она зачастую может совпадать с внутренней.
Подробней о внутренней форме выражений см. книгу Е. М. Воробьёва [1, с. 113].
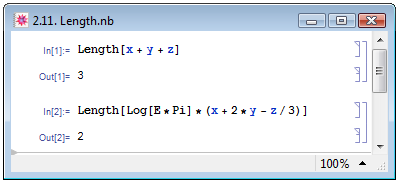
Число элементов в выражении определяет его длину, при этом элементом может являться и атомарное выражение, и сложное выражение, и некоторое сочетание сложных и атомарных выражений. В примере In[2] на рис. 2.11, несмотря на большое количество выражений в истинном для Mathematica смысле (здесь одновременно присутствуют сложение и вычитание, умножение и деление, а также нахождение логарифма), число элементов, определяющих длину основного выражения, равняется всего двум, поскольку одним элементом является извлечение логарифма, а вторым — набор действий в скобках.
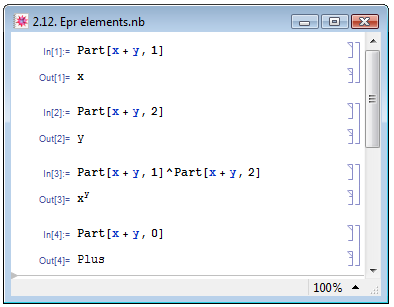
Помимо определения числа элементов выражения Mathematica позволяет отдельно обращаться к каждому из этих элементов. Для этих целей служит функция Part[expr,i], где expr — само выражение, i — номер элемента, к которому необходимо обратиться — примеры In[1], In[2] и In[3] на рис. 2.12. При этом нулевым элементом является заголовок выражения — пример In[4].
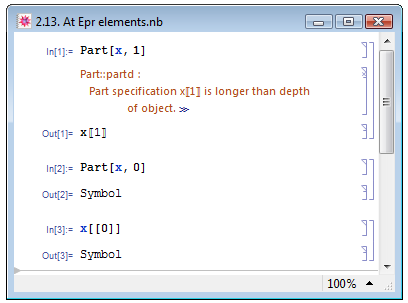
Атомарные выражения не даром имеют такое название: в их структуре нет составных элементов, поэтому при попытке обратиться к первому или следующему элементам атомарного выражения Mathematica будет выдавать ошибку, а обращение к нулевому элементу даст на выходе тип выражения, так же, как и функция Head — см. рис. 2.13.
В примере In[3] рисунка 2.13 продемонстрирован ещё один способ обращения к отдельным элементам выражения: expr[[i]], где expr — само выражение, i — номер элемента, к которому необходимо обратиться.
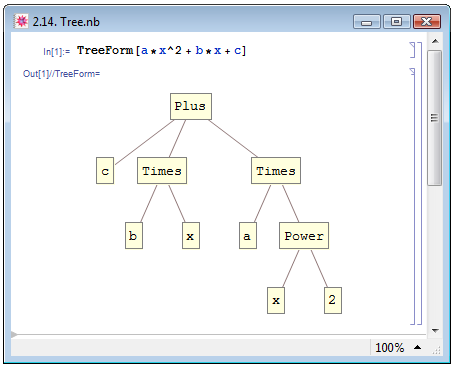
Наконец, у пользователя может возникнуть необходимость представить некоторые достаточно громоздкие сложные выражения более наглядно во внутренней форме. В этом поможет функция TreeForm, из названия которой должно быть понятно, что она позволяет представить структуру в виде дерева. П. Веллин и др. [14, с. 37] приводит следующий пример для иллюстрации этой возможности Mathematica: мы задаём выражение TreeForm[a*x^2+b*x+c] и на выходе получаем "дерево" с "корнем" в виде заголовка Plus, тремя ветвями, описывающими выражения c, b*x и a*x^2, последняя из которых, в свою очередь, сама имеет ответвление — возведение в степень, — см. рис. 2.14.
Е. М. Воробьёв [1, с. 116] выделяет четыре основных способа интерпретации выражений:
- Заголовок h выражения есть название математической функции, например Log, а элементы выражения — аргументы этой функции.
- Заголовок понимается как команда, например, Simplify, а элементы — как ее адресаты.
- Заголовок как оператор (Integrate, Plus), применяемый к операндам.
- Заголовок как указание на тип данных (List, Integer).