Классы данных в Mathematica

2.2.3. Константы, переменные и функции пользователя

Одна из ключевых возможностей, один из атрибутов любой среды программирования — возможность определять функции, константы и процедуры. Более подробно мы коснёмся этих вопросов в лекциях настоящего курса, посвящённых программированию, здесь приведём лишь сведения общего характера и простейшие примеры.

В процессе выполнения расчётов часто может встретиться ситуация, когда возникает потребность в использовании функции, которой нет среди встроенных в Mathematica. Также не является редкостью и ситуация, когда приходится многократно пользоваться одним и тем же выражением. В обоих случаях сослужит добрую службу возможность самостоятельно определять выражения, обращение к которым в тексте программы вызывает выполнение заданного набора операций. Таким способом выражениям можно присваивать константы, переменные и функции пользователя.

Такому объекту, как константы, В. П. Дьяконов [2, с. 167] даёт следующее определение: "Константы являются типовыми объектами системы, несущими заранее предопределенное численное или символьное значение". Это значение не меняются по ходу вычисления документа. К численным константам относятся любые числа, непосредственно используемые в выражениях. Так, числа 1 и 2 в выражении 2*Cos[1] являются численными константами. В роли идентификатора численной константы выступает само число. В отличие от численных констант, именованные константы имеют собственные идентификаторы

В. П. Дьяконов [2, с. 168] пишет, что "переменными в системе Mathematica являются поименованные объекты, которые в ходе выполнения документа могут неоднократно принимать различные значения – как численные, так и символьные. При этом символьные значения переменных, в отличие от обычных языков программирования, могут представлять собой как исполняемые математические выражения expr, так и некоторые обобщенные классы функций и объектов. Например, переменная может представлять графический объект, такой как изображение трехмерной поверхности, или звуковой объект, при активизации которого исполняется звук. Значением переменных могут быть также и множественные объекты-списки".

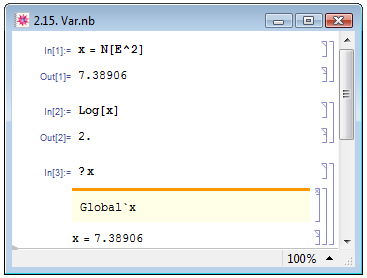
Для того, чтобы узнать присвоенное ранее значение некоторой переменной expr, следует воспользоваться уже известной нам функцией вызова справки ?expr. На рис. 2.15. представлены примеры задания переменных (In[1]), обращения к ним в процессе расчётов (In[2]) и получения информации о присвоенных значениях (In[3]).

Рис. 2.15. Задание переменных и работа с ними

В книге В. П. Дьяконова [2, с. 169] даётся понятие идентификаторов переменных: "Имена переменных называют их идентификаторами". — Также оговариваются правила их задания. Так идентификаторы переменных должны быть уникальными: для принципиальной возможности осуществления вычислений они не должны совпадать с именами директив, атрибутов, опций и функций, а также для возможности получения корректных результатов разные переменные должны иметь отличные друг от друга идентификаторы.

Имена переменных должны начинаться с буквы. Задавать тип переменной заранее ненужно: Mathematica сама это сделает в требующийся момент.

Переменные в системе Mathematica являются глобальными, то есть, задать и изменить значение переменной можно в любом месте программы. В результате вычисления выражения var=expr переменной var присваивается значение expr. Ниже представлены основные операции по присваиванию переменным значений (В. П. Дьяконов [2, с. 169–170]).

х = expr — происходит присвоение переменной х вычисленного значения expr;

х = у = expr — присвоение вычисленного значения expr происходит переменным х и у;

x:=expr — переменной х присваивается невычисленное значение expr;

х =. — с переменной х снимается определение.

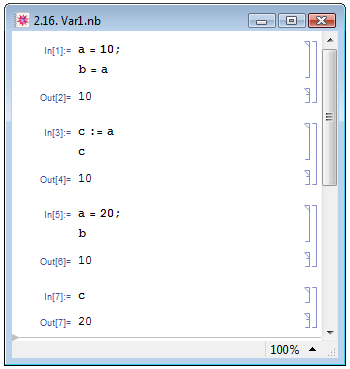
На рисунке 2.16 пояснена разница между оператором присваивания " = " и оператором отложенного присваивания " := ". После первоначальных присваиваний b=а и с:=а обе переменные, b и с, имеют значение 10. Однако после присваивания переменной а нового значения (20) переменная b, которой было присвоено вычисленное значение а, остается равной 10, а переменная с, которой было присвоено невычисленное значение а, становится равной 20.

Крайне важна возможность снятия с переменной определения с помощью оператора " =. " или функции Clear[var]. Это крайне важно, поскольку переменные с одним и тем же именем могут использоваться в совершенно разных целях в разных частях программы. Более того, эти объекты сохраняются даже при работе с другим документом Mathematica. Поэтому рекомендуется всякий раз удалять определения переменных, как только их использование завершается. Во-первых, это уменьшает вероятность получения неадекватных результатов расчётов, и, во-вторых, освобождает память.

Рис. 2.16. Различие между операторами присваивания и отложенного присваивания

О следующем инструменте системы Mathematica В. П. Дьяконов [2, с. 173] пишет следующее: "Хотя в систему входят сотни встроенных функций (начиная от элементарных и кончая специальными математическими функциями и системными функциями), нередко требуется расширить её вводом новых функций, действие которых задаётся пользователем. Такие функции принято называть функциями пользователя".

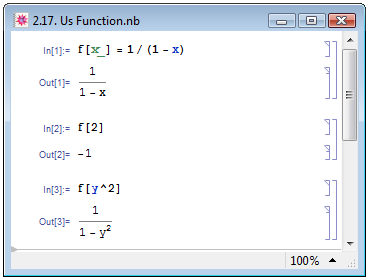
Для задания функции f необходимо воспользоваться следующей конструкцией: f[x_], где выражение в квадратных скобках x_ обозначает переменную, которая будет подставлена в правую часть функции вместо x. Более подробно о пользовательских функциях мы поговорим в лекции, посвящённой функциональному программированию. Здесь приведём пример задания некоторой пользовательской функции и её выполнения для некоторой переменной — см. рис. 2.17.

Рис. 2.17. Работа с пользовательскими функциями.

2.2.4. Предикаты

При работе с данными часто возникает необходимость проверить, удовлетворяет ли то или иное выражение некоторому критерию, условию. Для этих целей в Mathematica существуют конструкции, позволяющие тестировать данные на удовлетворение тем или иным условиям. Подобные конструкции называются предикатами. Предикат — функция, возвращающая логическое значение True или False в зависимости от того, удовлетворяет или не удовлетворяет их аргумент условию проверки (П. Веллин и др. [14, с. 45]). Приведём предикаты, наиболее часто используемые в Mathematica.

• PrimeQ[expr] — проверяет, является ли аргумент expr простым числом,
• EvenQ[expr] — чётным числом,
• OddQ[expr] — нечётным числом,
• IntegerQ[expr] — целым числом;
• NumericQ[expr] — принимает ли аргумент expr численное значение;
• AtomQ[expr] — является ли выражение в аргументе expr атомарным,
• ListQ[expr] — списком,
• MatrixQ[expr] — вложенным списком второго уровня (матрицей);
• IntervalMemberQ[Interval[{l,r}],expr] — лежит ли выражение expr в интервале от l до r;
• PolynomialQ[expr1,expr2] — является ли выражение expr1 полиномом относительно выражения expr2.

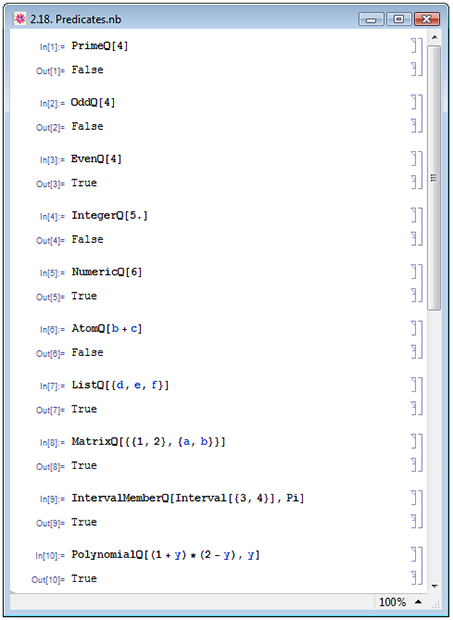
Примеры, иллюстрирующие действие приведённых выше функций, представлены на рис. 2.18.

увеличить изображение
Рис. 2.18. Использование предикатов в Mathematica

2.2.5. Операторы отношений и логические операторы

Существует ряд предикатов, выделенных в отдельную группу операторов отношений. В. П. Дьяконов [2, с. 183] пишет: "Логическими принято называть операции, отражающие чисто логическое соответствие между данными. В математике (да и в информатике) принято характеризовать логическое соответствие утверждениями True (Верно или Да) и False (Неверно или Нет). Слова True и False являются символьными константами, отражающими результаты логических операций и в системе Mathematica".

В Mathematica операторы отношений задаются следующим образом:

• Equal[expr1,expr2] (или expr1==expr2) — равно,
• Unequal[expr1,expr2] (или expr1!=expr2) — неравно,
• Greater[expr1,expr2] (или expr1<expr2) — больше,
• Less[expr1,expr2] (или expr1<expr2</expr2) — меньше,
• GreaterEqual[expr1,expr2] (или expr1>=expr2) — больше или равно,
• LessEqual[expr1,expr2] (или expr1<=expr2) — меньше или равно.

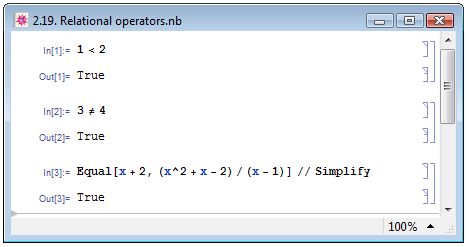
Несколько примеров использования операторов отношений представлено на рис. 2.19.

Рис. 2.19. Операторы отношений в Mathematica

Логические операторы (известные также как булевы функции, булевы операторы) определяют правильность выражений, основных на булевой алгебре (П. Веллин и др. [14, с. 47]).

Логические операторы задаются следующим образом:

• Not[expr] или !expr — логическое отрицание,
• And[expr1,expr2,...] или expr1&&expr2&&... — логическое умножение, операция "И" ,
• Or[expr1,expr2,...] или expr1||expr1||... — логическое сложение, операция "ИЛИ"
• Xor[expr1,expr2,...] или (expr1||expr1)&&!(expr1&&expr1) — сложение по модулю 2, операция "исключающее ИЛИ".

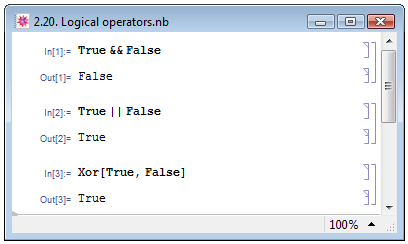
На рис. 2.20 приведены примеры использования логических операторов.

Рис. 2.20. Логические операторы в Mathematica