Работа с числами
Цель лекции: Познакомиться с особенностями представления численных данных в Mathematica и работы с ними.
4.0. Введение
Главным отличием Mathematica от других вычислительных систем, таких, как калькуляторы, традиционные языки программирования и иные системы вычислений, является возможность эффективной работы с символьными данными. Однако заслуживает внимания и иная возможность пакета, которая роднит его со всеми программами для математических расчетов — умение эффективно работать с численными данными. В большинстве языков программирования перед началом работы с той или иной функцией, следует сначала задавать тип числовых данных. Mathematica самостоятельно улаживает подобные детали: однако понимание особенностей работы программы с разными типами данных поможет раскрыть все её возможности и сделать вычисления более эффективными. Для знакомства с принципами задания чисел в Mathematica и работы с ними за основу возьмём книгу П. Веллина и др. [14].
4.1. Типы численных данных
Первое, что мы сделаем в этой лекции — вспомним типы чисел, с которыми работает Mathematica.
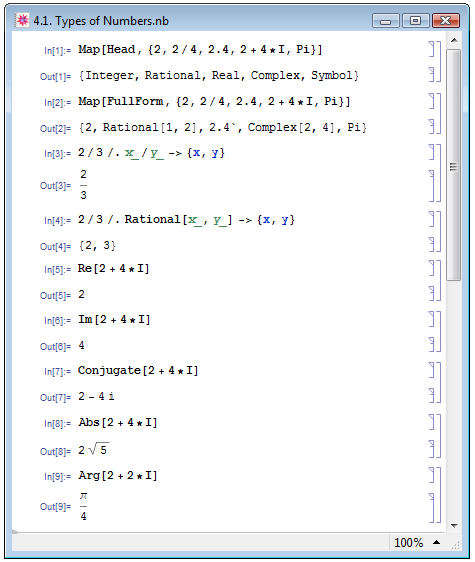
В лекции 2 настоящего курса мы узнали, что в Mathematica существуют четыре типа чисел: целые, рациональные, вещественные и комплексные. Также мы узнали, что числа являются атомарными выражениями, то есть, они не состоят из выражений более низкого уровня. На рисунке 4.1 даны примеры In[1] и In[2] определения типа числа при помощи функции Head[expr] и представления чисел во внутренней форме при помощи FullForm[expr].
Целые числа являются точными и записываются без точки в десятичной дроби. Рациональные числа задаются отношением целых чисел и также рассматриваются программой как точные. Знание внутреннего представления рационального числа может оказаться крайне необходимым при проведении вычислений. Воспользуемся подходом П. Веллина и др. [14, с. 224], в котором он демонстрирует пользу знания внутреннего представления чисел в Mathematica. Пусть из некоторого набора данных необходимо выбрать только рациональные числа. В этом случае следует прибегнуть к использованию шаблонов (pattern matching) — выражений вида x_ (подробней с использованием шаблонов мы познакомимся в лекции, посвящённой функциональному программированию). Однако если мы зададим для поиска шаблон x_/y_, то требуемого результата не добьемся (пример In[3] на рис. 4.1), а анализ по шаблону, заданному функцией Rational[x_,y_], однозначно позволит провести требуемые действия именно с рациональными числами (пример In[4]).
Все числа, содержащие десятичную точку, называются в Mathematica вещественными. Они рассматриваются программой как приближённые. Например, числа 5 и 5.0, кажущиеся пользователю одинаковыми, в Mathematica имеют совершенно разно представление и разные алгоритмы обработки.
Комплексные числа задаются в виде 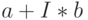 , где
, где  — мнимая единица, квадратный корень из
— мнимая единица, квадратный корень из 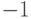 . Числа
. Числа  и
и  могут быть целыми, рациональными или вещественными, и в зависимости от этого комплексное число будет рассматриваться как точное (в первых двух случаях) или как приближённое (в последней случае). Внутренняя форма записи комплексного числа — Complex[a,b]. Действительная и мнимая части комплексного числа
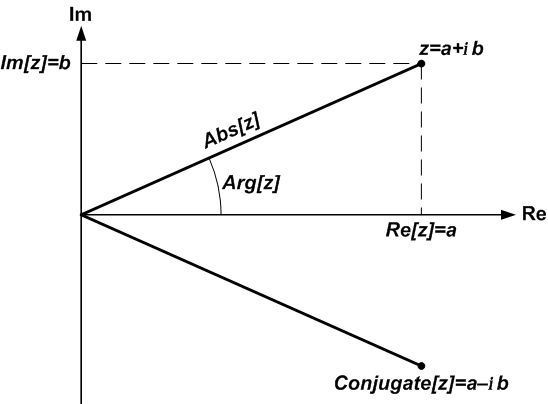
могут быть целыми, рациональными или вещественными, и в зависимости от этого комплексное число будет рассматриваться как точное (в первых двух случаях) или как приближённое (в последней случае). Внутренняя форма записи комплексного числа — Complex[a,b]. Действительная и мнимая части комплексного числа  выделяются при помощи функций Re[z] и Im[z], соответственно (примеры In[5] и In[6] на рис. 4.1). При помощи функций Conjugate[z] и Abs[z] находят комплексно сопряжённое к z число и абсолютное значение z, соответственно (примеры In[7] и In[8]). При помощи функции Arg[z] задаётся угол наклона радиус-вектора точки z на комплексной плоскости (пример In[9]). На рис. 4.2. геометрически проиллюстрированы все параметры комплексных чисел, определяемые при помощи указанных выше функций. Иллюстрацию, благодаря её наглядности, мы позаимствовали в работе П. Веллина и др. [14, с. 232].
выделяются при помощи функций Re[z] и Im[z], соответственно (примеры In[5] и In[6] на рис. 4.1). При помощи функций Conjugate[z] и Abs[z] находят комплексно сопряжённое к z число и абсолютное значение z, соответственно (примеры In[7] и In[8]). При помощи функции Arg[z] задаётся угол наклона радиус-вектора точки z на комплексной плоскости (пример In[9]). На рис. 4.2. геометрически проиллюстрированы все параметры комплексных чисел, определяемые при помощи указанных выше функций. Иллюстрацию, благодаря её наглядности, мы позаимствовали в работе П. Веллина и др. [14, с. 232].
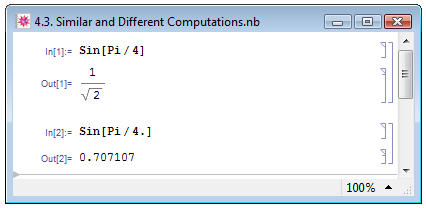
Акцентируем внимание на том, что при работе с разными типами чисел различаются не только способы представления результатов вычислений, но и применяемые программой алгоритмы вычислений (см. книгу П. Веллина и др. [14, с. 221]). В примерах на рис. 4.3 мы вычисляем синус от угла 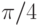 . В примере In[1], где мы задали в знаменателе целое число 4, Mathematica ищет среди встроенных правил преобразований соответствие заданного выражения с сочетанием функции Sin и выражения Pi/4. В случае успеха она применяет правило преобразования, и в конечном итоге выдаёт алгебраический (точный) результат (см. Out[1]). В примере In[2], поскольку мы изначально задали вещественное, т. е., заведомо неточное число 4.0, конечное выражение находится численно с той же точностью, что и исходное (Out[2]).
. В примере In[1], где мы задали в знаменателе целое число 4, Mathematica ищет среди встроенных правил преобразований соответствие заданного выражения с сочетанием функции Sin и выражения Pi/4. В случае успеха она применяет правило преобразования, и в конечном итоге выдаёт алгебраический (точный) результат (см. Out[1]). В примере In[2], поскольку мы изначально задали вещественное, т. е., заведомо неточное число 4.0, конечное выражение находится численно с той же точностью, что и исходное (Out[2]).
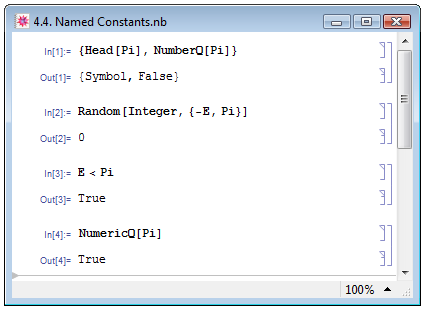
В последнем примере во входных данных для вычисления мы использовали особое выражение Pi. Это выражение относится к известным нам из второй лекции именованным константам и осуществляет обращение к числу  . Оно, равно как и другие именованные константы, имеет "двойственную природу" (П. Веллин и др. [14, с. 226]). С одной стороны, оно рассматривается Mathematica не как число, а как символ, что подтверждается примером Out[1] на рис. 4.4. С другой же стороны, сама Mathematica оперирует им как обычным вещественным числом — примеры In[2] и In[3]. Для того чтобы программа могла использовать константы как числа, они имеют специальный атрибут — NumericQ, означающий их численную природу, несмотря на внешнюю форму — пример In[4].
. Оно, равно как и другие именованные константы, имеет "двойственную природу" (П. Веллин и др. [14, с. 226]). С одной стороны, оно рассматривается Mathematica не как число, а как символ, что подтверждается примером Out[1] на рис. 4.4. С другой же стороны, сама Mathematica оперирует им как обычным вещественным числом — примеры In[2] и In[3]. Для того чтобы программа могла использовать константы как числа, они имеют специальный атрибут — NumericQ, означающий их численную природу, несмотря на внешнюю форму — пример In[4].