Работа с числами
4.4.2. Представление приближённых чисел
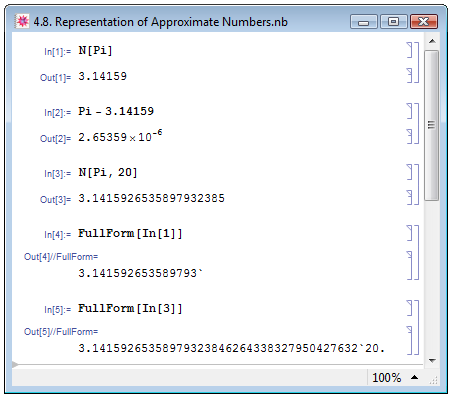
Автоматически, без особых указаний Mathematica при работе с действительными числами выводит на экран шесть значащих цифр числа (пример In[1] на рис. 4.8). Однако это не значит, что в дальнейших вычислениях будут использоваться только показанные пользователю цифры. В примере In[2] (аналогичном примеру из книги П. Веллина и др. [14, с. 237]) мы вычтем из истинного значения числа 
его приближённое значение, выведенное на экран, и в результате получим отличный от нуля результат: это прекрасно иллюстрирует тот факт, что внутреннее значение числа отлично от выведенного на экран.
На основе уже полученных в этой лекции знаний мы, наконец, можем разобраться в том, как работает неоднократно использованная нами в предыдущих лекциях функция N[expr]: сначала она преобразовывает заданное действительное число в число с машинной разрядностью, а затем выводит шесть его значащих цифр. Дальнейшие вычисления с этим числом происходят с машинной разрядностью.
Однако при помощи функции N можно вывести на экран численное значение величины и с самостоятельно заданной разрядностью: для этого следует добавить в функцию N второй аргумент, определяющий число значимых цифр в результате вычисления. В примере In[3] на рис. 4.8 мы задали значение разрядности, равное 20.
Внутреннее представление числа num, заданного с некоторой разрядностью, можно узнать при помощи уже известной нам функции FullForm[num]. Если результат вычислений завершается знаком " ' " (пример Out[4] на рис. 4.8), это означает, что число задано с машинной разрядностью; в противном случае число, указанное после знака " ' " означает его разрядность (пример Out[5]).
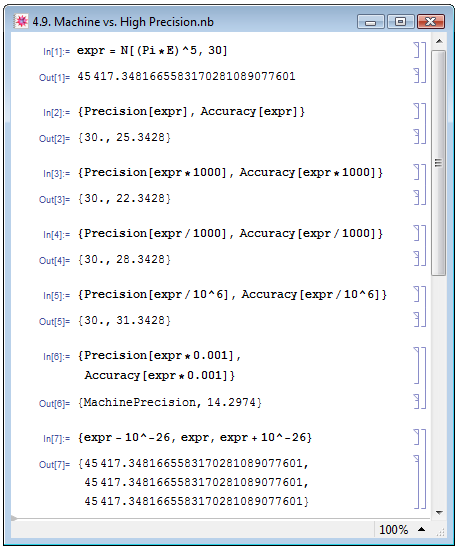
Посмотрим теперь, что происходит с разрядностью и точностью при выполнении вычислений. Для этого воспользуемся подходом П. Веллина и др. [14, с. 236]. В примере In[1] на рис. 4.9 мы присвоили выражению expr значение некоторого числа с разрядностью 30, а в примере In[2] мы, во-первых, убедились в том, что его разрядность имеет значение 30, а также определили точность, с которой оно задано. Поскольку перед разделительной точкой в Out[1] стоят значащие цифры, то неудивительно, что разрядность по величине больше точности. Передвинем разделительную точку в выражении expr вправо на 3 разряда, домножив его на 1000, и определим разрядность и точность полученного выражения — пример In[3]. Как мы видим, разрядность не изменилась вовсе, зато точность уменьшилась на 3: это объясняется тем, что в дробной части стало на 3 значащих цифры меньше, чем раньше. Противоположного результата, то есть, увеличения точности мы добьёмся, передвинув в исходном выражении точку влево — пример In[4].
Чем левее мы будем передвигать десятичную точку, тем больше будет величина точности. В тот момент, когда перед разделительной точкой больше не останется значащих цифр, точность по величине превзойдёт разрядность. Убедимся в этом, передвинув в исходном выражении точку влево на 6 разрядов — пример In[5] на рис. 4.9.
Следует акцентировать внимание на том, что в примерах In[2], In[4] и In[5] на рис. 4.9 мы переносили десятичную точку, деля или умножая исходное выражение на точные (целые) числа. Осуществление подобных математических операций с заданным с машинной разрядностью вещественным числом приведёт к изменению разрядности всего результата на машинную и соответствующему изменению точности. В примере In[6] вместо того, чтобы разделить исходное выражение на точное (целое) число 1000, мы умножили его на приближённое (вещественное) 0.001. Результат Out[6] подтверждает сказанное ранее.
Таким образом, разрядность, определяющая количество значащих цифр, от положения десятичной точки не зависит, в то время как точность изменяется при изменении положения точки и может быть как меньше, так и больше разрядности.
Теперь узнаем, каким образом Mathematica определяет разрядность и точность, и почему эти числа зачастую не являются целыми.
Пусть задано приближенное значение вещественного числа 
с погрешностью 
. Mathematica считает, что число лежит в интервале 
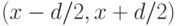, длина которого равна погрешности . Тогда разрядность числа определяется по формуле 
, а точность — по формуле 
. Таким образом, число, заданное с точностью a имеет погрешность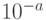 
, в то же время погрешность отличного от нуля числа с разрядность 
имеет погрешность 
. В справедливости данного определения можно убедиться в книге С. Вольфрама [15, Часть 3, Глава 3.1, с. 7].
Если прибавить к числу или вычесть из него величину, меньшую погрешности, в представлении на экране это не будет иметь никакого эффекта — пример In[7] на рис. 4.9.
Подробней разрядности и точности чисел см. книги Е. М. Воробьёва [1, с. 65–67] П. Веллина и др. [14, с. 234–242].
4.4.3. Опции функций для управления точностью и разрядностью вычислений
Встроенные функции Mathematica для выполнения численных расчётов (назовём их для простоты численные функции) разработаны с учётом баланса между точностью и затраченным на вычисления временем: чтобы результаты вычислений имели наибольшую точность при минимальном затрачиваемом на получение результатов времени. Для контроля разрядности и точности вычислений встроенные функции Mathematica имеют ряд опций, с которыми мы познакомимся ниже (П. Веллин и др. [14, с. 254]).
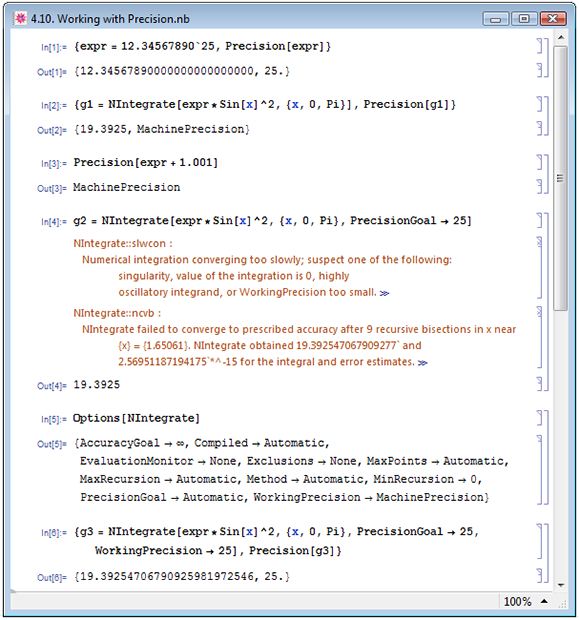
Если применить некоторую численную функцию к произвольному вещественному числу, вычисления будут проведены с машинной разрядностью. В примере In[1] на рис. 4.10 мы присваиваем выражению expr некоторое действительное число, причём величину его разрядности задаём 25. В том же примере мы убеждаемся, что разрядность числа действительно имеет значение 25. В примере In[2] мы при помощи функции NIntegrate[fun[var],{var,a,b}], где fun[var] — интегрируемая функция от переменной var, a и b — пределы интегрирования, проводим численное интегрирование некоторой математической функции expr*Sin[x] от переменной x, изменяющейся в пределах от 0 до Pi. В том же примере мы узнаём, что результат интегрирования был получен с машинной разрядностью. Таким образом, при проведении расчёта с некоторой численной функцией результат вычисления будет получен с машинной разрядностью. Также результат с машинной разрядностью будет получен при выполнении простейших математических операций с несколькими числами, хотя бы одно из которых задано с машинной разрядностью — пример In[3] на рис. 4.10.
Если всё жё требуется получить результат с большей разрядностью, следует использовать при записи численной функции опцию, задаваемую в виде PrecisionGoal->p, где p — значение задаваемой разрядности. В примере In[4] на рис. 4.10 мы осуществим то же действие, что и в примере In[2], но используем опцию задания разрядности вычислений. Однако в Out[4] Mathematica выдала нам сообщение о том, что произвести вычисление с заданной разрядностью невозможно. Если при помощи Options[funchead] мы выведем на экран значений всех опций функции с заголовком funchead (в нашем примере это NIntegrate), то увидим, что другая опция WorkingPrecision имеет значение по умолчанию, которое равно машинной разрядности (пример In[5]). Это значит, что, несмотря на нашу заявку получить результат с заданной разрядностью, алгоритм вычисления будет работать с машинной разрядностью. Чтобы всё-таки получить требуемый результат, нужно также изменить и значение опции WorkingPrecision, присвоив ему значение, равное или чуть большее, чем PrecisionGoal — см. пример In[6].
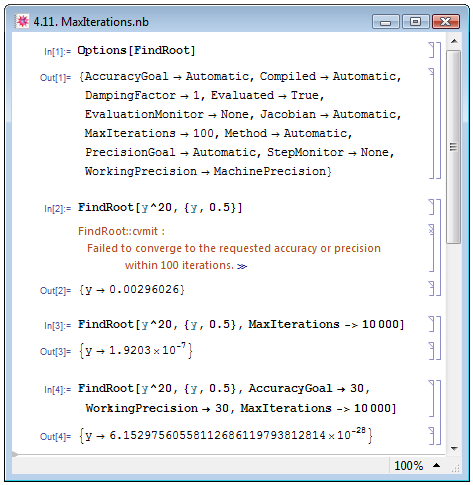
Ещё одна опция численных функций — MaxIterations. Как становится понятно из заголовка, эта функция задаёт максимальное количество повторений, выполняемых заданной итерационной функцией в процессе вычислений. Как и П. Веллин и др. [14, с. 255–256], рассмотрим эту опцию на примере функции FindRoot[expr,{var,var0}], ищущей итерационным методом значение переменной var, обращающей выражение expr в 0; на первой итерации var принимает значение var0. Как мы видим в примере In[1] на рис. 4.11, значение MaxIterations по умолчанию равно 100. Для большинства вычислений этой величины достаточно, но может возникнуть необходимость повысить число повторений.
Сравним примеры In[2] и In[3] на рис. 4.11 нахождения нуля функции 
, при этом, в первом случае используем автоматическое значение MaxIterations, а во втором случае значительно повысим его. Мы видим, что во втором случае результат оказывается значительно — на несколько порядков — ближе к искомому точному результату (который, как мы знаем, есть число 0). В Out[2] Mathematica выдала сообщение о том, что при заданном числе повторений (в нашем случае это автоматически заданная величина 100) не удаётся найти удовлетворительное при заданной (машинной) точности значение переменной. Поэтому повысить точность вычислений попробуем также, увеличив значение опции AccuracyGoal (пример In[4]). Эта опция оказывает такое же влияние на точность вычислений, как опция PrecisionGoal — на разрядность, и точно также взаимодействует с опцией WorkingPrecision. В Out[4] получаем значение, ещё более близкое к точному.
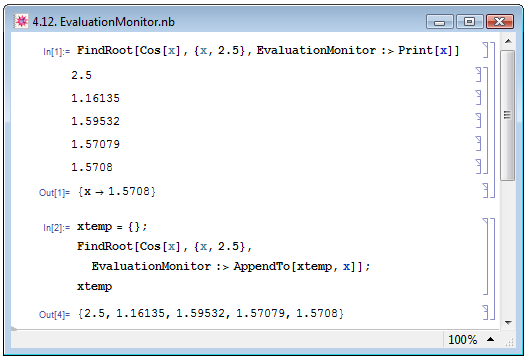
Последняя опция численных функций, с которой мы познакомимся в данной лекции, — EvaluationMonitor. Она позволяет "наблюдать" за выражением в процессе вычислений. Опишем способы её использования, предложенные П. Веллином и др. [14, с. 255–256].
Скажем, вам потребовалось получить каждое промежуточное значение выражения x, которое функция FindRoot[Cos[x],{x,2}] находит в процессе вычисления. Один из способов — выводить промежуточные значения x при помощи команды Print[x], определив её в опции EvaluationMonitor — см. пример In[1] на рис. 4.12. Однако в этом случае вы сможете только увидеть эти промежуточные значения. Для того чтобы была возможность в дальнейшем оперировать промежуточными значениями, следует прибегнуть к иному способу. Сначала нужно присвоить некоторому выражению пустой список: xtemp={}. Затем, задавая функцию FindRoot, определить для опции EvaluationMonitor следующее выражение: AppendTo[xtemp,x], — которое будет добавлять в список xtemp всё новые и новы значения x, получаемые в процессе вычисления — пример In[2]. Результат вычисления будет содержать одноуровневый список, элементами которого будут промежуточные значения вычисления итерационной функции FindRoot (Out[2]).
Подробней об управлении точностью и разрядностью вычислений см. книгу П. Веллина и др. [14, с. 254–257].
