Нечеткие множества
6.6 Меры нечеткости
Пусть  — универсальное множество. Очевидно, что "самое четкое" его подмножество — это обычное множество, функция принадлежности (характеристическая функция) которого принимает значения 0 или 1. "Самое нечеткое" подмножество — это множество, состоящее из точек перехода, в которых функция принадлежности принимает значение 0,5:
— универсальное множество. Очевидно, что "самое четкое" его подмножество — это обычное множество, функция принадлежности (характеристическая функция) которого принимает значения 0 или 1. "Самое нечеткое" подмножество — это множество, состоящее из точек перехода, в которых функция принадлежности принимает значение 0,5: 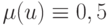 . Мера нечеткости, размытости нечеткого множества
. Мера нечеткости, размытости нечеткого множества  определяется как расстояние от этого множества до ближайшего к нему обычного множества
определяется как расстояние от этого множества до ближайшего к нему обычного множества 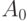 , независимо от того, какая метрика (линейная или евклидова) при этом использована. Обозначим эту величину
, независимо от того, какая метрика (линейная или евклидова) при этом использована. Обозначим эту величину  :
:
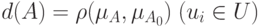 |
( 6.8) |
При этом, выполняются следующие соотношения
-
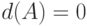 тогда и только тогда, когда
тогда и только тогда, когда  – обычное множество;
– обычное множество; -
 принимает максимальное значение тогда и только тогда, когда
принимает максимальное значение тогда и только тогда, когда 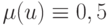 .
. -
Если имеются два нечетких множества
 и
и  и при любом
и при любом  , функции принадлежности связаны соотношениями:
, функции принадлежности связаны соотношениями: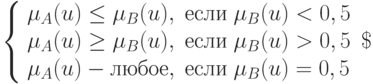 ,
,тогда
 .
. -
Симметричность относительно точки перехода, в которой функции принадлежности принимают значение 0,5. Если
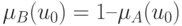 , тогда
, тогда  .
.
Чтобы с помощью  можно было сравнивать нечеткие множества, имеющие различные носители, надо нормировать
можно было сравнивать нечеткие множества, имеющие различные носители, надо нормировать  , потребовав, чтобы для любого множества мера нечеткости не превышала какой-то определенный порог, например, 1. Нормированное расстояние
, потребовав, чтобы для любого множества мера нечеткости не превышала какой-то определенный порог, например, 1. Нормированное расстояние между нечетким множеством
между нечетким множеством  и ближайшим к нему обычным множеством называют индексом нечеткости и обозначают
и ближайшим к нему обычным множеством называют индексом нечеткости и обозначают 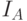 .
.
В таблице 6.3 приведены основные формулы вычисления индекса нечеткости. 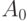 — обычное множество, ближайшее к нечеткому множеству
— обычное множество, ближайшее к нечеткому множеству  ,
, 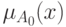 – характеристическая функция множества
– характеристическая функция множества 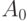 , вычисляемая по формуле (6.7) .
, вычисляемая по формуле (6.7) .
Основные формулы вычисления индексов нечеткости множеств
| Вид метрики | Вид множества | |
 – дискретное множество, – дискретное множество,  число его элементов число его элементов |
![U=[a,b]](/sites/default/files/tex_cache/89743bc7f76b7d334f81d58063ef9a56.png) — непрерывное множество — непрерывное множество |
|
| Линейное расстояние Хемминга | 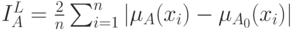 |
 |
| Евклидово расстояние |  |
 |
Пример 6.9
Для множеств  и
и  примера 6.1 рассчитаем в MathCad индексы нечеткости,
примера 6.1 рассчитаем в MathCad индексы нечеткости, 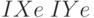 , используя метрику Евклида и
, используя метрику Евклида и  по метрике Хемминга..
по метрике Хемминга..
Индексы нечеткости по Евклиду и по Хеммингу для множеств  и
и  :
:
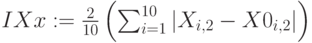 ,
, 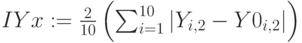
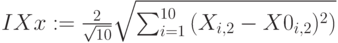 ,
, 

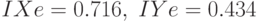
6.7 Экспертные оценки методом нечетких множеств
В процессе принятия решений по вопросам управления организациями достаточно часто прибегают к методу экспертных оценок. Суть метода состоит в следующем: эксперты анализируют проблему, давая количественную оценку характеристикам объектов, в дальнейшем полученные результаты обрабатываются, и на основании анализа мнений группы экспертов принимается решение проблемы.
В такой процедуре возникает, по крайней мере, две проблемы, связанные между собой.
Первая - при оценке объектов эксперты обычно расходятся во мнениях по решаемой проблеме. В связи с этим возникает необходимость оценить степень согласия экспертов количественно. Получение количественной меры согласованности позволяет более обосновано интерпретировать причины расхождений. Вторая - выбор лучшей альтернативы из имеющихся на основе агрегации результатов или, как говорят, свертки с учетом веса мнения эксперта или весомости критерия. Для получения более адекватных оценок в данном анализе можно использовать аппарат теории нечетких множеств. Автором Назаровым Д.М. разработана методика для решения таких задач.
Методика Назарова
Если имеется универсальное множество U, элементы которого имеют неоднозначную составляющую, можно построить нечеткое подмножество  множества
множества  и рассмотреть его характеристическую функцию
и рассмотреть его характеристическую функцию  . Если
. Если  близко к значению 1 или 0, то вклад элемента
близко к значению 1 или 0, то вклад элемента 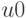 в нечеткость множества
в нечеткость множества  мал. И наоборот, если
мал. И наоборот, если  близко к значению 0,5 (значительно отличается как от 1, так и от 0), то его вклад в нечеткость
близко к значению 0,5 (значительно отличается как от 1, так и от 0), то его вклад в нечеткость  будет значителен. Таким образом, вклад в нечеткость каждого элемента множества определяется близостью или отдаленностью значения функции принадлежности на этом элементе к числам 1 и 0, а мера нечеткости всего множества определяется как сумма вкладов каждого его элемента. Чтобы сравнивать нечеткие множества, имеющие различные носители, надо их нормировать. Представляя имеющиеся данные в виде нормированных нечетких множеств, можно анализировать их с использованием индексов нечеткости. Для вычисления индекса нечеткости
будет значителен. Таким образом, вклад в нечеткость каждого элемента множества определяется близостью или отдаленностью значения функции принадлежности на этом элементе к числам 1 и 0, а мера нечеткости всего множества определяется как сумма вкладов каждого его элемента. Чтобы сравнивать нечеткие множества, имеющие различные носители, надо их нормировать. Представляя имеющиеся данные в виде нормированных нечетких множеств, можно анализировать их с использованием индексов нечеткости. Для вычисления индекса нечеткости 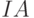 , надо построить ближайшее к нечеткому множество
, надо построить ближайшее к нечеткому множество 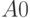 с функцией принадлежности
с функцией принадлежности  (см. 6.6) и рассчитать нормированное расстояние по Хэммингу
(см. 6.6) и рассчитать нормированное расстояние по Хэммингу 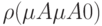 (см. 6.7).
(см. 6.7).
Таким образом, чтобы ответить на вопрос: "Какое из двух множеств "более нечетко"?", надо вычислить и сравнить индексы нечеткости этих множеств. "Более нечетким" является то множество, которое имеет больший индекс нечеткости.
Рассмотрим предложенную методику на примере задачи.
Задача 6.1
Пусть имеются данные экспертных оценок по ряду вопросов. Были поставлены 10 вопросов, 30 экспертов давали оценки по 10- бальной системе. Требуется обработать результаты анкетирования на предмет согласованности оценок. По каким вопросам были даны наиболее согласованные оценки. С другой стороны, какие эксперты были более определенны в своих оценках. Для решения используем методику Назарова.
Постановка задачи
Неоднозначность оценок вызвана с одной стороны, может быть, нечеткой постановкой вопросов, с другой, стороны, у каждого эксперта свое видение проблемы. Учитывая неоднозначность оценок экспертов, будем рассматривать массив данных как множество  , для которого построим нечеткое подмножество
, для которого построим нечеткое подмножество  с характеристической функцией
с характеристической функцией 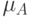 . Проведем анализ нечеткого множества
. Проведем анализ нечеткого множества  по методике Назарова. Для этого рассчитаем индексы нечеткости множеств оценок экспертов и сравним их. При этом, задача распадается на две:
по методике Назарова. Для этого рассчитаем индексы нечеткости множеств оценок экспертов и сравним их. При этом, задача распадается на две:
Задача 6.1.1
Определить индексы нечеткости множеств оценок всех экспертов по каждому вопросу и, тем самым, выявить самые неоднозначные вопросы, при ответе на которые мнения экспертов максимально расходились.
Задача 6.1.2
Определить индексы нечеткости множеств оценок по всем вопросам каждого эксперта и выявить, какой эксперт давал наиболее неоднозначные ответы,
Решение задачи 6.1.1.
Представим решение в системе MathCad. Используем матричное представление данных.
-
Представляем множество оценок
 в виде матрицы
в виде матрицы  . Имеем массив оценок по 10- бальной системе: по 10 вопросам (столбцы) 30 экспертов (строки).
. Имеем массив оценок по 10- бальной системе: по 10 вопросам (столбцы) 30 экспертов (строки). Оценки 30 экспертов:


-
Построим функцию принадлежности
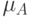 . нечеткого множества оценок
. нечеткого множества оценок  при ответах экспертов на каждый вопрос следующим образом:
при ответах экспертов на каждый вопрос следующим образом:-
Подсчитаем частоту различных оценок при ответе на каждый вопрос:
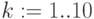
![Z_{j,k}:=\sum_{i=1}^{30}[[(X^{\{j\}}_i)]=k]](/sites/default/files/tex_cache/24525bc3705eca077b182ae254b765b3.png)
Матрица частоты оценок
 :
:
-
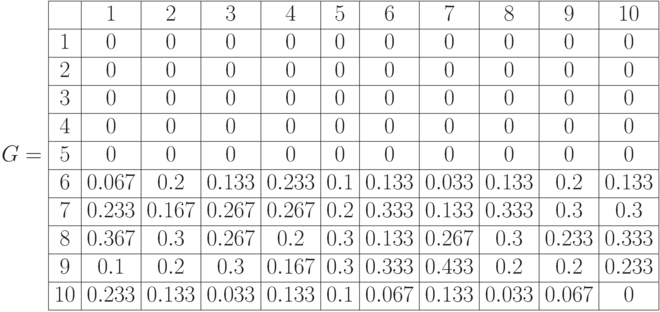
Подсчитаем доли различных оценок при ответе на каждый вопрос. Таким образом, мы выявим степени принадлежности каждой оценки к множеству оценок по рассматриваемому вопросу. Для этого значения каждой ячейки предыдущей таблицы разделим на 30 – по количеству экспертов (Рис.6.14).
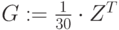
Нечеткое множество экспертных оценок
 :
:
-
Нормируем значения предыдущей таблицы, разделим их на максимальное значение по каждому столбцу. При этом максимальное значение степени принадлежности каждой оценки нечеткому множеству оценок при ответе экспертов на каждый вопрос станет равным единице, и мы получим значения функции принадлежности оценок.
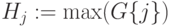
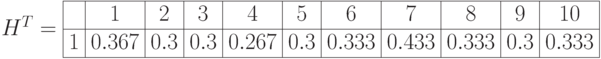

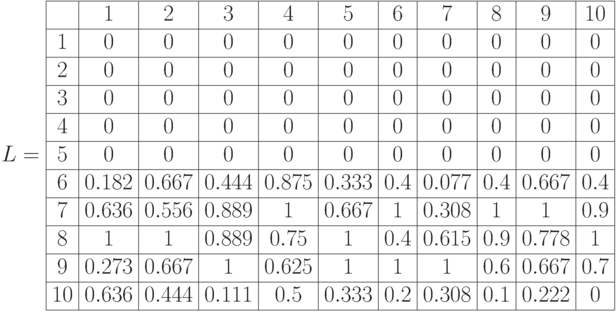
Нормированное нечеткое множество экспертных оценок
 :
:
-
-
Нами получено нечеткое множество оценок экспертов по каждому вопросу
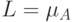 Построим четкое множество, ближайшее к рассматриваемому нечеткому множеству -
Построим четкое множество, ближайшее к рассматриваемому нечеткому множеству - 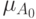 =
= 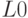 . Применим условную функцию
. Применим условную функцию 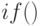 .
.
Множество
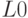 , ближайшее к рассматриваемому нечеткому множеству:
, ближайшее к рассматриваемому нечеткому множеству: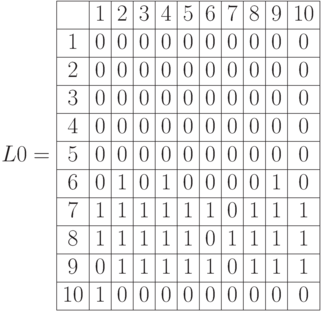
-
Рассчитаем индекс нечеткости по линейной метрике (расстояние по Хэммингу) по формуле :
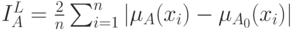 .
.Для этого:
- Вычислим модули отклонений элементов нечеткого множества оценок от ближайшего к нему четкого множества:
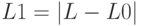
- Найдем суммы по каждому столбцу:

- Транспонируем и рассчитаем индекс нечеткости

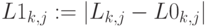 - отклонения – расстрояние по Хэмингу
- отклонения – расстрояние по Хэмингу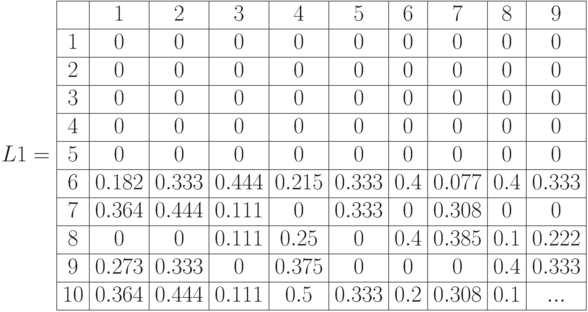
 - сумма по каждому столбцу
- сумма по каждому столбцу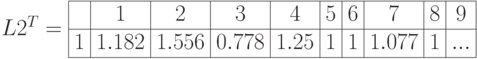
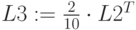 - индексы нечетности
- индексы нечетности
- Вычислим модули отклонений элементов нечеткого множества оценок от ближайшего к нему четкого множества:
-
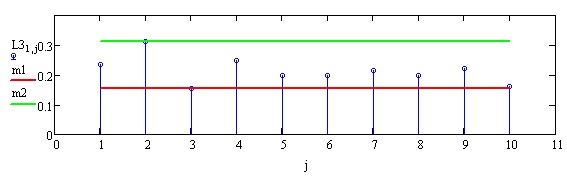
Результат. Построим график и проведем анализ. Для этого сравним индексы нечеткости. Найдем максимальное и минимальное значение индексов нечеткости. Как видно, 2 вопрос вызвал максимальное расхождение в оценках. Возможно, вопрос был поставлен некорректно или невнятно. На 3 вопрос даны наиболее определенные ответы. При этом, следует заметить, что в общем уровень несогласованности для всех вопросов близок.
Анализы ответов на вопросы по индексам нечеткости:

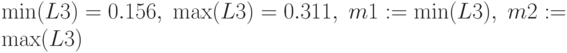
По 2 вопросу наибольшее расхождение, согласованные ответы по 3 вопросу
Решение Задачи 6.1.2
Для исследования нечеткости ответов по всем вопросам каждого эксперта имеем тот же массив оценок, но по 30 экспертам (столбцы), которые давали ответы на 10 вопросов (строки) по 10- бальной системе.
Матрица данных 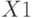 представляет транспонированную матрицу данных
представляет транспонированную матрицу данных  : 30 экспертов отвечают на 10 вопросов
: 30 экспертов отвечают на 10 вопросов

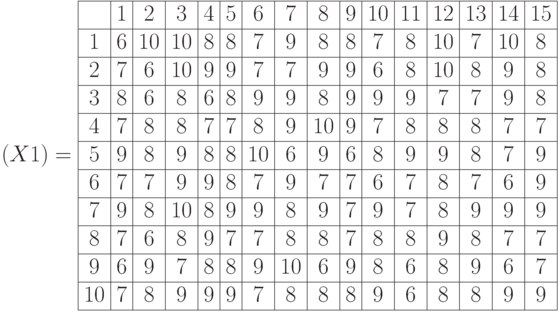
Решение Задачи 6.2.2
Для решения надо выполнить те же действия:
- Используя матрицу данных
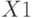 , построить функцию принадлежности
, построить функцию принадлежности 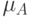 . нечеткого множества
. нечеткого множества  оценок каждого эксперта по всем вопросами.
оценок каждого эксперта по всем вопросами. - Оценить ее по индексам нечеткости
Алгоритм решения тот же самый. Если транспонировать матрицу X1, можно использовать все операторы, но с учетом другого размера матрицы: 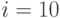 и
и 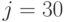 .
.
Результат решения задачи 6.2.2 .
Получены следующие индексы нечеткости.
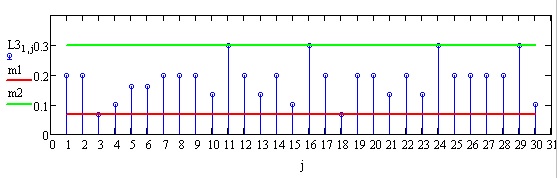
Анализ экспертов по индексам нечеткости
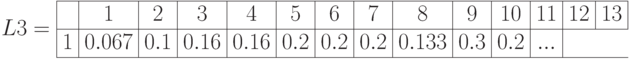
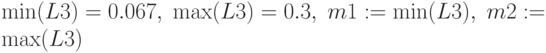
Эксперты 11, 16, 24, 29 дали наиболее размытые оценки.
Эксперты 3 и 18 отвечали наиболее согласованно и определенно.
Как видно, 4 эксперта (11,16,24,29) выделяются наименьшей определенностью своих оценок, два эксперта (3 и 18), напротив, дали согласованные оценки. На этих экспертов можно обратить внимание. На общем уровне согласованность близка.