Нечеткие множества
Прибыль. Ставка дисконтирования.
Аналогичные действия проделаем с показателями  и
и  . Решаем уравнения:
. Решаем уравнения:
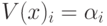 ,
,
где 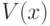 – функция принадлежности, ?i - значение ?-уровня.
– функция принадлежности, ?i - значение ?-уровня.
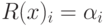 ,
,
где 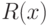 – функция принадлежности,
– функция принадлежности, 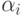 - значение
- значение  -уровня.
-уровня.
Расчеты в Mathcad представлены на Рис. 623б, Рис.6.23в. Получены матрицы  ,
, 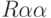 –разложения
–разложения  и
и  по
по  – уровням с значениями
– уровням с значениями 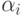 .
.
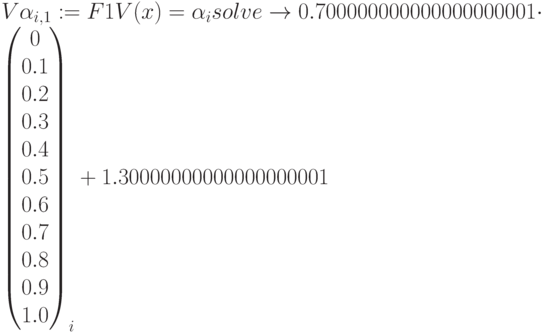


Матрица интервалов достоверности 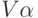 прибыли
прибыли
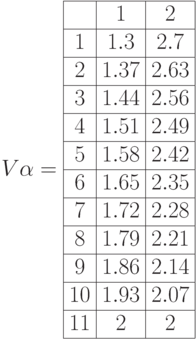
Матрица прибыли  с значениями
с значениями 
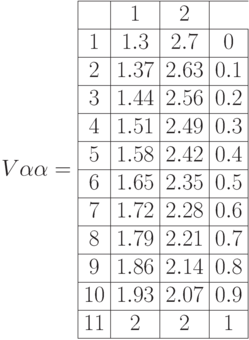
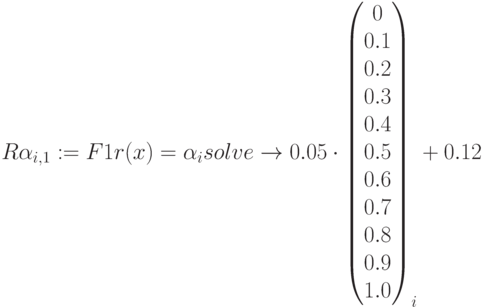
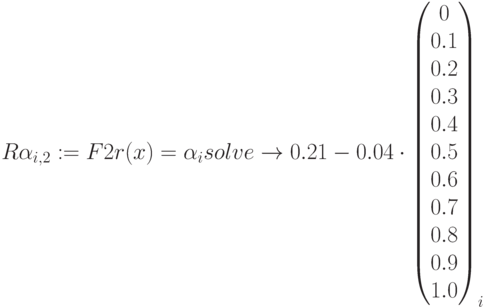

Матрица интервалов достоверности  ставок дисконтирования
ставок дисконтирования
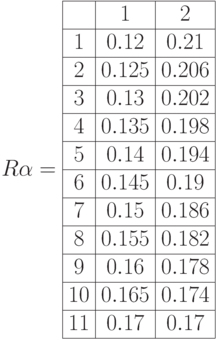
Матрица ставок дисконтирования 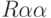 с значениями
с значениями 

Разложение NPV по ?- уровням
Используя матрицы интервалов достоверности 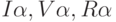 , найдем функцию
, найдем функцию 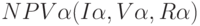 . Представим
. Представим  в виде двух матриц: левый край сечения
в виде двух матриц: левый край сечения 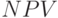 и правый край сечения
и правый край сечения 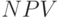 .
.
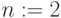
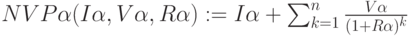

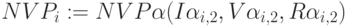
Матрица интервалов достоверности чистой дисконтированной стоимости  (левый край сечения
(левый край сечения  ):
):
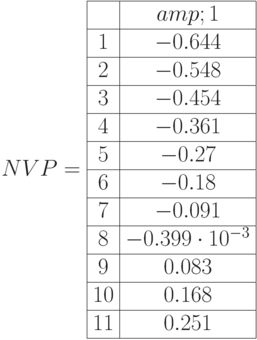
Матрица интервалов достоверности чистой дисконтированной стоимости  (правый край сечения
(правый край сечения  ):
):

 - для левых значений I\alpha, V\alpha, R\alpha, правая часть NPV\alphaR - для правых значений I\alpha, V\alpha, R\alpha. Фактически мы получим функцию принадлежности чистой дисконтированной стоимости
- для левых значений I\alpha, V\alpha, R\alpha, правая часть NPV\alphaR - для правых значений I\alpha, V\alpha, R\alpha. Фактически мы получим функцию принадлежности чистой дисконтированной стоимости  . Функция имеет также треугольный вид и является приближенным разложением нечеткого множества
. Функция имеет также треугольный вид и является приближенным разложением нечеткого множества 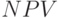 по тем же уровням
по тем же уровням  .
.
Для построения графика треугольной функции принадлежности 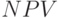 присоединим столбец матрицы
присоединим столбец матрицы  к матрицам
к матрицам 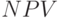 и
и 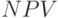 , используя встроенную функцию Mathcad
, используя встроенную функцию Mathcad  . Это будут матрицы
. Это будут матрицы 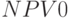 и
и 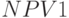 .
.




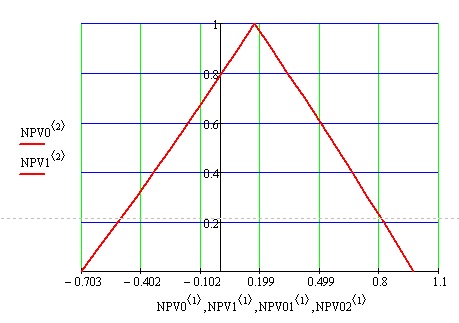
Рис. 6.19. График функции принадлежности нечеткого множества исследуемой чистой дисконтированной стоимости NPV
В результате матрицы 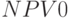 и
и 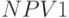 представляют рассчитанные значения
представляют рассчитанные значения 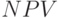 для каждого уровня нечеткости
для каждого уровня нечеткости  , которому соответствуют входные показатели
, которому соответствуют входные показатели 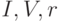 для этого уровня. Значения
для этого уровня. Значения 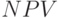 лежат в пределах от -0,707 до 0,976.
лежат в пределах от -0,707 до 0,976.
