Пространство отображения (моделирования) систем

4.1. Системное пространство, его базис и структура.

"Роль топологических понятий в общесистемных абстрактных математических моделях еще не получила в литературе того отражения, которое соответствовало бы важности этих понятий для представления многих основных свойств систем" [104].

Требуется определить пространство, в котором можно было бы отображать (моделировать1^{1В повседневном употреблении <модель>—это нечто похожее на ту вещь, которой она должна соответствовать, но не совсем тождественное ей" [236].}) любую систему. Мы уже использовали, в частном случае, линейное пространство — для отображения времени, и метрическое пространство — для отображения параметров систем. Теперь сформулируем общий подход.

Приведем определение наиболее общего в математике топологического пространства. Вводится множество М, как носитель пространства, на котором задается какая-либо топология (система подмножеств множества М). Для каждой топологии любая система {М}₁ его подмножеств удовлетворяет двум требованиям:

(а) само множество М и пустое множество принадлежит {М}₁;

(б) сумма 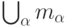любого (конечного или бесконечного) и пересечение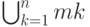

любого конечного числа множеств из {М}₁ принадлежит {М}₁; множества, принадлежащие системе {М}₁, называются открытыми.

Самый прямой способ задать топологию в некотором пространстве состоит в том, чтобы непосредственно указать те множества, которые мы считаем открытыми, или выбрать некоторый базис, или ввести в нем понятие сходимости, или определить в нем операцию замыкания, или задать метрику [101]. Топологическое пространство обозначают как Т=(М,{М}₁). Мы будем рассматривать системное пространство как топологическое при условии возможности указать множество-носитель.

Будем считать, что каждое свойство s_i описывается набором характеристик s_ij, каждая из которых может принимать значения s_ijk. Тогда все проявления свойства s_i можно отображать в подпространстве на индексированном множестве-носителе S_i.

Определим базис (минимальную часть, сохраняющую основные свойства) системного пространства М на наборе множеств S₁, S₂, ..., S₃, ..., S_N, отражающих всевозможные свойства системы, а также множества точек реальное пространство — R и множества моментов времени — T:

(4.1)

Одноименные подпространства будем обозначать теми же буквами, что и множества-носители: 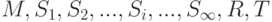. Топологию на М зададим набором характеристик s_ij и наборами их значений s_ijk; R — это трехмерное евклидово пространство, Т — пространство времени, в частном случае линейное. Каждое из пространств S является подпространством пространства М. При этом, в силу диалектического закона перехода количества в качество, подпространства S являются не самостоятельными топологическими пространствами (не удовлетворяется условие (б)), а подпространствами общего топологического пространства M.

Структура каждого из подпространств S_i определяется законами соответствующего свойства и изучается соответствующей частно-научной теорией. Отношения между отдельными подпространствами S_i, а также R и T изучают междисциплинарные теории и некоторые непростые частно-научные теории типа механики (кинематика, динамика), энергетики (теплоэнергетика, электроэнергетика) и т. п. Отношения между S_i, R, T в терминах теории множеств изучают системные теории, а общие отношения между системными свойствами в пространстве и во времени — общая теория систем (ОТС1 и ОТС2).