Состав и структура системного анализа

2.1. Множество разновидностей систем.

Системы, как предмет исследования, образуют совокупность со сложной структурой. Во-первых, все они, в зависимости от класса, могут иметь какую-то мерность. При этом мы не можем утверждать, что это — классы непересекающиеся. Во-вторых, системы могут различаться по роду, стационарности, устойчивости, происхождению, поведению во времени. В-третьих, во внешней среде, базе и самой системе могут присутствовать в той или иной мере другие, неучтенные нами системы. В-четвертых, во внешней среде, базе и в самой системе могут присутствовать, в той или иной мере, свойства других материальных объектов, не относящихся к системам, но и не характеризующих однородную среду. Сами системы мы также отнесли к сложным образованиям, не всегда описываемыми множествами однородных элементов. Таким образом, совокупность всех разновидностей систем, как предмет исследования, не образует множество. Однако, на практике системы всегда могут считаться выделимыми и перечислимыми, поэтому для отображения совокупности всех разновидностей систем мы воспользуемся понятием индексированного множества из булевой алгебры [184].

Под индексированным множеством 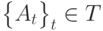мы будем понимать отображение, которое каждому 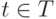ставит в соответствие элемент A_t. Оно не будет отождествляться с множеством всех элементов _At, 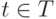. Это существенно, когда необходимо учитывать сложность структуры системы или совокупность разновидностей всех систем. Но во многих случаях это несущественно, например, когда рассматриваются объединения и пересечения систем. Аналогично будем рассматривать многократно индексированные множества, а их отображение — как композицию однократных отображений.

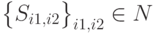Все одномерные системы будем индексировать множеством , где N — числа натурального ряда; двумерные — множеством и т. д. Частичномерные системы будем относить к одномерным.

2.2. Структура системного анализа статических систем.

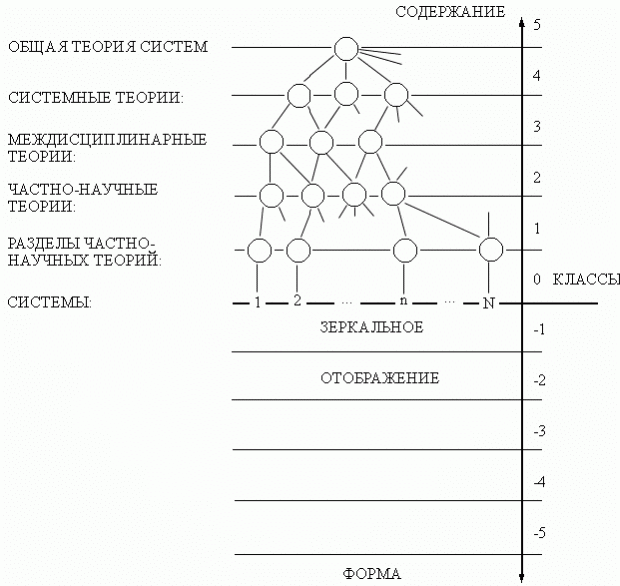
Каждый тип одномерных систем является предметом анализа соответствующих разделов частно-научных теорий (кинематики, динамики, электростатики и т. п.). Двумерные и многомерные системы исследуются частно-научными теориями (механики, экономики и т. д.). Различные классы систем исследуются междисциплинарными теориями (теорией управления, динамических систем, устойчивости, вероятности и др.). Классы систем, где система может быть описана как множество однородных элементов, исследуются системными теориями (множественной, алгебраической, параметрической). Все системы должны исследоваться общей теорией систем. Естественно, что чем большее число типов и классов систем исследует теория, тем более общими понятиями и определениями она должна оперировать.

Рис. 14. Ромбовидная структура системного анализа статических систем

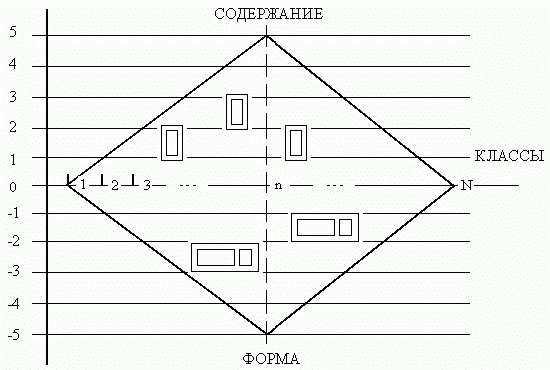
Каждая теория должна располагать средствами исследования систем не только по признаку класса (классов), но и основных уже отмеченных особенностей систем: рода, стационарности, устойчивости, происхождения, типа. Графически структуру индексированного множества разновидностей всех систем и соответствующих теорий исследования можно изобразить ромбовидной схемой (рис. 14).

Количество всех систем — это мощность множества N(N) подмножеств множества N. N — счетнобесконечно. В теории множеств N(N), при N — счетнобесконечном, —континуально.

Каждая теория должна состоять из содержательной части и формального аппарата [224]. Поэтому на схеме указано "зеркальное отображение". Философия считает, что такая "зеркальность" в принципе недостижима [209], т.к. "...даже в высокоразвитых теориях, широко использующих приемы формализованной аксиоматики, кроме формально-аксиоматической части существует некоторый принципиальный неформальный остаток, причем организованный вовсе не по нормам аксиоматико-дедуктивного построения" [198]. На практике такая зеркальность может не наблюдаться: часть содержательных теорий (например, в общественных науках) не имеет формального аппарата, часть — использует аппарат междисциплинарных теорий (например, теорию устойчивости в теории автоматических систем управления), часть — использует аппарат смежных частно-научных теорий (например, теорию цепей в электротехнике). Поэтому ромбовидная структура имеет "дырочно-решетчатый" характер (рис. 15). В ромбовидной структуре заложен двойственный характер формы и содержания системного анализа: "дырки" — "решетки".

Рис. 15. Дырочно-решетчатый вид ромбовидной структуры.

При этом необходимо отметить, что "...именно содержательная теория задает наиболее важные и существенные ориентиры исследования, результаты которого определяются, в первую очередь, не формальными методами, а содержательными теоретическими разработками, осуществленные на предмодельной стадии познания будущего" [115].