Состав и структура системного анализа
2.3. Структура системного анализа динамических систем.
До сих пор мы оперировали статическими понятиями в области систем, явно (d/dt — производная) или неявно (стационарность, устойчивость) подразумевая их зависимость от времени. Однако, поскольку материальные объекты существуют во времени и в пространстве, то определенные нами в пространстве основные понятия системного анализа (система, носитель, база, внешняя среда) зависят также и от времени. Систем, независимых от времени, не существует. Статичность систем является тем условием, которое мы используем для упрощения исследований. При этом под динамической системой мы будем подразумевать
S=S(t), 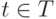 (2.1),
(2.1),
а под статической —
S=S(t)|t=const (2.2),
где t — время.
Из (2.1) и (2.2) следует, что динамическую систему можно отобразить, как последовательность статических:
S(t)=<S(t1), S(t2), ...> (2.3),
где 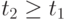 .
.
Возвращаясь к основным понятиям и определениям, отметим, что учет их динамического характера означает:
S=S(t), F=F(t), N=N(t), B=B(t), V=V(t). (2.4).
Аналогично зависимость от времени может быть отражена и для других характеристик и отношений.
В динамическом состоянии систему можно описать, учитывая в (1.14) зависимость от времени:
S(t)=<r(t), SS(t), F(t)>G (2.5),
откуда видно, что реальная (динамическая) система определяется занимаемой частью пространства r(t), совокупностью свойств SS(t), функцией F(t) (в пределах границы G), зависящих от времени.
Возникает естественный вопрос: на каком интервале времени определена F(t) и как зависит состояние системы от ее функции?
ГИПОТЕЗА 4: время существования системы конечно — системы возникают и исчезают.
Эта гипотеза прямо следует из философского принципа конечности любого существования, любая другая альтернатива этой гипотезе не имеет логического ни начала, ни конца. "Любые структуры обладают не бесконечной, а конечной степенью стабильности..." [207]. Время существования системы никогда не бывает бесконечным [33].
* ВРЕМЯ.
Введем время в форме линейного пространства T. Непустое множество T элементов t1, t2, t3,. называется линейным, или векторным пространством, если оно удовлетворяет таким условиям:
— для любых двух элементов 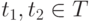 однозначно определен третий элемент
однозначно определен третий элемент  , называемый их суммой и обозначаемый t1+t2, причем
, называемый их суммой и обозначаемый t1+t2, причем
(а) t1+t2=t2+t1 (коммутативность),
(б) t1+(t2+t3)=(t1+t2)+t3 (ассоциативность),
(в) в T существует такой элемент 0, что t1+0=t1 для всех  (существование нуля),
(существование нуля),
(г) для каждого t1 T существует такой элемент (-t1), что t1+(-t1)=0 (существование противоположного элемента);
T существует такой элемент (-t1), что t1+(-t1)=0 (существование противоположного элемента);
— для любого числа a и любого элемента 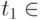 T определен элемент
T определен элемент  (произведение элемента t1 на число a), причем
(произведение элемента t1 на число a), причем
(д) 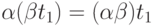 , где
, где 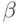 — тоже число,
— тоже число,
(е) 1t1=t1,
(ж) 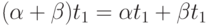 ,
,
(з) 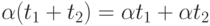 ,
,
где t1, t2, ..., ti, ... — моменты времени, 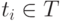 .
.
Время однонаправлено, т.е. возможны только последовательности типа ti-1 , ti, ti+1, ..., где tiiti-1.
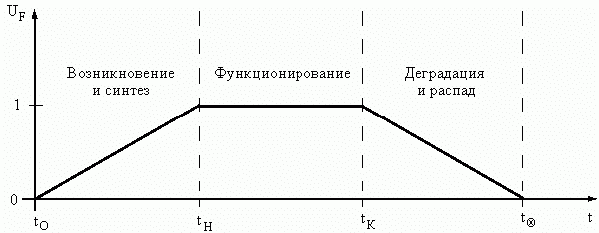
Из гипотезы 4 следует, что система существует на конечном отрезке времени [tH, tK], где tH<tK. Поскольку все системы реальны ("совокупность свойств"), а значит и инерционны, то переход от несистемы (в момент t0) к системе (tH) и, наоборот, от системы (tK) к несистеме (tД) осуществляется за конечный интервал времени, т.е. t0<tН<tК<tД.
Введем следующие понятия и определения:
— момент возникновения системы — t0,
— отрезок времени синтеза системы — [t0, tH],
— отрезок времени функционирования системы — [tH, tK],
— отрезок времени деградации системы — [tK, 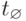 ],
],
— момент распада системы — 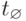 .
.
Указанные моменты и отрезки времени определяют стадии простой эволюции или периоды жизни системы [55].Оценивая развитость системы по уровню организации ее функции UF (см. (1.19)), простую эволюцию системы можно представить, как показано на рис. 15а.
Существование множества разновидностей систем определяет возможность превращения систем. Биология и системотехника используют понятие "эволюция систем", подразумевая под ним ряд живых или искусственных систем, в котором каждая пара соседних систем одинаково идентифицируется в классификации систем, но имеет различия в составляющих: в занимаемой части пространства r(t) или в свойствах SS(t), при одинаковой функции F(t). Для учета таких превращений систем введем понятие "циклическая эволюция системы".
Таким образом, мы имеем следующие основные стадии существования систем: I — возникновение и синтез, II — устойчивое, стационарное функционирование, III — деградация и распад, IV — циклическая эволюция.
Системный анализ, как наука о системах, должен располагать средствами исследования систем на любой стадии. Структуру системного анализа, учитывающего стадии (динамику) систем, графически изобразим в форме "дискретной, зеркальной пирамиды" (рис. 16).
Естественно, что системный анализ динамических систем также может не располагать средствами для исследования всех классов систем на всех стадиях. Этот факт можно изобразить в виде "дырочно-решетчатой" пирамидальной структуры. При этом "дырки" и "решетки" одного ромба могут не совпадать с "дырками" и "решетками" другого ромба.
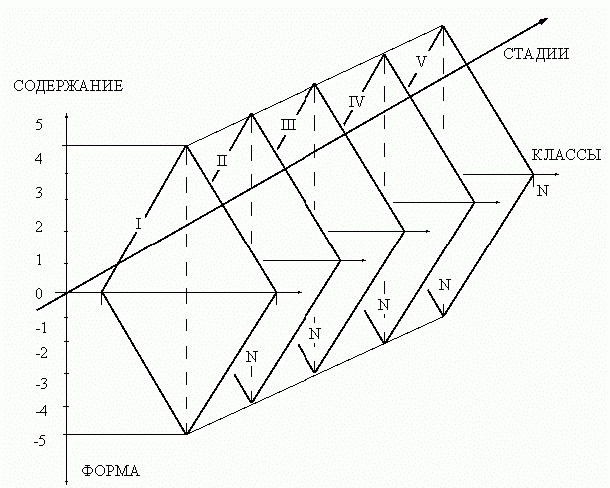
Рис. 16. Пирамидальная структура системного анализа динамических систем. Дополнительные к рис. 15 обозначения: 0 — статические системы, I — возникновение и синтез, II — устойчивое, стационарное функционирование, III — деградация и распад, IV — циклическая эволюция.
Это означает, что какая-то теория располагает средствами исследования одной стадии заданного класса систем и не располагает средствами исследования того же класса систем, но находящихся в другой стадии. Например, теория проектирования не исследует эволюцию, теория прогнозирования не исследует функционирование систем и т. п.
Введем метрическое, т.е. нормальное и имеющее счетную базу, пространство.
Метрическим пространством называется пара 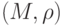 , состоящая из некоторого множества (пространства) M элементов (точек) и расстояния, т.е. однозначной, неотрицательной, действительной функции
, состоящая из некоторого множества (пространства) M элементов (точек) и расстояния, т.е. однозначной, неотрицательной, действительной функции 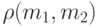 , определенной для любых m1 и m2 из M и подчиненной следующим трем аксиомам:
, определенной для любых m1 и m2 из M и подчиненной следующим трем аксиомам:
(а) 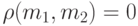 тогда и только тогда, когда m1=m2,
тогда и только тогда, когда m1=m2,
Само метрическое пространство, т.е. пару 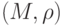 , мы будем обозначать, как правило, одной буквой:
, мы будем обозначать, как правило, одной буквой:
R=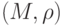 .
.
* ЧАСТНЫЙ СЛУЧАЙ.
В случае, когда систему (2.5) удается описать множеством параметров Q1, Q2, ..., Qn в метрическом пространстве R (в пространстве состояний системы), изменяемых непрерывно во времени и дифференцируемых, а внешние отношения (1.15) свести к одному входному (x(t)) и одному выходному (y(t)) векторам, тогда изучение изменения системы во времени можно осуществлять с помощью методов и средств классической теории динамических систем [75]. Система описывается функцией F(t) и отношениями с внешней средой и отображается динамикой параметров и характеристик. Задача решается в два этапа.
На первом этапе систему отображают через множество параметров, называемых переменными состояния. Аналитически их изменение выражается множеством n одновременно дифференцируемых уравнений первого порядка:
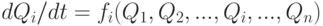 .
.
Эти уравнения называются динамическими, или уравнениями движения. Производные более высокого порядка не учитываются. Множество дифференциальных уравнений позволяет формально выражать такие системные свойства, как целостность, устойчивость, эволюция. Геометрически изменение системы выражается траекториями переменных состояния в n-мерном пространстве. Независимое от времени состояние
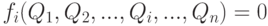
может быть рассчитано как точка в пространстве R, т.е. стационарное состояние системы.
На втором этапе исследуются отношения системы с внешней средой. Однонаправленные, детектируемые отношения с внешней средой, называемые "входами" и "выходами" системы, можно отобразить системой линейных дифференциальных уравнений

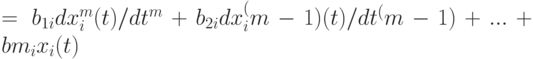 ,
,
где i = 1, 2, ... — "входы" и "выходы" системы; b1, b2, ..., bm — параметры "входа"; a1, a2, ..., an — параметры "выхода".
"Линейная модель в достаточной степени допустима для описания поведения динамической системы в устойчивом, стационарном состоянии" [27].

 (
(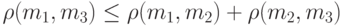 (
(