Статический анализ систем

6.1. Теория статического анализа систем.

Мы не считаем всю область системного анализа подчиняющейся только дедуктивной ОТС. Помимо дедуктивных аксиом в этой области могут иметь место индуктивные принципы, аналитико-синтетические положения, гипотезы и т. п. Конечно, такой набор средств может приводить к противоречию двух выражений одного и того же высказывания.

Все сказанное относится и к теории статического анализа систем (теории САС). Поэтому теорию САС мы будем развивать на базе ОТС, параллельно используя и другие средства.

В теории статического анализа, как в одном из разделов системного анализа, должны действовать все понятия, аксиомы и правила вывода ОТС.

Определим предметом исследования теории САС статические (несвязанные со временем) состояния систем (см. рис. 14). Статические состояния системы отражаются состояниями составных частей системы, базы и внешней среды (см. рис. 10) и их внешних (1.9 — 1.12) и внутренних (1.20 — 1.23) структур. Наша задача состоит в детализации частей системы, базы и внешней среды, их внешних и внутренних структур. Для отображения систем будем использовать системное пространство (§4.1).

Пусть на системообразующем свойстве s_i материального объекта N со свойствами s_N образована система S с функцией F, базой B, внешней средой V и границей с внешней средой G. Реальное пространство — R, его свойства — 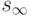, время — Т, материя — .

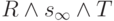ГИПОТЕЗА 5. Ограничение материального объекта некоторой границей ограничивает число свойств, которыми может обладать этот объект [24, с. 21]. В частности, число свойств объекта может быть конечно.

Пусть выбранный материальный объект обладает набором s_N свойств. Тогда, в соответствии с ОТС (см. табл. 8), имеем:

,

,

,

,

,

,

,

.

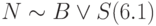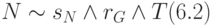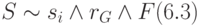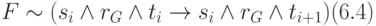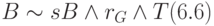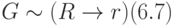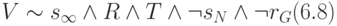Внешние отношения, порождающие функцию системы:

.

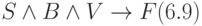По условию статичности из рассмотрения исключается время и исследованию подлежат свойства и их размещение в пространстве:

,

,

,

,

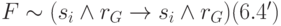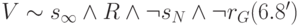а также 6.1, 6.3, 6.5, 6.7, 6.9, т. е. статический анализ сводится к исследованию структур свойств и пространственных структур.

Система в статике (6.3) — это совмещение структуры системообразующих свойств s_i, пространственной структуры r_G и функциональной структуры F. При этом F порождается выделением системы из внешней среды и базы (6.9), а ее структура определяется структурами s_i и r_G. Для одной и той же F могут существовать различные s_i и r_G, удовлетворяющие (6.3).

СЛЕДСТВИЕ 1. Всякая функция системы может быть реализована на некотором множестве структур системообразующих свойства и пространственных структур.

СЛЕДСТВИЕ 2. Всякая система характеризуется функциональной структурой, структурой системообразующих свойств и пространственной структурой.

Пространственная структура — это часть евклидова пространства R, занимаемая материальным объектом-носителем.

Структура системообразующих свойств s_i — это часть подпространства S_i топологического пространства 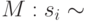<s_ij, s_ijk>.

Для отображения функциональных структур у нас средства отсутствуют. Поэтому отметим, что функция F системы фактически является новым целостным свойством, которое приобретает материальный объект-носитель.

СЛЕДСТВИЕ 3. Образование системы является формой приобретения материальным объектом новых целостных свойств.

С учетом СЛЕДСТВИЯ 3 мы можем в топологическом пространстве М считать одно из подпространств S функциональным, но, чтобы выделить его, будем это подпространство обозначать как F , а для определения М будем вместо (4.1) использовать формулу

.

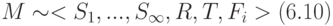База системы в статике (6.6') — это структура ее свойств sB и пространственная структура r_G, отображаемых в подпространствах: состояний SB и евклидовом R, соответственно. При этом, в соответствии с ГИПОТЕЗОЙ 5, число свойств базы конечно.

Внешняя среда в статике (6.8') — это структура ее свойств и пространственная структура . Поскольку 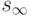и R бесконечны, то структура свойств — это практически структура 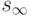, а пространственная структура — это практически все реальное пространство R. Их отображение осуществляется в 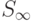и R, соответственно. Из-за бесконечности 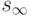и R, на практике их ограничивают наиболее существенными отношениями системы и базы с внешней средой (см. (6.9), а также (1.9) — (1.12)).

Дальнейшая детализация теории статического анализа систем должна осуществляться, в соответствии с классификационными схемами (рис. 13), путем выделения особенностей структур отдельных классов, родов, видов и типов систем. При этом, с учетом статичности состояния, все системы считаются стационарными и устойчивыми. Такими исследованиями занимается теория структур [125, 139], частно-научные [26], междисциплинарные и системные теории. Математическая теория структур [21] носит пока, к сожалению, слишком абстрактный характер.