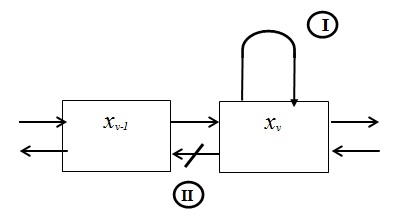
Рынок как система с явными потерями
3.2. Дифференциальные уравнения Эрланга
Введём понятия макросостояния группы потребителей. Сообщество из  групп потребителей может иметь одно микросостояние из набора
групп потребителей может иметь одно микросостояние из набора  состояний:
состояний:
 - свободны все группы потребителей;
- свободны все группы потребителей;
 - занята ровно одна группа потребителей ;
- занята ровно одна группа потребителей ;
…
 - занято ровно
- занято ровно  групп потребителей;
групп потребителей;
…
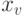 - заняты все
- заняты все  потребителей
потребителей
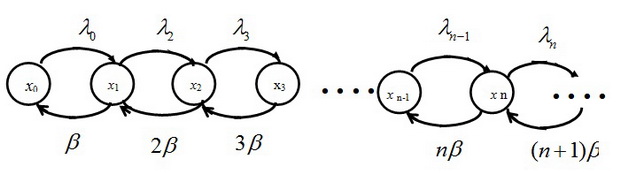
Диаграмма состояний и переходов показана на рисунке 3.3:
Вероятность того, что система в момент времени  находится в состоянии
находится в состоянии  обозначим
обозначим 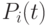 ;
; 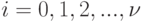 .
.
Так как все возможные состояния представляют собой полную группу
событий, то для любого момента  :
:

I. Запишем дифференциальное уравнение для 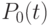 .
.
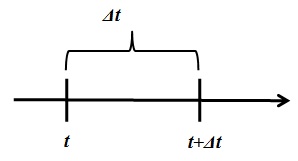
Рассмотрим отрезок (рис. 3.3) времени 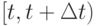 :
:
 - вероятность того, что за время
- вероятность того, что за время  поступит партия товаров;
поступит партия товаров;
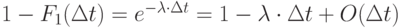 - вероятность того, что за время
- вероятность того, что за время  партия товаров не поступит;
партия товаров не поступит;
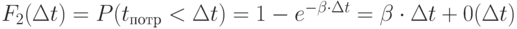 - вероятность того, что за время
- вероятность того, что за время  группа потребителей освободится;
группа потребителей освободится;
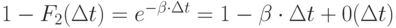 - вероятность того, что за время
- вероятность того, что за время  группа потребителей не освободится.
группа потребителей не освободится.
Найдём вероятность того, что в момент 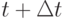 система будет находиться
система будет находиться
в состоянии  ( все группы потребителей свободны) -
( все группы потребителей свободны) -
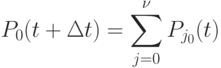 |
( 3.3) |
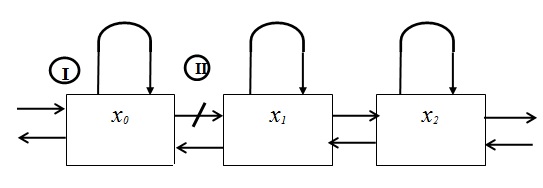
Это может произойти двумя способами (число стрелок в  - две):
- две):
Первый вариант (I) - в момент  система находилась в состоянии
система находилась в состоянии  , и за время
, и за время  не поступило ни одного вызова (система не перешла в состояние
не поступило ни одного вызова (система не перешла в состояние  );
);
Bторой вариант (II) - в момент  система находилась в состоянии
система находилась в состоянии  , и за время
, и за время  группа потребителей освободилась, и система перешла в состояние
группа потребителей освободилась, и система перешла в состояние  (рис. 3.5) .
(рис. 3.5) .
Возможностью перехода рынка из  в
в  (одновременно освободилось две группы потребителей) при малом
(одновременно освободилось две группы потребителей) при малом  можно пренебречь, так как поток
можно пренебречь, так как поток
освобождений ординарный, то есть

По теореме сложения вероятностей:
 |
( 3.4) |
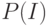 найдём по теореме умножения. Вероятность того, что в момент
найдём по теореме умножения. Вероятность того, что в момент  рынок был в состоянии
рынок был в состоянии  , равна
, равна 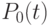 . Вероятность того, что за время
. Вероятность того, что за время  не придёт ни одной партии товара, равна
не придёт ни одной партии товара, равна  .
.
Так как  , отсюда:
, отсюда:
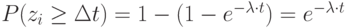
Вспомним ряд Маклорена - 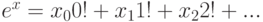 .
.
С точностью до величины высшего порядка малости -  .
.
Следовательно, 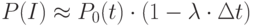 .
.
Найдём 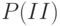 . Вероятность того, что в момент
. Вероятность того, что в момент  система была в состоянии
система была в состоянии 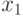 , равна
, равна 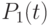 . Вероятность того, что за время
. Вероятность того, что за время  одна линия освободится, равна
одна линия освободится, равна 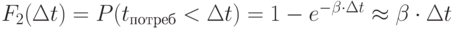 .
.
С точностью до бесконечно малых более высокого порядка малости,
чем  :
: 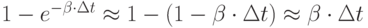
Следовательно, 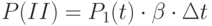 .
.
Подставляя вместо 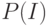 и
и 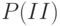 их значения, получим:
их значения, получим:
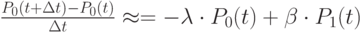
Переходя к пределу при 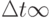 , получим:
, получим:
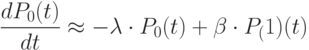 |
( 3.5) |
Аналогичные дифференциальные уравнения составим и для других
вероятностей состояний.
I.Возьмём любое 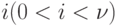 и найдём вероятность
и найдём вероятность 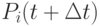 того, что в момент
того, что в момент 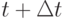 система будет в состоянии
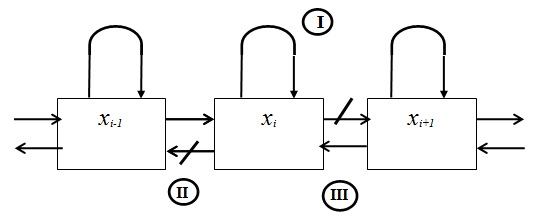
система будет в состоянии  (рис. 3.6)
(рис. 3.6)
Вообще  .
.
Эта вероятность вычисляется как вероятность суммы трёх событий (по числу стрелок, направленных в  ):
):
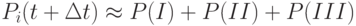
Событие  - в момент t рынок был в состоянии
- в момент t рынок был в состоянии  , а за время
, а за время  не
не
перешла из него ни в 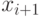 , ни в
, ни в 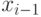 (ни одна партия товара не поступила и ни одна из
(ни одна партия товара не поступила и ни одна из  групп потребителей не освободилась);
групп потребителей не освободилась);
Событие I - в момент
- в момент  рынок был в состоянии
рынок был в состоянии 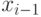 (заняты
(заняты 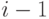 группа потребителей), а за время
группа потребителей), а за время  перешёл в состояние
перешёл в состояние  (поступил одна группа товаров);
(поступил одна группа товаров);
 - в момент
- в момент  рынок был в состоянии
рынок был в состоянии  (занята
(занята  группа потребителей)
группа потребителей)
а за время  одна группа потребителей освободилась.
одна группа потребителей освободилась.
То есть 
Найдём P (I) . Вероятность того, что за время  не поступит ни одной партии товаров и не освободится ни одна группа потребителей, равна:
не поступит ни одной партии товаров и не освободится ни одна группа потребителей, равна:
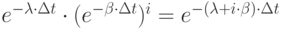 ,
,
где 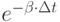 - вероятность того, что не освободятся группы потребителей с первой по
- вероятность того, что не освободятся группы потребителей с первой по  -ю.
-ю.
Пренебрегая малыми величинами высших порядков, имеем:
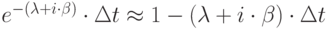
Таким образом: ![P(I)=P_i (t)\cdot [1-(\lambda+i\cdot \beta)\cdot \Delta t]](/sites/default/files/tex_cache/2dfac1dd3793416b028beb396ec2d5f0.png)
Найдём 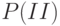 . Вероятность поступления одного одной партии товара за
. Вероятность поступления одного одной партии товара за  равна:
равна:
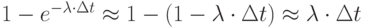
Следовательно:

Найдём 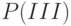 . Вероятность освобождения за время
. Вероятность освобождения за время  одной из
одной из  занятых групп потребителей (или первая, или вторая, … или
занятых групп потребителей (или первая, или вторая, … или  -я):
-я):
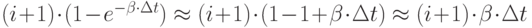
Следовательно:
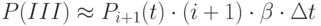
Подставляя значения 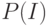 ,
, 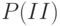 и
и 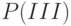 , получим:
, получим:
![P_i (t+\Delta t)=P_i (t)\cdot [1-(\lambda +i\cdot \beta)\cdot \Delta t]+P_{i-1}(t)\cdot \lambda \cdot \Delta t+P_{i+1}(t)\cdot (i+1)\cdot \beta \cdot \Delta t](/sites/default/files/tex_cache/34d894143ce6ac16c8a60d5320fc2821.png)
Перенесём 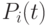 в левую часть, разделим на
в левую часть, разделим на  и, переходя к пределу, получим дифференциальное уравнение для
и, переходя к пределу, получим дифференциальное уравнение для 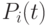 при
при 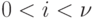 :
:
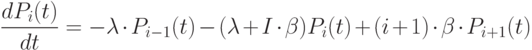 |
( 3.6) |
III. Составим уравнение для последней вероятности 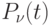 - это вероятность того, что все
- это вероятность того, что все 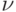 групп потребителей будут заняты (рис. 3.7).
групп потребителей будут заняты (рис. 3.7).
Это может произойти двумя способами:
I - в момент времени  рынок находился в состоянии
рынок находился в состоянии 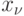 и за время
и за время  ни одна группа потребителей не освободилась. Вероятность того, что за время
ни одна группа потребителей не освободилась. Вероятность того, что за время  не освободится первая группа потребителей, равна
не освободится первая группа потребителей, равна 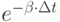 . Вероятность того, что не освободится и первая, и вторая, … , и
. Вероятность того, что не освободится и первая, и вторая, … , и 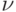 -я группа потребителей равна:
-я группа потребителей равна:
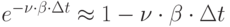 . Тогда
. Тогда 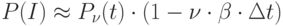 ;
;
II - в момент времени  система находилась в состоянии
система находилась в состоянии 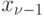 и за время
и за время  произошло занятие одной группы потребителей. Вероятность поступления одного партии товаров за
произошло занятие одной группы потребителей. Вероятность поступления одного партии товаров за  равна
равна 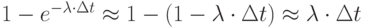 .
.
Тогда 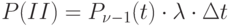 .
.
Вероятность того, что в момент 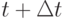 система будет находиться в состоянии
система будет находиться в состоянии 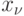 :
:
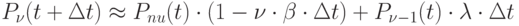

Таким образом, получена система дифференциальных уравнений для вероятностей 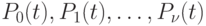
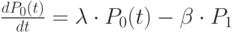 …
…
![[[dP] \downarrow \nu (t_))/dt=\lambda \cdot P_{\downarrow }i(t)-[(\lambda + I \cdot \beta) \cdot P]_{ \downarrow }i(t)+[(i+1)\cdot \beta )\cdot P]_{ \downarrow }(i+1)_{(t)}](/sites/default/files/tex_cache/74a939a89020893d1e3b829e707ca249.png) …
…
 |
( 3.7) |
Эти уравнения называются дифференциальными уравнениями Эрланга.
Эти уравнения описывают так называемый процесс рождения и гибели.
Прежде чем перейти к решению системы Эрланга, рассмотрим
закономерности изменения 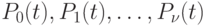 .
.