Позиционные системы счисления. Представление целых чисел

Формальный алгоритм перевода десятичного числа в систему с основанием p

Алгоритм достаточно прост. На пальцах он выглядит так. Необходимо последовательно делить число на p - основание системы счисления. Остатки от деления дают цифры для записи числа в системе с основанием p.

Приведу обоснование алгоритма:

Воспользуемся представлением (*) для записи числа N.

1. Положим ;
2. Представим число M в виде:
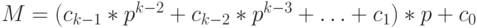
3. Нетрудно видеть: 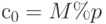, где операция % означает остаток от деления;
4. Вычислим новое значение 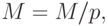где операция / означает деление нацело. Результатом этой операции является число, от которого отрезана последняя цифра; Полученное число сохраняет представление (*).
5. Операции 3 и 4 будем повторять раз, получая каждый раз очередную цифру в разложении по степеням основания .

Вот как выглядит точная запись этого алгоритма в виде функции на языке С#:

  /// <summary>
    /// Перевод десятичного числа N 
    /// в систему счисления с основанием p
    /// </summary>
    /// <param name="N"> переводимое число</param>
    /// <param name="p">основание системы счисления</param>
    /// <returns>
    /// строка, задающая запись числа 
    /// в системе с основанием p
    /// </returns>
    static string Perevod10ToP(int N, int p)
    {
      string result = "";
      int M = N;
      while (M != 0)
      {
        result = (M % p).ToString() + result;
        M = M / p;
      }
      return result;
    }
    

К этому алгоритму мы еще вернемся, а сейчас рассмотрим несколько менее тривиальных задач, на тему представления чисел в системах счисления.

Задача 5: Число 77 в системе счисления с основанием p заканчивается на 0, а число 29 в этой системе заканчивается на 1. Чему равно p – основание системы счисления?

Ответ: 7

Решение: При обосновании алгоритма перевода было показано, что с учетом представления (*) любое число может быть записано в виде:

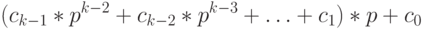
Отсюда следует возможность представить наши числа 77 и 29 следующим образом:

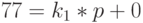
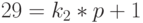
Следовательно, справедливо соотношение:

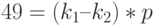
Произведение двух целых, отличных от 1, равно 49 в том и только в том случае, когда:

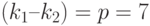
Задача 6: Двузначное число N в системах счисления с основаниями 3 и 7 заканчивается одной и той же цифрой. Укажите минимально возможное значение N.

Ответ: 21

Решение: N представимо в виде:

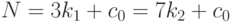
Следовательно, справедливо соотношение:

Минимальное значение для N получается при:

Алгоритм перевода десятичных чисел в систему счисления с основанием p следует хорошо знать. В ряде задач он используется для разбора десятичного числа на цифры. Зная число цифр в числе, их сумму или произведение, можно найти минимальное, максимальное или все числа, удовлетворяющие заданным характеристикам. Вот несколько задач на эту тему:

Задача 7:

При выполнении фрагмента программы на печать выводятся два числа - 3 и 18.

Каким может быть минимальное (максимальное) значение числа в этом случае?

  int a = 0, b = 0;
  while (N != 0)
  {
    a = a + 1;  //число цифр в числе
    b = b + N % 10;  //сумма цифр
    N = N / 10;
  }
  Console.WriteLine(" a = " + a.ToString());
  Console.WriteLine(" b = " + b.ToString());
    

Ответ: минимальное 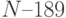; максимальное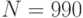

Решение: Если в качестве основания системы использовать число 10, то алгоритм позволяет разобрать десятичное число на цифры. Переменная a играет роль счетчика цикла, задавая тем самым число цифр в числе. Переменная в данном фрагменте вычисляет сумму цифр. Задача сводится к определению к-значного числа по заданной сумме его цифр. Если сумма трех цифр числа равна 18, то первой цифрой у числа с минимальным значением может быть цифра 1. Две оставшиеся цифры в сумме дают 17, откуда и следует ответ. Для максимального числа, последней цифрой может быть 0, а две старшие цифры могут быть равны 9.

Задача 8:

При выполнении фрагмента программы на печать выводятся два числа - 3 и 18.

Перечислите все возможные значения числа в этом случае?

  int a = 0, b = 1;
  while (N != 0)
  {
    a = a + 1;  //число цифр в числе
    b = b * N % 10;  //произведение цифр
    N = N / 10;
  }
  Console.WriteLine(" a = " + a.ToString());
  Console.WriteLine(" b = " + b.ToString());
    

Ответ: (129, 136, 163, 192, 219, 233, 291, 316, 323, 332, 361, 613, 631, 912, 921)

Решение: Эта задача является вариацией предыдущей задачи. Здесь необходимо определить возможное значение трехзначного числа, зная произведение его цифр. В ответе перечислены все возможные решения.