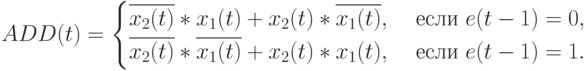Базовые положения теории многофункциональных логических модулей
С практических позиций достаточно рассмотреть схемотехнические особенности использования PD- ассоциативные конструкций при реализации следующих бит-операций [130]:
- "арифметическая сумма" (ADD),
- "запоминание единицей" (ST1),
- "неравнозначность" (XOR),
- "логическое умножение"(AND),
- "логическое умножение с инверсией"(NAND).
Все перечисленные бит-инструкции реализуются в бит-процессоре с принудительной задержкой на 1 такт, за исключением операции ST 1, в которой принудительная задержка составляет 2 такта.
Согласно таблице истинности (табл. 5.7) потоковую бит-операцию ADD можно представить в PD- ассоциативном виде:
где целочисленное время  изменяется от
изменяется от  до
до 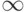 .
.
В (5.30) PD- ассоциативная и в данном случае переключательная конструкция проявляется в том, что в зависимости от содержимого "единицы переноса" на предыдущем такте 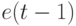 :
:
- "единица переноса" на текущем такте
 реализуется либо как бит-операция
реализуется либо как бит-операция 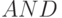 , либо как бит-операция
, либо как бит-операция 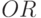 ;
; - "арифметическая сумма" на текущем такте
 реализуется либо как
реализуется либо как  , либо как
, либо как  .
.
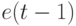 |
 |
 |
 |
 |
|---|---|---|---|---|
| 0 | 0 | 0 | 0 | 0 |
| 0 | 0 | 1 | 1 | 0 |
| 0 | 1 | 0 | 1 | 0 |
| 0 | 1 | 1 | 0 | 1 |
| 1 | 0 | 0 | 1 | 0 |
| 1 | 0 | 1 | 0 | 1 |
| 1 | 1 | 0 | 0 | 1 |
| 1 | 1 | 1 | 1 | 1 |
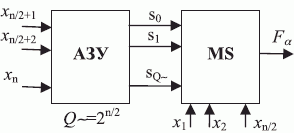
В логической схеме (рис. 5.12), реализующей PD- ассоциативную конструкцию (5.30), "единица переноса" 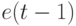 является промежуточной переменной и подается на
является промежуточной переменной и подается на 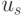 -входы селектора-мультиплексора, формируя на них управляющий вектор
-входы селектора-мультиплексора, формируя на них управляющий вектор
 |
( t-1))) |
В данном случае PD- ассоциативная конструкция реализуется на селекторе-мультиплексоре с четырьмя коммутируемыми входами  ), который в тоже время является универсальным логическим модулем по отношению к двум переменным
), который в тоже время является универсальным логическим модулем по отношению к двум переменным 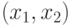 , причем управляющая ассоциативная переменная
, причем управляющая ассоциативная переменная 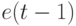 является внутренней и недоступна пользователю.
является внутренней и недоступна пользователю.
Согласно таблице истинности (табл. 5.8) потоковую бит-операцию 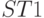 можно представить в PD- ассоциативном виде:
можно представить в PD- ассоциативном виде:
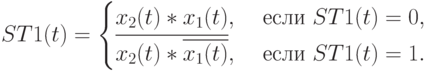 |
( 5.31) |
 |
 |
 |
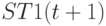 |
|---|---|---|---|
| 0 | 0 | 0 | 0 |
| 0 | 0 | 1 | 0 |
| 0 | 1 | 0 | 0 |
| 0 | 1 | 1 | 1 |
| 1 | 0 | 0 | 1 |
| 1 | 0 | 1 | 1 |
| 1 | 1 | 0 | 0 |
| 1 | 1 | 1 | 1 |
В словесном виде (5.31) выражается: на выход канала АЛУ поступает переменная  , если
, если  , а при
, а при  на выходе сохраняется последнее значение
на выходе сохраняется последнее значение 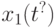 , отвечающее
, отвечающее  , что дает эквивалентную форму записи:
, что дает эквивалентную форму записи:
 |
( 5.32) |
где 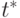 - последний предшествующий момент времени, когда
- последний предшествующий момент времени, когда  .
.
В данном случае PD- ассоциативная конструкция также является переключательной и в зависимости:
- от собственного значения
 , которое в (5.31) является не только выходной, но и внутренней переменной, реализуется либо как
, которое в (5.31) является не только выходной, но и внутренней переменной, реализуется либо как 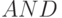 , либо как
, либо как 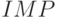 (импликация:
(импликация:  );
); - от значения внешней переменной
 , которое в записи (5.32) переводит канал АЛУ бит-процессора из режима транзитной передачи переменной
, которое в записи (5.32) переводит канал АЛУ бит-процессора из режима транзитной передачи переменной  (при
(при  ) в режим запоминания последнего прошедшего на выход значения
) в режим запоминания последнего прошедшего на выход значения  (при
(при  ).
).
При выполнении потоковой бит-операции 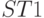 (рис. 5.13) управляющий вектор
(рис. 5.13) управляющий вектор  формируется как за счет ассоциативных
формируется как за счет ассоциативных  , так и не ассоциативных переменных
, так и не ассоциативных переменных  , причем первые могут быть как внутренними (задаваемыми фиксированной схемой соединения вентилей) и недоступными пользователю
, причем первые могут быть как внутренними (задаваемыми фиксированной схемой соединения вентилей) и недоступными пользователю 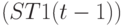 , так и внешними (
, так и внешними (  ) и доступными пользователю.
) и доступными пользователю.
Именно эквивалентность форм записи (5.31) и (5.32) объективно подтверждает существование в вычислительной технике дуализма между потоками инструкций и данных, т. к. в записи (5.31)  считается информационной переменной, а
считается информационной переменной, а  - управляющей, в то время как в записи (5.32) они меняются ролями.
- управляющей, в то время как в записи (5.32) они меняются ролями.
Из приведенных данных видно:
- Ассоциативное "замыкание" бит-операнда
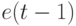 на поток бит-инструкций позволило реализовать ЛФ трех переменных
на поток бит-инструкций позволило реализовать ЛФ трех переменных 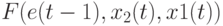 на двухвходовом УДМ2.
на двухвходовом УДМ2. - Разложение Стоуна - Шеннона произвольной
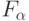 типа (5.13)
типа (5.13)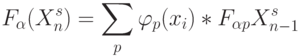
допускает ассоциативное замыкание любой переменной
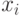 на соответствующее
на соответствующее 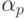 -подмножество функций с входным вектором размерности
-подмножество функций с входным вектором размерности 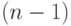 . Здесь
. Здесь  - характеристическая функция:
- характеристическая функция:
- Для ассоциативного "замыкания" можно использовать не только входные, но и выходные и "внутренние" переменные, причем в последних двух случаях речь уже идет о конечных, а не комбинационных автоматах.
- Если продолжить разложение Стоуна - Шеннона для функций
 и т. д., то окажется, что для ассоциативного замыкания можно использовать составной вектор, компоненты которого представляют собой произвольную комбинацию подмножеств входных, внутренних и выходных переменных.
и т. д., то окажется, что для ассоциативного замыкания можно использовать составной вектор, компоненты которого представляют собой произвольную комбинацию подмножеств входных, внутренних и выходных переменных.
В частности, в классе булевых функций ассоциативная схема УДМn приобретает вид рис. 5.14, где в сравнении с рис. 5.4 ассоциативное параллельное по разрядам и последовательное по словам ЗУ [115, 116] с организацией  используется как регистр настройки селектора-мультиплексора с
используется как регистр настройки селектора-мультиплексора с 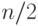
 -входами.
-входами.
Классические для DD- ассоциативных конструкций [115] бит-операции "маскирование" ( AND ), "маскирование с инверсией" ( NAND ) или "маскирование с условной инверсией" ( XOR ) также можно представить в PD- ассоциативном виде:
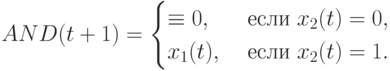 |
( 5.33) |
 |
( 5.34) |
 |
( 5.35) |
где ассоциативной для пользователя считается "управляющая" переменная  .
.
Несмотря на кажущееся усложнение записи (правая часть (5.33)- (5.35)), PD- ассоциативная форма удобна тем, что раскрывает подстановочные механизмы реализации логических функций 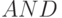 ,
, 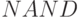 и
и  в нанометровых вычислителях, где на уровне квантовых процессов можно задействовать высокодинамичные реакции замещения, зависящие от некоторого комплекса внешних условий, кодируемого переменной
в нанометровых вычислителях, где на уровне квантовых процессов можно задействовать высокодинамичные реакции замещения, зависящие от некоторого комплекса внешних условий, кодируемого переменной  .
.
Поэтому схемотехническая ценность форм записи (5.33)-(5.35) состоит в том, что в квантовых системах для вычислительных нужд можно использовать не только традиционные для твердотельной микро- и оптоэлектроники методы и средства управления параметрами (значениями токов, интенсивностями потоков фотонов, напряжениями и т. п.), но и методы и средства структурной адаптации атомарных или (макро)моле-кулярных структур по крайней мере подстановочного типа.
Из (5.33)-(5.35), в частности, следует, что для перехода от DD- ассоциативной формы записи к эквивалентной PD- ассоциативной форме достаточно воспользоваться разложением Шеннона для булевых функций  переменных:
переменных:
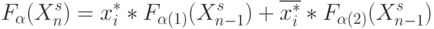 |
( 5.36) |
где выделенная "свободная" переменная  играет управляющую роль в переходе от
играет управляющую роль в переходе от  к
к  .
.
Продолжив процедуру (5.36) до 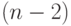 переменных и далее, получим, что в PD- ассоциативных конструкциях в качестве управляющих могут выступать не только отдельные переменные, но и вектора, с ростом размерности которых понижается уровень "элементарности" маскируемых ими функций.
переменных и далее, получим, что в PD- ассоциативных конструкциях в качестве управляющих могут выступать не только отдельные переменные, но и вектора, с ростом размерности которых понижается уровень "элементарности" маскируемых ими функций.
В нанометровых и супрамолекулярных вычислителях при построении PD- ассоциативных конструкций более фундаментальную роль может сыграть разложение Колмогорова [131] непрерывной функции  переменных:
переменных:
где  и
и 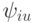 - некоторые непрерывные функции одной переменной, на которые не налагаются какие-либо дополнительные ограничения.
- некоторые непрерывные функции одной переменной, на которые не налагаются какие-либо дополнительные ограничения.
Такое положение вещей является объективной предпосылкой эффективного использования PD- ассоциативных конструкций в процессе высокодинамичного синтеза квантового "рабочего тела" для проблемно-ориентированных нанометровых или супрамолекулярных вычислителей.
В этом случае:
- физико-химический синтез нанометрового или супрамолекулярного вычислителя становится составной частью вычислительного процесса, совмещается с ним в пространстве и во времени и запускается после активизации поток-инструкции пользователя, что соответствует режиму интерпретации программ в традиционных вычислителях;
- предшествующий такому синтезу уровень деструкции "рабочего тела" вычислителя-предка тем глубже, чем выше размерность PD-ассоциативного управляющего вектора в вычислителе-потомке. Таким образом, основное преимущество PD- ассоциативных конструкций и основанных на них вычислительных технологий состоит в том, что они инвариантны физико-техническим условиям работы как субмикронных, так и нанометровых аппаратных платформ. При этом обеспечивают плавный переход вычислительной техники в нанометровую или супрамолекулярную область с квантовым "рабочим телом" с минимальными системотехническими издержками, связанными с реконструкцией или заменой инструментальных средств.
Системотехнические выводы по лекции 5
- Многофункциональность используемых в вычислительной технике операционных модулей является атрибутом всех программируемых изделий, в которых функция пользователя реализуется некоторой частично упорядоченной последовательностью "элементарных" функций, составляющих формально-логическую основу вычислительного процесса.
- Частичная упорядоченность последовательности исполняемых "элементарных" функций предполагает совмещение во времени и пространстве двух процессов, один из которых принято считать вычислительным, а другой - перечислительным. Последний в традиционной вычислительной технике реализуется методами и средствами адресации инициализируемых инструкций и преобразуемых ими данных. В результате любая традиционная ЭВМ работает по правилу: "делай то, что расположено по адресу … над тем, что расположено по адресу …".
- Если в традиционной вычислительной технике объектами перечисления являются ассемблерные инструкции, в своем большинстве реализуемые независимыми операционными блоками (сумматор, умножитель, делитель и т. п.), то в нейроподобной вычислительной технике объектами перечисления уже являются логические функции, изменение которых приводит к изменению функции, реализуемой всей сетью. Поэтому в традиционной вычислительной технике изменение функций операционных устройств осуществляется (в основном) методами и средствами коммутации входов-выходов специализированных операционных блоков и составляющих их узлов, а в нейроподобной вычислительной технике - переназначением параметров настройки отдельных формальных нейронов: пороговых и весовых векторов, а также правил подстановки выходных значений заданной логической функции.
- В нейроподобных многофункциональных модулях перечислительный процесс сопряжен с нарушением некоторого отношения порядка, что требует знания структуры пространства изменения непрерывных параметров (пороговых и весовых векторов).
- Канонической схеме перечисления всех дискретных функций некоторого класса отвечает теоретико-групповая система преобразований, которая основана на отношении эквизначности. Как и в формальных нейронах, в многофункциональных дискретных модулях переход от одной функции к другой сопровождается переходом от одного отношения эквизначности к другому.
- Перечислительный процесс можно выполнить как на основе "ассоциации по сходству", так и на основе "ассоциации по отличию", причем обе ассоциации можно совместить в одном перечислительном процессе.
- Многоконтурное управление многофункциональными модулями в своей основе избыточно, и минимизация такой объективно избыточности требует перехода к одноконтурным схемам управления, которое проще всего сконцентрировать в выходном контуре многофункционального модуля, где осуществляется подстановка значений реализуемой функции.
- Объективно существующий структурно-функциональный и кодовый дуализм между управляющими и информационными потоками предопределяет эффективность использования PD -ассоциативных методов управления, особенно в многопроцессорных вычислительных системах МКМД-типа, которые критичны к процедурам инициализации и распределения потоков инструкций. В таких условиях
PD -ассоциативное управление позволяет без обращения к внешней памяти модифицировать в реальном времени инструкцию с помощью специально организованного потока данных, закрепленную за локальным вычислителем. Однако PD -ассоциативное управление критично к информационным и аппаратным "сбоям". Вместе с тем такое управление адекватно условиям работы нанометровых и супрамолекулярных вычислителей, в которых "тирания" паразитных полимодальных квантовых взаимодействий способна изменить реализуемую функцию.