Базовые положения теории многофункциональных логических модулей
5.5. PD-ассоциативные конструкции и дуализм между потоками инструкций и данных
Наличие в вычислительной технике многофункциональных модулей со смешанными информационными и управляющими входами уже само по себе указывает на существование естественного структурно-функционального дуализма между потоками инструкций и данных. Такой дуализм, с одной стороны, влияет на стратегию синтеза схем из универсальных дискретных модулей, а с другой стороны - раскрывает механизмы управления гиперизбыточными многофункциональными системами типа реальных нейронов и их ансамблей.
Гиперизбыточность реальных нейронов усложняет не только проблему однозначного задания требуемой функции 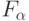 , но и проблему выделения под ее реализацию некоторой (морфологической) структуры. В частности, требуется в реальном времени решить вопрос о формировании адекватной пары "стимул - реакция" на основе одного (конвергентного [25, 128]) нейрона или на основе нейронного ансамбля [129]. Далее требуется локализовать такой нейрон или ансамбль, ориентировать по входам-выходам сеть преобразования и передачи данных, зафиксировать пространственно-временные связи в ансамбле и т. д.
, но и проблему выделения под ее реализацию некоторой (морфологической) структуры. В частности, требуется в реальном времени решить вопрос о формировании адекватной пары "стимул - реакция" на основе одного (конвергентного [25, 128]) нейрона или на основе нейронного ансамбля [129]. Далее требуется локализовать такой нейрон или ансамбль, ориентировать по входам-выходам сеть преобразования и передачи данных, зафиксировать пространственно-временные связи в ансамбле и т. д.
С формальных позиций размерность подобного рода задач настройки сети уже из 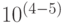 нейронов, имеющих по
нейронов, имеющих по  входов каждый, вновь приводит к гиперкомбинаторным "коммутационным" цифрам даже для морфологически ориентированной по входам-выходам периферической нервной системы. В корковых образованиях, элементы которых связаны по принципу "каждый с каждым", размерность задачи управления не снижается. Она просто трансформируется из задачи структурной адаптации сети в ее параметрическую адаптацию.
входов каждый, вновь приводит к гиперкомбинаторным "коммутационным" цифрам даже для морфологически ориентированной по входам-выходам периферической нервной системы. В корковых образованиях, элементы которых связаны по принципу "каждый с каждым", размерность задачи управления не снижается. Она просто трансформируется из задачи структурной адаптации сети в ее параметрическую адаптацию.
В биологических системах традиционная для техники задача минимизации оборудования, как правило, стоит на втором плане и решается после установления устойчивой связи "стимул - реакция", причем делается это далеко не каждой особью, поставленной в одни и те же (экспериментальные) условия [112].
Поэтому можно считать, что в биосистемах ответ на вопрос о принадлежности требуемой функции 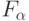 к тому или иному классу
к тому или иному классу 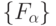 находится на основе анализа существенно неминимальной нейросети, пространственно-временная ориентация которой на начальном этапе адаптации осуществляется простейшими рекуррентными методами, обеспечивающими полноту сети к более широкому по (
находится на основе анализа существенно неминимальной нейросети, пространственно-временная ориентация которой на начальном этапе адаптации осуществляется простейшими рекуррентными методами, обеспечивающими полноту сети к более широкому по (  ,
, 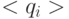 ,
,  ) классу функций, чем составляющие ее УДМ.
) классу функций, чем составляющие ее УДМ.
Отвечающую описанным условиям рекуррентную процедуру построения УДМ ( 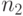 ,
, 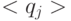 ,
,  ) из УДМ (
) из УДМ ( 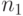 ,
, 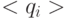 ,
, 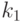 ) получим, опираясь на теорему
) получим, опираясь на теорему
Стоуна [121] и учитывая, что классы функций (5.2) с большими значениями параметров (  ,
,  ,
,  ) включают в себя классы функций с меньшими значениями тех же параметров.
) включают в себя классы функций с меньшими значениями тех же параметров.
Рекуррентную процедуру сначала определим по параметру  для классов двузначных ЛФ
(
для классов двузначных ЛФ
( 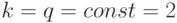 ), а затем распространим ее на многозначные (дискретные) функции типа (5.2).
), а затем распространим ее на многозначные (дискретные) функции типа (5.2).
Пусть имеется ( 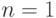 ) двузначный УДМ с одним входом, последовательно настраиваемый на ЛФ: "тождественный ноль" -
) двузначный УДМ с одним входом, последовательно настраиваемый на ЛФ: "тождественный ноль" - 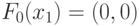 ;
; 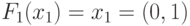 ;
; 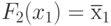 и
и 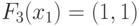 - "тождественная единица".
- "тождественная единица".
В этом случае множество всевозможных подмножеств входных векторов содержит: подмножество "пусто" - 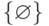 ,
, 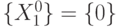 ,
, 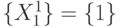 , и
, и 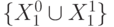 - "единица" множества, а
- "единица" множества, а 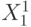 - теоретико-множественное объединение.
- теоретико-множественное объединение.
Тривиальное отображение 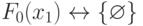 ,
,  ,
,  и
и 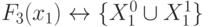 задает мономорфизм этого класса ЛФ на множество всевозможных подмножеств входных векторов, причем дополнение каждой ЛФ до ЛФ "тождественная единица" переводится в соответствующее дополнение вектора
задает мономорфизм этого класса ЛФ на множество всевозможных подмножеств входных векторов, причем дополнение каждой ЛФ до ЛФ "тождественная единица" переводится в соответствующее дополнение вектора 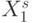 до "единичного" вектора
до "единичного" вектора  .
.
Имея в виду этот мономорфизм, можно записать:
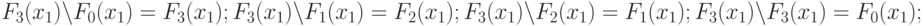
где 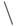 - теоретико-множественное дополнение.
- теоретико-множественное дополнение.
Отсюда, элементарный (с одним входом) УДМ можно описать теоретико-множественным соотношением:
 |
( 5.28) |
Из (5.28) следует, что в элементарном УДМ (ЭУДМ) объектом адаптации является та его часть, где реализуется 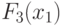 , а сам процесс адаптации сводится к доопределению
, а сам процесс адаптации сводится к доопределению 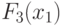 до заданной
до заданной 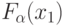 , что и составляет суть разложения Шеннона ЛФ "тождественная единица", которое используется при построении двузначных УДМ [101].
, что и составляет суть разложения Шеннона ЛФ "тождественная единица", которое используется при построении двузначных УДМ [101].
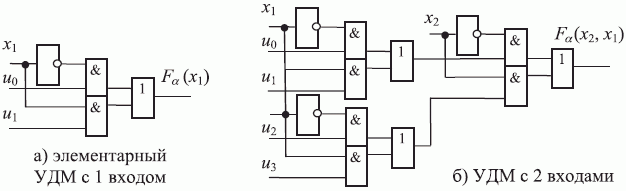
В ЭУДМ (рис. 5.10-а) дешифратор представляет собой инвертор, а управление селектором-мультиплексором выполняется по входам 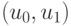 , причем регистр управления RG не показан (ср. с рис. 5.7).
, причем регистр управления RG не показан (ср. с рис. 5.7).
Чтобы распространить (5.28) на класс двумерных двузначных ЛФ, используем тривиальную а-нумерацию табл. 5.6 и мономорфизм:
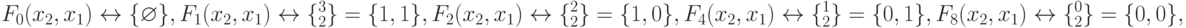
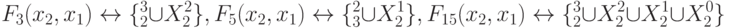
и т. д. до 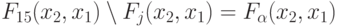 ,
,
В результате двухвходовой двузначный УДМ (УДМ2) можно описать теоретико-множественным соотношением:
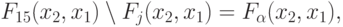 |
( 5.29) |
где 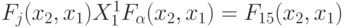
Этому соотношению отвечает схема УДМ2 рис. 5.10-б, которая содержит три ЭУДМ и настраивается по входам  в соответствии с тривиальной а-нумерацией табл. 5.4.
в соответствии с тривиальной а-нумерацией табл. 5.4.
При синтезе логических схем 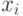 -входы обычно считают информационными (
-входы обычно считают информационными (  -входы), а
-входы), а 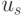 -входы - управляющими (
-входы - управляющими (  -входы).
-входы).
Сравнив схемы ЭУДМ и УДМ2, можно ввести рекуррентную проце-дуру построения УДМ на n входов (УДМ ):
Шаг 1. Чтобы получить УДМn, необходимо выходы двух параллельно соединенных  -входами УДМn-1 подать на
-входами УДМn-1 подать на  -входы ЭУДМ, на
-входы ЭУДМ, на  -входы кото-рого необходимо подать переменные
-входы кото-рого необходимо подать переменные 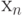 и
и 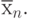
Шаг 2. Шаг 1 повторить для УДМn-1 и перейти к УДМn-2, и т. д. до УДМ2.
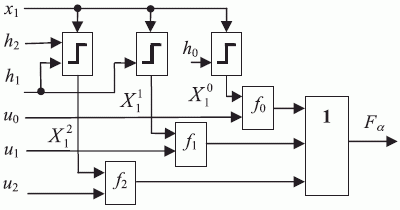
Схему ЭУДМ и процедуру построения многозначных (в частности, трехзначных - рис. 5.11) УДМ можно получить, приняв:
- Входной дешифратор формирует "единичный" выход в соответствии со следующим (пороговым) правилом:

- Схемы "И" селектора-мультиплексора работают по правилу:
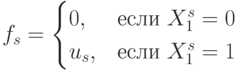
- Схема "ИЛИ" селектора-мультиплексора работает по классическому многозначному правилу:
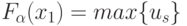 .
.
Правила настройки трехзначного ЭУДМ соответствуют тривиальной  -нумерации трехзначных ЛФ табл. 5.6, где компоненты вектора
-нумерации трехзначных ЛФ табл. 5.6, где компоненты вектора 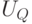 считаются заданными в трехзначном алфавите, причем правила работы ЭУДМ рис. 5.11 пригодны для произвольного алфавита
считаются заданными в трехзначном алфавите, причем правила работы ЭУДМ рис. 5.11 пригодны для произвольного алфавита 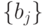 мощности три.
мощности три.
 |
 |
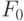 |
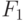 |
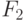 |
 |
 |
 |
 |
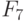 |
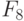 |
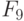 |
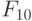 |
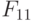 |
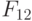 |
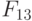 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 1 | 1 | 1 | 1 |
| 1 | 1 | 0 | 0 | 0 | 1 | 1 | 1 | 2 | 2 | 2 | 0 | 0 | 0 | 1 | 1 |
| 2 | 2 | 0 | 1 | 2 | 0 | 1 | 2 | 0 | 1 | 2 | 0 | 1 | 2 | 0 | 1 |
 |
 |
0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 1 | 1 | 1 | 1 |
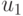 |
0 | 0 | 0 | 1 | 1 | 1 | 2 | 2 | 2 | 0 | 0 | 0 | 1 | 1 | |
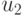 |
0 | 1 | 2 | 0 | 1 | 2 | 0 | 1 | 2 | 0 | 1 | 2 | 0 | 1 | |
 |
 |
 |
 |
 |
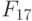 |
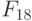 |
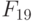 |
 |
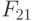 |
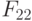 |
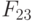 |
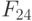 |
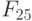 |
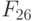 |
|
| 0 | 0 | 1 | 1 | 1 | 1 | 2 | 2 | 2 | 2 | 2 | 2 | 2 | 2 | 2 | |
| 1 | 1 | 1 | 2 | 2 | 2 | 0 | 0 | 0 | 1 | 1 | 1 | 2 | 2 | 2 | |
| 2 | 2 | 2 | 0 | 1 | 2 | 0 | 1 | 2 | 0 | 1 | 2 | 0 | 1 | 2 | |
 |
 |
1 | 1 | 1 | 2 | 2 | 2 | 2 | 2 | 2 | 2 | 2 | 2 | 2 | |
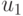 |
1 | 2 | 2 | 2 | 0 | 0 | 0 | 1 | 1 | 1 | 2 | 2 | 2 | ||
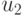 |
2 | 0 | 1 | 2 | 0 | 1 | 2 | 0 | 1 | 2 | 0 | 1 | 2 |
Схема ЭУДМ рис. 5.11 удовлетворяет рекуррентной процедуре "коммутационного" наращивания до УДМn с той разницей, что  -входами параллельно объединяются три УДМn-1.
-входами параллельно объединяются три УДМn-1.
Схемы рисунков 5.10 и 5.11 являются селекторами-мультиплексорами, в которых управляющими принято считать  -входы, а информационными -
-входы, а информационными -  -входы, то есть в зависимости от интерпретации УДМ как комбинационного или коммутационного автомата меняется только представление об информационных и управляющих переменных или параметрах, но не сама схема УДМ.
-входы, то есть в зависимости от интерпретации УДМ как комбинационного или коммутационного автомата меняется только представление об информационных и управляющих переменных или параметрах, но не сама схема УДМ.
Такой структурно-функциональный дуализм между управляющими и информационными переменными проявляется и в формальной записи 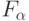 типа (5.13):
типа (5.13):
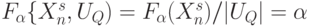 , или
, или 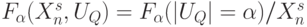 при
при  .
.
Обе записи задают одну и ту же 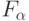 , но отличаются "перечисляющими" переменными в условии настройки. В первом случае УДМ рассматривается как комбинационный автомат, выходная реакция которого зависит от содержимого
, но отличаются "перечисляющими" переменными в условии настройки. В первом случае УДМ рассматривается как комбинационный автомат, выходная реакция которого зависит от содержимого  -входов, доопределяемых
-входов, доопределяемых  -входами. Во втором случае УДМ рассматривается как коммутационный автомат, выходная реакция которого зависит от содержимого
-входами. Во втором случае УДМ рассматривается как коммутационный автомат, выходная реакция которого зависит от содержимого  -разряда регистра, возбужденного комбинацией значений соответствующих
-разряда регистра, возбужденного комбинацией значений соответствующих  -входов.
-входов.
В сочетании с "кодовым" фон-неймановским дуализмом, предполагающим единообразное двоичное представление потоков инструкций и данных в ЭВМ, вскрытый структурно-функциональный и формальный дуализм предполагает возможность арифметико-логических преобразований как потоков данных, так и потоков инструкций.
В сочетании с аналого-цифровым дуализмом данный дуализм позволяет рассматривать оперативное управление вычислителями как ассоциативный процесс, в котором реализуемая операционным устройством функция зависит от содержимого потока данных ( PD- ассоциативность). Такая зависимость позволяет эффективно управлять в реальном времени (сверх)большим коллективом, начиная с микрокомандного (бит-процессорного) уровня организации вычислений, если в схему АЛУ каждого бит-процессора заложить схемотехнические решения, обеспечивающие модификацию исполняемой бит-операции под воздействием потоков обрабатываемых данных. Наиболее удобно такое (сверхоперативное управление (микро)командами реализовать в синхронной, конвейерной арифметике, где "вес" разряда определяется его положением на оси времени, а выполнение каждой бит-инструкции сопровождается принудительной задержкой на 1 такт. В этом случае в однобитное конвейерное АЛУ каждого бит-процессора при проектировании и изготовлении бит-матричных СБИС закладываются специальные PD- ассоциативные конструкции.