Нейросетевые информационные модели сложных инженерных систем
Полезность того или иного представления решения может определиться только в контексте конкретного приложения. Для системы, предупреждающей о высокой ошибке решения в области некорректности, по-видимому, следует предпочесть результат сети встречного распространения (рис. 4.6), так искажения решения в областях, где это решение имеет смысл, минимальны.
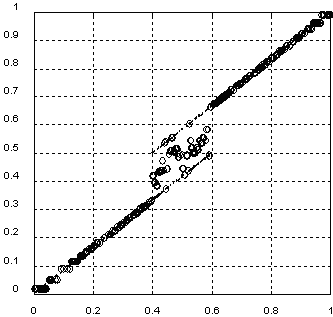
Рис. 4.6. Кусочно-постоянное в области регулярности решение некорректной обратной задачи, полученное с помощью сети встречного распространения (см. подпись и обозначения на Рис.4.5).
Обратимся теперь к изучению возможности автоматического выделения области некорректности. В нейронной сети встречного распространения кластеры, расположенные в области некорректности задачи будут содержать близкие вектора, для которых значения моделируемой функции относятся к разным ветвям неоднозначности. Персептрон выходного слоя нейросети в этом случае будет обучаться среднему значению на векторах кластера, поэтому ошибка обучения останется конечной.
В приведенном примере, при h=0.2, теоретическое значение предельной ошибки обучения (среднеквадратичное уклонение) для данных одного кластера равно 0.1. Распределение ошибки по кластерам, наблюдаемое в расчетах, приведено на рис. 4.7. Область некорректности может быть легко автоматически выделена при помощи простого решающего правила.
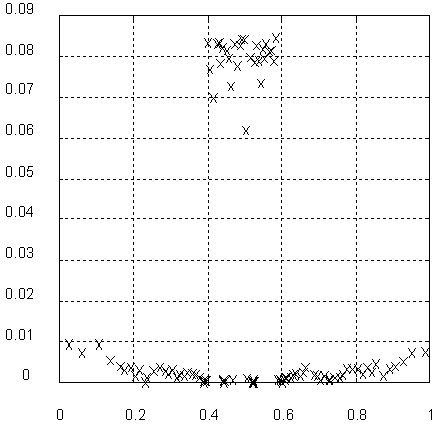
Рис. 4.7. Распределение ошибки обучения по пространственным кластерам Карты самоорганизации Кохонена с легко выделяемой областью некорректности задачи.
Подведем некоторые итоги рассмотрения модельных задач. Можно выделить два основных пути применения нейронных сетей встречного распространения для решения обратных и комбинированных некорректно поставленных задач.
Во-первых, слой самоорганизующихся нейронов карты Кохонена позволяет получить локальную дифференциальную оценку степени некорректности задачи и пространственное распределение ошибки обобщения, делаемой сетью. Кластерное разложение одинаково легко выполняется в признаковых пространствах любой размерности.
Алгоритм кластеризации Кохонена легко обобщается на случай наличия пропусков в данных. Поскольку для отнесения некоторого вектора к кластеру требуется лишь вычислить Евклидово расстояние между этим вектором и текущим приближением к центроиду кластера, и найти кластер с минимальным расстоянием, то при наличии пропущенных компонент в векторе расстояние можно вычислять по имеющимся компонентам. Это эквивалентно поиску ближайшего кластера в подпространстве известных компонент. Замечательно, что сеть встречного распространения может обучаться даже если в каждом обучающем векторе имеются пропущенные компоненты. При этом не требуется заполнения пропусков искусственными значениями.
Второй прикладной аспект состоит в том, что в областях корректности задачи решение, даваемое сетью встречного распространения является весьма точным. Это связано с локальным характером обучения в пределах каждого кластера, и, соответственно отсутствием эффектов равномерного распределения ошибки по кластерам. В этом смысле, регуляризующий эффект сети встречного распространения меньше, нежели у традиционной многослойной сети с обратным распространением.
