НОУ ИНТУИТ | Введение в информатику. Лекция 5: Игры. Клеточные автоматы

Учитесь и получайте официальные документы БЕСПЛАТНО. Вы можете поддержать наш проект.

Регистрация Вход

Твой путь к знаниям!

Российский государственный гуманитарный университет

Опубликован: 13.07.2022 | Доступ: свободный | Студентов: 343 / 38 | Длительность: 11:54:00

Темы: Программирование, Образование, Школа

Специальности: Программист

|

Вам нравится? Нравится 8 студентам

| Поделиться |

Поддержать курс

Пример 6. Рассмотрим игру, которая является обобщением игры из примера 5. Она заключается в следующем. Имеется n кучек. Два игрока ходят по очереди. За один ход игрок может взять от 1 до 3 камней из любой кучки. Выигрывает тот, кто берет последний камень.

Пусть кучка i содержит xi камней, для $i = 1, 2, \dots, n$ . По теореме, функция Шпрага-Гранди для этой игры имеет вид:

$g(x_1, x_2, \dots, x_n) = x_1 \mod 4 \oplus x_2 \mod 4 \oplus \dots \oplus x_n \mod 4.$

Поэтому позиция является проигрышной тогда и только тогда, когда побитовая строгая дизъюнкция остатков от деления на 4 чисел x_i равна 0, для $i = 1, 2, \dots, n$ .

Найдем выигрышную стратегию игры. Заметим, что свойство позиции быть выигрышной или проигрышной зависит только от двух младших разрядов двоичного представления чисел x_i , для $i = 1, 2, \dots, n$ .

Положим $x = x_1 \mod 4 \oplus x_2 \mod 4 \oplus \dots\oplus x_n \mod 4$ .

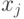Очевидно, что $x \le 3$ . Пусть $x \ne 0$ и i - старший разряд двоичного представления числа x, значение которого равно 1. Тогда существует число x_j , в i-ом разряде двоичного представления которого стоит 1, так как i-ым является один из двух младших разрядов.

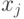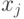Заметим, что значения двоичных разрядов, старших i, чисел x_j и $x \oplus x_j$ совпадают, при этом в разряде i числа x_j стоит 1, а в том же разряде числа $x \oplus x_j$ стоит 0. Отсюда следует, что, во-первых, $x \oplus x_j < x_j$ и что, во-вторых, $x_j - x \oplus x_j \le 3$ .

Заметим также, что $(x \oplus x_j) \mod 4 = x \oplus (x_j \mod 4)$ , так как $x \le 3$ . Следовательно,

$x_1 \mod 4 \oplus \dots \oplus (x \oplus x_j) \mod 4 \oplus \dots \oplus x_n \mod 4 = \\ = x \oplus (x_1 \mod 4 \oplus \dots \oplus x_j \mod 4 \oplus \dots \oplus x_n \mod 4) = x \oplus x = 0.$

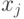Таким образом, выигрышный ход - взять ( $x_j - x \oplus x_j$ ) камней из кучки, в которой находится x_j камней.

Например, пусть кучки содержат 9, 6, 5 и 4 камня. Тогда 9 mod 4 \oplus 6 mod 4 \oplus 5 mod 4 \oplus 4 mod 4 = 1 \oplus 2 \oplus 1 \oplus 0 = 2.

Следовательно, позиция является выигрышной. Номер старшего ненулевого двоичного разряда числа 2 равен 1. Этот же разряд является ненулевым у числа 6. Имеем: $6 - 2 \oplus 6 = 6 - 4 = 2$ . Поэтому выигрышный ход состоит в том, чтобы взять 2 камня из кучки, содержащей 6 камней.

Проигрышные позиции игры "Ним" с тремя кучками

Проигрышные позиции в игре "Ним" с тремя кучками обладают интересными свойствами.

Рассмотрим метод поиска проигрышных позиций для игры "Ним" с тремя кучками, который является сочетанием методов из п. 5.1.2 и 5.1.4.

Проигрышные позиции с ненулевыми упорядоченными значениями компонент можно построить с помощью таблицы сложения для операции $\oplus$ (см. ниже), так как число камней в третьей кучке равно результату применения операции \oplus к числу камней в первой и второй кучках. Эти позиции имеют вид:

(1, 2k, 2k + 1);
(2, 4k, 4k + 2);				(3, 4k, 4k + 3);
(2, 4k + 1, 4k + 3);				(3, 4k + 1, 4k + 2);
(4, 8k, 8k + 4);				(5, 8k, 8k + 5);
(4, 8k + 1, 8k + 5);				(5, 8k + 1, 8k + 4);
(4, 8k + 2, 8k + 6);				(5, 8k + 2, 8k + 7);
(4, 8k + 3, 8k + 7);				(5, 8k + 3, 8k + 6);
(6, 8k, 8k + 6);				(7, 8k, 8k + 7);
(6, 8k + 1, 8k + 7);				(7, 8k + 1, 8k + 6);
(6, 8k + 2, 8k + 4);				(7, 8k + 2, 8k + 5);
(6, 8k + 3, 8k + 5);				(7, 8k + 3, 8k + 4);
…

для 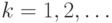$k = 1, 2, \dots$ При фиксированном значении k проигрышные позиции находятся с помощью двоичного представления чисел, равных количеству камней в первых двух кучках. Например, при k = 1 для числа камней в первых двух кучках имеем:

 1		 1 		 1  		 1   
10		10 		10  		10    ...

Вместо знака следует подставлять значения 0 и 1. Соответственно, при k = 1 имеется одна позиция, первая компонента в которой равна 1, четыре позиции, первая компонента которых равна 2 или 3, и 16 позиций, первая компонента которых равна 4, 5, 6 или 7, и так далее.

Соответственно, при k = 2 двоичное представление числа камней в первых двух (наименьших) кучках имеет вид:

 1		 1 		 1  		 1   
100		100 		100  		100    ...

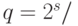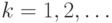В общем случае, для целого неотрицательного s положим q = 2^s/ и $p = 2^{s + 1}$ . Тогда проигрышными являются позиции, первая компонента которых равна $q, q + 1, \dots, 2q - 1$ , вторая компонента принимает значения $pk, pk + 1, \dots, pk + q - 1$ , для $k = 1, 2, \dots$ , а третья компонента равна результату применения операции bitXor к первым двум компонентам.

Таким образом, пусть m - минимальное число камней в трех кучках, p - наименьшая степень 2, такая что m < p, и $q=\fracp2$ . Тогда проигрышные позиции, содержащие m, находятся следующим образом:

$(m, pk, pk + m),\\ (m, pk + 1, pk + (m \oplus 1)), \\ \dots, \\ (m, pk + q - 1, pk + (m \oplus (q - 1))),\\ для k = 1, 2, \dots$

Пример 7. Пусть m = 10, тогда p = 16 и q = 8. Проигрышные позиции с минимальным числом камней в трех кучках, равным 10, имеют вид:

(10, 16k, 16k + 10), 			(10, 16k + 4, 16k + 14),
(10, 16k + 1, 16k + 11), 			(10, 16k + 5, 16k + 15),
(10, 16k + 2, 16k + 8),			(10, 16k + 6, 16k + 12),
(10, 16k + 3, 16k + 9), 			(10, 16k + 7, 16k + 13),

для 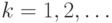$k = 1, 2, \dots$ , или

$(10, 16, 26), (10, 17, 27), (10, 18, 24), (10, 19, 25), (10, 20, 30), (10, 21, 31), (10, 22, 28), (10, 23, 29), (10, 32, 42), (10, 33, 43), \dots$

Рассмотрим таблицу сложения для операции $\oplus$ , которая используется для построения проигрышных позиций в игре с тремя кучками: найдем значения $x \oplus y$ , для $x = q, q + 1, \dots, 2q - 1$ и $y = 0, 1, \dots, q - 1$ , где q = 2^s , для целого положительного числа s. Таблицы сложения для значений q, равных 2, 4 и 8 приведены в рис. 5.2.

Рис. 5.2. Таблица сложения для операции разделительной дизъюнкции

Из свойств побитовой операции строгой дизъюнкции следует, что таблицы сложения в данном случае можно строить по определенному правилу, без вычисления двоичных представлений чисел x и y. Достаточно использовать схему, приведенную на рис. 5.3.

Рис. 5.3. Схема для заполнения рис. 5.2

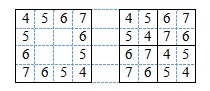
Схема применяется следующим образом. Заполнение таблиц начинается из углов, обозначенных жирными черными точками. В них помещается значение q. В направлениях, указанных стрелками, значения элементов таблицы увеличиваются на 1 в каждом столбце или строке. После заполнения крайних рядов, таблица делится на 4 равные по размеру квадратные подтаблицы, а затем та же схема применяется для заполнения пустых ячеек каждой из полученных таблиц (см. рис. 5.2). Заметим также, что, как элементы главной диагонали, так и элементы побочной диагонали каждой таблицы равны между собой. Например, для q = 4 получится результат, приведенный в рис. 5.4.

Рис. 5.4. Построение таблицы сложения операции разделительной дизъюнкции при q = 4

Нетрудно заметить, что таблицы могут быть построены итеративно: текущая таблица получается из предыдущей заменой каждой ее ячейки таблицей 2 * 2 по правилу

$(n) \to \begin{pmatrix} 2n&2n+1\\ 2n+1&2n \end{pmatrix}$

при этом нулевой является таблица (1). Если одинаковые числа заменить квадратами одинакового цвета, то при q = 64 получится один из вариантов раскраски квадрата, приведенный на рис. 5.5.

Рис. 5.5. "Цветовое" представление таблицы сложения операции разделительной дизъюнкции при q = 64

Дальше >>

Авторизоваться

Введение в информатику

Игры. Клеточные автоматы

Проигрышные позиции игры "Ним" с тремя кучками

Вопросы и ответы