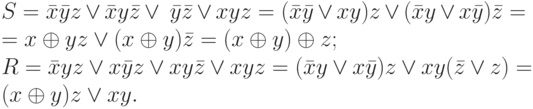Логические основы компьютера

Электронные логические схемы

Электронная логическая схема состоит из базовых логических элементов, или вентилей. Логический элемент (logic gate) - это логическая функция, которая преобразует входные сигналы (значения аргументов) в выходной сигнал (значение функции).

Логический уровень сигнала представлен в виде уровня напряжения, попадающего в один из двух диапазонов, где 0 используется для низкого напряжения, а 1 - для высокого. При создании цифровой схемы вентили соединяются между собой, при этом их выходы подключаются к входам других вентилей.

Базовый логический элемент выполняет одну логическую операцию - отрицание, конъюнкцию, дизъюнкцию, штрих Шеффера, стрелку Пирса, строгую дизъюнкцию или эквиваленцию. Множество электронных схем образует булеву алгебру (алгебру релейных схем), поэтому для сокращения схем применяют законы булевой алгебры (см. п. 4.1).

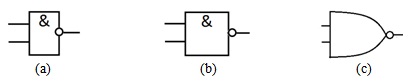
Ниже перечисляются базовые логические элементы. Для каждого из них приводятся три вида обозначений: обозначения ГОСТ, обозначения Международной электротехнической комиссии (англ. IEC - International electrotechnical commission) и обозначения ANSI. Входные сигналы показаны слева, а выходные справа.

В дальнейшем для построения логических схем используются обозначения ГОСТ.

Схема НЕ

На рис. 4.2 приведена схема НЕ (NOT gate), или инвертора - логического отрицания, соответствующего логической функции .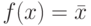

Рис. 4.2. Инвертор: (a) ГОСТ; (b) IEC; (c) ANSI

Схема повторителя

На рис. 4.3 приведена схема повторителя (BUFFER): .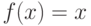

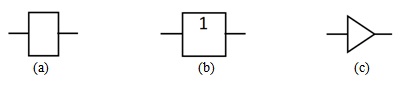
Рис. 4.3. Повторитель: (a) ГОСТ; (b) IEC; (c) ANSI

Схема И

Схема И (AND gate) соответствует логической конъюнкции: ( рис. 4.4).

Рис. 4.4. Схема И: (a) ГОСТ; (b) IEC; (c) ANSI

Схема ИЛИ

Рис. 4.5. Схема ИЛИ: (a) ГОСТ; (b) IEC; (c) ANSI

На рис. 4.5 приведена схема ИЛИ (OR gate) - логической дизъюнкции:.

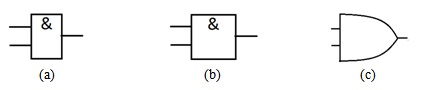
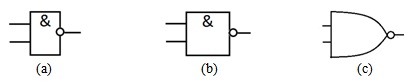
Схема И-НЕ

Схема И-НЕ (NAND gate) соответствует штриху Шеффера, или отрицанию конъюнкции: ( рис. 4.6).

Рис. 4.6. Схема И-НЕ: (a) ГОСТ; (b) IEC; (c) ANSI

Схема ИЛИ-НЕ

На рис. 4.7 приведена схема ИЛИ-НЕ (NOR gate) - стрелки Пирса, или отрицания дизъюнкции: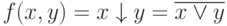

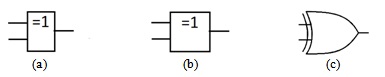
Рис. 4.7. Схема ИЛИ-НЕ: (a) ГОСТ; (b) IEC; (c) ANSI

Схема ИСКЛЮЧАЮЩЕЕ ИЛИ

Схема ИСКЛЮЧАЮЩЕГО ИЛИ (XOR gate) соответствует строгой дизъюнкции: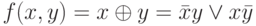 (рис. 4.8).

Рис. 4.8. Схема ИСКЛЮЧАЮЩЕЕ ИЛИ: (a) ГОСТ; (b) IEC; (c) ANSI

Схема ИСКЛЮЧАЮЩЕЕ ИЛИ-НЕ

Заметим, что

Схема ИСКЛЮЧАЮЩЕГО ИЛИ-НЕ (XNOR gate) соответствует эквиваленции 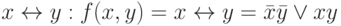( рис. 4.9).

Рис. 4.9. Схема ИСКЛЮЧАЮЩЕЕ ИЛИ-НЕ: (a) ГОСТ; (b) IEC; (c) ANSI

На практике вентили И-НЕ и ИЛИ-НЕ строятся проще, чем вентили И и ИЛИ; кроме того, они могут иметь более двух входов.

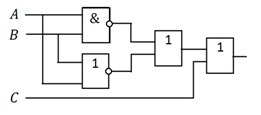
Пример 19. Электронная логическая схема, которая соответствует логической функции , показана на рис. 4.10.

Рис. 4.10. Схема функции

Упростим схему. Имеем:

Поэтому схемы, представленные на рис. 4.10 и 4.11, равносильны.

Рис. 4.11. Схема функции

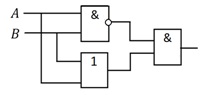
Пример 20. Построим логическую функцию по схеме рис. 4.12.

Рис. 4.12. Схема функции f

Имеем: 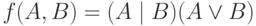. Упростим функцию f ( на рис. 4.8):

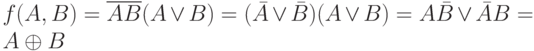
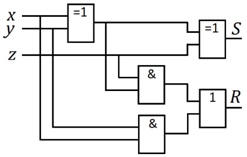
Пример 21. Построим схему одноразрядного сумматора. Имеем:

Ясно, что для реализации сумматора необходима схема с тремя входами: два входа для значений разряда и один - для переноса из предыдущего разряда. Схема должна иметь два выхода, соответствующих значению разряда и переносу в следующий разряд ( рис. 4.13). Такую схему называют полным сумматором. Схема без входного переноса называется полусумматором.

В табл. 4.6 приведена таблица истинности для одноразрядного полного сумматора. В ней параметр z соответствует переносу из предыдущего разряда, S - сумме, а R - переносу в следующий разряд.

По таблице имеем:

Рис. 4.13. Схема полного одноразрядного сумматора: z - вход переноса, S - сумма,R - выход переноса