Введение в информатику
[+]
Российский государственный гуманитарный университет
Опубликован: 13.07.2022 | Доступ: свободный | Студентов: 346 / 38 | Длительность: 11:54:00
Темы: Программирование, Образование, Школа
Специальности: Программист
Лекция 2:

Кодирование чисел и текста
A
|
версия для печати
< Лекция 1 || Лекция 2: 123456 || Лекция 3 >

В остальных разрядах хранится дробная часть мантиссы. Целая часть ненулевой мантиссы всегда равна 1, поэтому она не хранится; говорят, что ее представляет скрытый бит.

Например, пусть для кодирования используется тип данных float. Он содержит 32 разряда. В старшем, 31 разряде, хранится число s. В следующих 8 разрядах хранится смещенный порядок - двоичный код числа 127 + q. Оставшиеся 23 разряда предназначены для хранения дробной части f мантиссы.

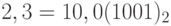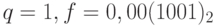Пример 15. Рассмотрим представление в формате float числа 2,3. Имеем: 2,3 = 10,0(1001)_2. Соответственно, нормальная форма числа 2,3 выглядит следующим образом: 2,3 = 1,00(1001)_2 * 2. Следовательно, q = 1, f = 0,00(1001)_2.

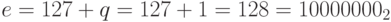Далее, s = 0; e = 127 + q = 127 + 1 = 128 = 1000 0000_2. В последних 23 разрядах хранится приближенное двоичное представление числа f (табл. 2.4). Если значение первого знака, которое не помещается в отведенный набор разрядов, равно 1, то это представление увеличивается на 1. В данном случае этого не происходит, так как первая отбрасываемая цифра равна 0.

Таблица 2.4. Представление числа 2,3 в типе данных float
Порядок e Дробная часть мантиссы f
31 30 29 28 27 26 25 24 23 22 21 20 19 18 17 16 15 14 13 12 11 10 9 8 7 6 5 4 3 2 1 0
0 1 0 0 0 0 0 0 0 0 0 1 0 0 1 1 0 0 1 1 0 0 1 1 0 0 1 1 0 0 1 1

Таким образом, представление 2,3 в типе данных float имеет вид:

0100 0000 0001 0011 0011 0011 0011 0011 = 40133333 (hex).

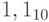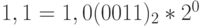Пример 16. Для числа 1,1_{10} имеем: 1,1 = 1,0(0011)_2 * 2^0.

Найдем порядок: 127 + q = 127 = 0111 1111_2. Соответственно, представление в типе данных float имеет вид:

0 0111 1111 000 1100 1100 1100 1100 1101 = 0011 1111 1000 1100 1100 1100 1100 1101 = 3f8ccccd (hex).

Первая отбрасываемая цифра равна 1, поэтому в нулевом разряде хранится 1, а не 0.

Пример 17. Найдем представление в типе данных float первых четырех натуральных чисел. Имеем:

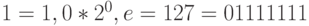  1. 1 = 1,0 * 2^0, e = 127 = 01111111;
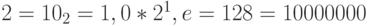  2. 2 = 10_2 = 1,0 * 2^1, e = 128 = 10000000;
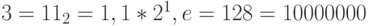  3. 3 = 11_2 = 1,1 * 2^1, e = 128 = 10000000;
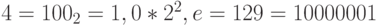  4. 4 = 100_2 = 1,0 * 2^2, e = 129 = 10000001.

Таким образом,

1 (decimal) = 3f800000 (hex); 2 (decimal) = 40000000 (hex); 
3 (decimal) = 40400000 (hex); 4 (decimal) = 40800000 (hex).
Представление нуля и субнормальных чисел. Бесконечность и не-числа

Рассмотрим способы хранения чисел, представленных в форме, отличной от нормальной.

Для числа 0 имеется два представления, 00....0 и 10...0, так что он хранится со знаком, как +0 и как -0. Например, в типе данных float число +0 представлено как 00000000 (hex), а -0 - как 80000000 (hex).

В субнормальном виде хранятся числа, близкие к 0 (табл. 2.5). В двоичном коде таких чисел порядок хранится как последовательность нулей, а дробная часть мантиссы содержит хотя бы один ненулевой знак. Если значение скрытого бита в нормализованных числах равно 1, то в субнормальных числах оно равно 0.

Таблица 2.5. Упорядоченное множество двоичных кодов типа данных float
Код (hex) Десятичное число, \ge 0 Вид числа Десятичное число, \le 0 Код (hex)
00000000 +0 нулевое -0 80000000
00000001 1,401298464e-45 субнормальное -1,401298464e-45 80000001
\dots \dots \dots \dots
007fffff 1,754942107e-38 -1,754942107e-38 807fffff
00800000 1,754943508e-38 нормализованное -1,754943508e-38 80800000
\dots \dots \dots \dots
7f7fffff 3,402823466e+38 -3,402823466e+38 ff7fffff
7f800000 +\infty бесконечное -\infty ff800000
7f800001 NaN не-число NaN ff800001
\dots \dots \dots \dots
7fffffff NaN NaN ffffffff

В свою очередь, двоичный код, в котором порядок представляет собой последовательность единиц, а дробная часть мантиссы - последовательность нулей, используется для хранения бесконечностей - +\infty и -\infty. Например, в типе данных float код 7f800000 (hex) представляет +\infty, а код ff800000 (hex), соответственно, -\infty. Если при этом дробная часть мантиссы содержит хотя бы один знак, значение которого равно 1, то такой код представляет не-число - NaN (от англ. not a number). Выделяют два вида не-чисел - qNaN, от quiet NaN ("тихий"), и sNaN, от signaling NaN ("сигнальный", или "сигнализационный"). В реализациях языков программирования они обычно отличаются старшим битом дробной части мантиссы. Второй из этих видов, как правило, возвращает исключительную ситуацию.

Табл. 2.5 содержит перечисление двоичных кодов от 00000000 до ffffffff, представляющих неотрицательные и неположительные действительные числа в типе данных float, а также бесконечности и не-числа.

Преобразование двоичных кодов в десятичное представление

Для нормализованных чисел преобразование двоичного кода в десятичный формат выполняется по формуле (в обозначениях из п. 2.2.3):

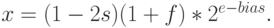
x = (1 - 2s)(1 + f) * 2^{e - bias}.

Пример 18. Найдем действительное число x, которое в типе данных float хранится в виде 47a80000 (hex). По таблице тетрад имеем:

47a80000 (hex) = 0100 0111 1010 1000 0000 0000 0000 0000 = 0 10001111 010 1000 0000 0000 0000 0000.

Найдем порядок: 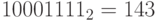10001111_2 = 143. Следовательно,

q = 143 - bias = 143 - 127 = 16.

Теперь найдем мантиссу. Имеем:

1 + f = 1,010 1000 0000 0000 0000 0000 = 1,0101_2.

Таким образом,

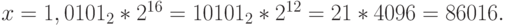
x = 1,0101_2 * 2^{16}= 10101_2 * 2^{12}= 21 * 4096 = 86016.

Для денормализованных чисел преобразование в десятичный формат выполняется следующим образом:

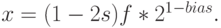
x = (1 - 2s)f * 2^{1 - bias}.

Пример 19. Найдем действительное число x, которое в типе данных float хранится в виде 00700000 (hex). По таблице тетрад получаем:

00700000 (hex) = 0000 0000 0111 0000 0000 0000 0000 0000 = 0 00000000  111 0000 0000 0000 0000 0000.

Заметим, что число является субнормальным. Вычислим порядок и мантиссу: q = 1 - bias = - 126; 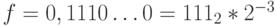f = 0,1110\dots0 = 111_2 * 2^{- 3}.

Таким образом,

x = 7 * 2^{- 129} \approx 0,1028557557 * 10^{- 39}.
Дальше >>
< Лекция 1 || Лекция 2: 123456 || Лекция 3 >

Вопросы и ответы

вопросов: 0