Сжатие информации с потерями
Таким образом, при таком кодировании, если сигнал 1 имеет длительность  , то 0 -
, то 0 - 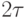 .
.
Рассчитаем емкость этого канала. Нужно рассчитать 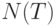 . Пусть
. Пусть 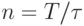 ,
тогда получается, что нужно рассчитать сколькими способами можно разбить
отрезок длины
,
тогда получается, что нужно рассчитать сколькими способами можно разбить
отрезок длины  отрезками длины 2 и 1. Получаем, что
отрезками длины 2 и 1. Получаем, что 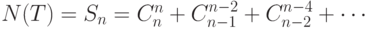 , где
первое слагаемое - это количество способов, которыми можно разбить отрезок длины
, где
первое слагаемое - это количество способов, которыми можно разбить отрезок длины 
 отрезками длины 1, второе слагаемое - это
количество способов, которыми можно разбить отрезок длины
отрезками длины 1, второе слагаемое - это
количество способов, которыми можно разбить отрезок длины 
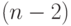 отрезками длины 1 и одним отрезком длины
отрезками длины 1 и одним отрезком длины  , третье слагаемое - это количество способов,
которыми можно разбить отрезок длины
, третье слагаемое - это количество способов,
которыми можно разбить отрезок длины 
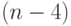 отрезками длины
1 и двумя отрезками длины 2 и т.д. Таким образом,
отрезками длины
1 и двумя отрезками длины 2 и т.д. Таким образом,  . Вследствие того, что
. Вследствие того, что 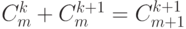 для любых
для любых 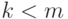 ,
получается, что
,
получается, что
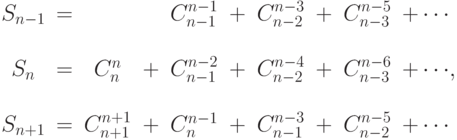
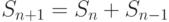 при
при 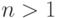 . Если положить, что
. Если положить, что 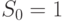 , то
, то 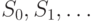 - это последовательность
- это последовательность 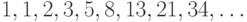 , т.е. числа Фибоначчи.
C XIX века для вычисления
, т.е. числа Фибоначчи.
C XIX века для вычисления  -го члена
последовательности Фибоначчи известна формула
-го члена
последовательности Фибоначчи известна формула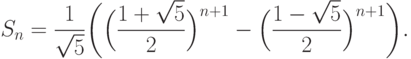
 бод.
бод.При использовании частотной модуляции на практике нули, как правило,
кодируются в два раза плотнее. Это достигается тем, что учитываются не
уровни сигнала, а смена уровня (полярности). Если частота 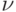 соответствует 1, то с частотой
соответствует 1, то с частотой  производится проверка уровня сигнала. Если
он меняется, то это сигнал 1, если нет, то - 0. На практике
частота
производится проверка уровня сигнала. Если
он меняется, то это сигнал 1, если нет, то - 0. На практике
частота 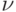 - это частота синхронизации, т.е. частота импульса,
который независимо от данных меняет полярность сигнала. 0 не генерирует импульса
смены полярности, а 1 генерирует (См. рис. 7.3).
- это частота синхронизации, т.е. частота импульса,
который независимо от данных меняет полярность сигнала. 0 не генерирует импульса
смены полярности, а 1 генерирует (См. рис. 7.3).
Для записи информации на первые магнитные диски и ленты использовался метод FM. На гибкие диски 5.25" и 3.5" информация записывается методом MFM (Modified FM) - модификацией метода FM, позволяющей в 2 раза повысить плотность записи. Это достигается тем, что частота синхронизации увеличивается вдвое. MFM можно использовать с теми же физическими каналами, что и FM, потому что импульсы синхронизации не передаются перед 1 и первым 0 в серии нулей (См. рис. 7.4).
Метод записи с групповым кодированием, RLL - Run Limited Length, не использует импульсы синхронизации, применяется, в частности, в жестких дисках "винчестер'' и существует в нескольких разновидностях. Одна из них основана на замене тетрад байта на 5-битные группы. Эти группы подбираются таким образом, чтобы при передаче данных нули не встречались подряд более двух раз, что делает код самосинхронизирующимся. Например, тетрада 0000 заменяется группой бит 11001, тетрада 1000 - 11010, тетрада 0001 - 11011, тетрада 1111 - 01111 (См. рис. 7.5). Существуют разновидности RLL, в которых заменяются последовательности бит различной длины. Кодирование MFM или FM можно представить как частный случай RLL.
При необходимости передачи записанных с помощью некоторого кода сообщений по данному каналу приходиться преобразовывать эти сообщения в допустимые сигналы канала, т.е. производить надлежащее кодирование, а при приеме данных - декодирование. Кодирование целесообразно производить так, чтобы среднее время, затрачиваемое на передачу, было как можно меньше. Получается, что исходному входному алфавиту нужно однозначно сопоставить новый алфавит, обеспечивающий большую скорость передачи. В этом случае возникает явление задержки или запаздывания.
Поясним последнее на примере. Пусть источник сообщений посылает через
промежутки времени длиной 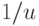 (т.е. со скоростью
(т.е. со скоростью  )
независимые символы
)
независимые символы  с вероятностями 1/2, 1/4, 1/8, 1/8, т.е., можно
сказать, что источник характеризуется некоторой д.с.в.
с вероятностями 1/2, 1/4, 1/8, 1/8, т.е., можно
сказать, что источник характеризуется некоторой д.с.в.  . Пусть канал -
без шумов. Символ либо передается по каналу, если тот свободен, либо ожидает (помещается
в память) до тех пор, пока канал не освободится. Выберем в качестве
кода для передачи символов источника по каналу следующий:
. Пусть канал -
без шумов. Символ либо передается по каналу, если тот свободен, либо ожидает (помещается
в память) до тех пор, пока канал не освободится. Выберем в качестве
кода для передачи символов источника по каналу следующий:  -00,
-00,  -01,
-01, 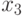 -10,
-10, 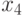 -11. Пусть
время, необходимое для передачи как
0, так и 1, равно
-11. Пусть
время, необходимое для передачи как
0, так и 1, равно  . Тогда если
. Тогда если  , то
за время между появлениями двух последовательных значений
, то
за время между появлениями двух последовательных значений  кодовое
значение успеет передаться и канал освобождается. Если же
кодовое
значение успеет передаться и канал освобождается. Если же 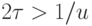 , то
, то  -й символ появится в момент
-й символ появится в момент  , а его кодовое обозначение будет передано
по каналу в момент
, а его кодовое обозначение будет передано
по каналу в момент 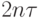 . Следовательно, промежуток времени между
появлением
. Следовательно, промежуток времени между
появлением  -го символа и моментом его получения равен
-го символа и моментом его получения равен  , т.е. этот
промежуток стремится к бесконечности при
, т.е. этот
промежуток стремится к бесконечности при 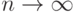 и передача
будет вестись с неограниченным запаздыванием. Выбором более удачного кода (например,
Хаффмена) можно увеличить скорость передачи.
и передача
будет вестись с неограниченным запаздыванием. Выбором более удачного кода (например,
Хаффмена) можно увеличить скорость передачи.
Следующий, основной факт теории передачи информации или основная теорема о кодировании при наличии помех позволяет при знании емкости канала и энтропии передатчика вычислить максимальную скорость передачи данных в канале.
Теорема Шеннона. Пусть источник характеризуется д.с.в.  .
Рассматривается канал с шумом, т.е. для каждого передаваемого
сообщения задана вероятность
.
Рассматривается канал с шумом, т.е. для каждого передаваемого
сообщения задана вероятность  его
искажения в процессе передачи (вероятность ошибки).
Тогда существует такая скорость передачи
его
искажения в процессе передачи (вероятность ошибки).
Тогда существует такая скорость передачи  ,
зависящая только от
,
зависящая только от  , что
, что  сколь угодно близкая к
сколь угодно близкая к  такая, что существует способ передавать
значения
такая, что существует способ передавать
значения  со скоростью
со скоростью 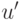 и с вероятностью ошибки меньшей
и с вероятностью ошибки меньшей  , причем
, причем

Кроме того, Фэно доказана120 следующая обратная теорема о кодировании при наличии помех. Для  можно найти такое положительное число
можно найти такое положительное число  , что в случае
передачи информации по линии связи со скоростью
, что в случае
передачи информации по линии связи со скоростью 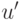 вероятность ошибки
вероятность ошибки  передачи каждого символа сообщения при любом методе
кодирования и декодирования будет не меньше
передачи каждого символа сообщения при любом методе
кодирования и декодирования будет не меньше  (
(  очевидно растет вслед за ростом
очевидно растет вслед за ростом 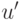 ).
).
Упражнение 33 По каналу связи без шума могут передаваться четыре сигнала длительностью 1 мс каждый. Вычислить емкость такого канала.
Упражнение 34 Три передатчика задаются случайными величинами со следующими законами распределениями вероятностей:
-
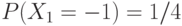 ,
, 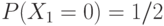 ,
, 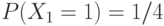 ;
; -
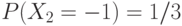 ,
, 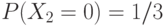 ,
,  ;
; 
Емкость канала связи с шумом равна 4000 бод. Вычислить максимальную скорость передачи данных по этому каналу каждым из передатчиков, обеспечивающую сколь угодно высокую надежность передачи.



