|
Здравствуйте прошла курсы на тему Алгоритмы С++. Но не пришел сертификат и не доступен.Где и как можно его скаачат? |
Потоки в сетях
Лемма 22.7. Количество расширяющих путей, необходимых в реализации алгоритма Форда-Фалкерсона с использованием кратчайших расширяющих путей, не превышает VE/2.
Доказательство. Сначала, как понятно из примера на рис. 22.17, ни один из кратчайших путей не короче предыдущего. Для доказательства этого факта мы покажем методом от противного, что справедливо еще более сильное свойство: никакой расширяющий путь не может уменьшить длину кратчайшего пути из вершины s в любую другую вершину остаточной сети. Предположим, что некоторый расширяющий путь может это сделать, а вершина v - первая вершина на таком пути. При этом возможны два случая: либо никакая вершина на новом более коротком пути из s в v не присутствует в этом расширяющем пути, либо некоторая вершина w на новом кратчайшем пути из s в v присутствует в расширяющем пути где-то между v и t. Обе ситуации противоречат условию минимальности расширяющего пути.
Теперь каждый расширяющий путь содержит, по построению, по крайней мере одно критическое ребро - ребро, которое удалено из остаточной сети, поскольку оно соответствует либо заполненному до пропускной способности прямому ребру, либо опустошенному обратному ребру. Предположим, что ребро u-v есть критическое ребро для расширяющего пути P длиной d. Следующий расширяющий путь, в котором это ребро также будет критическим, должен иметь длину не менее d + 2, т.к. он должен проходить из s до v, потом по ребру u-v, а затем из u в t. Первая часть имеет длину по крайней мере на 1 больше, чем расстояние от s до u в P, а последняя часть имеет длину по крайней мере на 1 больше, чем расстояние от v до t в P, поэтому длина этого пути по крайней мере на 2 больше, чем длина P. Поскольку длины расширяющих путей не могут быть больше V, то из этих фактов следует, что каждое ребро может быть критическим в не более чем V/2 расширяющих путях - значит, общее количество расширяющих путей не может быть больше EV/2. 
Следствие. Время, необходимое для отыскания максимального потока в разреженной сети, равно O(V3 ) .
Доказательство. Время, необходимое для отыскания расширяющего пути, равно O(E ), поэтому общее время равно
O(EV2 )
. Отсюда следует указанная граница. 
Величина V3 достаточно велика и поэтому не может гарантировать высокую производительность на крупных сетях. Но это не должно удерживать нас от применения алгоритма на крупных сетях, т.к. полученная оценка производительности в худшем случае вряд ли будет полезной для прогнозирования производительности алгоритма в практических ситуациях. Например, как было сказано выше, максимальная пропускная способность M (или максимальное отношение пропускных способностей) может быть намного меньше V, и тогда лемма 22.6 определяет более точную границу. Вообще-то в лучшем случае количество расширяющих путей, необходимых для метода Форда-Фалкерсона, меньше степени выхода вершины s или степени захода вершины t, которые, в свою очередь, могут быть намного меньше V. При таком разбросе производительности в лучшем и худшем случаях не стоит сравнивать алгоритмы нахождения расширяющих путей только на основе границ для худшего случая.
Однако существуют другие реализации, которые почти столь же просты, как и метод использования кратчайших расширяющих путей, но имеют более точные границы или хорошо зарекомендовали себя на практике (или и то, и другое). Допустим, в примере, представленном на рис. 22.17 и рис. 22.18, алгоритм с использованием максимального расширяющего пути использует намного меньше путей для отыскания максимального потока, чем метод с использованием кратчайшего расширяющего пути. Теперь мы проведем анализ худшего случая для рассматриваемого алгоритма.
Во-первых, как и в случае алгоритма Прима и алгоритма Дейкстры (см. "Минимальные остовные деревья" и рис. 21.2), мы можем реализовать очередь с приоритетами таким образом, что для выполнения одной итерации алгоритма в худшем случае понадобится время, пропорциональное V2 (для насыщенных графов) или (E+ V) logV (для разреженных графов). Однако эти оценки слишком пессимистичны, т.к. алгоритм сразу же останавливается при достижении стока. Мы также знаем, что можно немного повысить производительность, воспользовавшись специальными структурами данных. Однако более важной, хотя и более трудной, задачей является определение необходимого количества расширяющих путей.
Лемма 22.8. Количество расширяющих путей, необходимых в реализации алгоритма Форда-Фалкерсона с использованием максимальных расширяющих путей, не превышает 2E lgM.
Доказательство. Пусть дана некоторая сеть с максимальным потоком F. Пусть  - значение потока в некоторый момент выполнения алгоритма, перед поиском расширяющего пути. Применение леммы 22.2 к остаточной сети позволяет разложить поток на максимум E ориентированных путей, что дает в сумме
- значение потока в некоторый момент выполнения алгоритма, перед поиском расширяющего пути. Применение леммы 22.2 к остаточной сети позволяет разложить поток на максимум E ориентированных путей, что дает в сумме 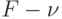 , поэтому поток по крайней мере в одном из путей равен не менее
, поэтому поток по крайней мере в одном из путей равен не менее 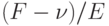 . Теперь либо мы найдем максимальный поток до использования следующих 2E расширяющих путей, либо величина расширяющего пути после использования этой последовательности 2E путей станет меньше
. Теперь либо мы найдем максимальный поток до использования следующих 2E расширяющих путей, либо величина расширяющего пути после использования этой последовательности 2E путей станет меньше 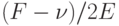 , а это меньше половины максимума до использования последовательности 2E путей. То есть для уменьшения мощности пути в два раза в худшем случае нужна последовательность из 2E путей. Первое значение количества путей не превышает M, которое придется уменьшать в два раза максимум lgM раз, что дает в конечном итоге максимум lgM последовательностей из 2E путей.
, а это меньше половины максимума до использования последовательности 2E путей. То есть для уменьшения мощности пути в два раза в худшем случае нужна последовательность из 2E путей. Первое значение количества путей не превышает M, которое придется уменьшать в два раза максимум lgM раз, что дает в конечном итоге максимум lgM последовательностей из 2E путей. 
Следствие. Время, необходимое для вычисления максимального потока в разреженной сети, составляет O(V2 lgM lgV) .
Доказательство. Это утверждение непосредственно следует из использования реализации очереди с приоритетами на основе пирамидального дерева, как при доказательстве лемм 20.7 и 21.5. 
Для значений M и V, которые обычно встречаются на практике, эта граница значительно ниже границы O(V3) , определяемой леммой 22.7. Во многих практических ситуациях алгоритм поиска максимального расширяющего пути использует значительно меньше итераций, чем алгоритм поиска кратчайшего расширяющего пути, за счет некоторого увеличения затрат на поиск каждого пути.
Можно рассмотреть и множество других вариантов, которые описаны в литературе по алгоритмам вычисления максимальных потоков. Продолжают появляться новые алгоритмы с более точными границами для худшего случая, однако существование нетривиальной нижней границы до сих пор не доказано, т.е. возможность открытия простого алгоритма с линейным временем выполнения остается. Многие алгоритмы разработаны в основном для снижения границ худшего случая для насыщенных графов, поэтому они не обеспечивают сущетвенно лучшую производительность по сравнению с алгоритмом поиска с использованием максимального расширяющего пути для различных видов разреженных сетей, с которыми мы сталкиваемся на практике. Однако остается еще много вариантов, которые могут привести к более эффективным практическим алгоритмам вычисления максимальных потоков. Ниже мы изучим еще два алгоритма расширения путей, а в разделе 22.3 рассмотрим другое семейство алгоритмов.
В одном простом алгоритме с помощью расширения путей используется значение уменьшающегося счетчика или стековая реализация для обобщенной очереди из программы 22.3 - при этом поиск расширяющих путей выполняется аналогично поиску в глубину. На рис. 22.20 показан поток, вычисленный этим алгоритмом для нашего небольшого примера. Интуитивно понятно, что этот метод быстро работает, легок в реализации и действительно находит максимальный поток. Как мы увидим, его производительность может быть всякой, от очень низкой для одних видов сетей до вполне приемлемой для других.
Здесь показано использование стека как основы для обобщенной очереди в нашей реализации метода Форда-Фалкерсона, когда поиск путей выполняется так же, как поиск в глубину. В этом случае рассматриваемый метод работает почти так же успешно, как и поиск в ширину, но его анализ не проводился - из-за несколько неустойчивого поведения и ощутимой зависимости от представления сети.
Другой альтернативой является использование в качестве обобщенной очереди реализации рандомизированной очереди, когда поиск расширяющего пути становится рандомизированным. На рис. 22.21 показан поток, вычисленный этим алгоритмом для нашего небольшого примера. Он также быстро работает и легок в реализации; а кроме того, как было сказано в "Поиск на графе" , он может сочетать в себе достоинства как поиска в ширину, так и поиска в глубину. Рандомизация - это мощный инструмент в разработке алгоритмов, и в данной ситуации она вполне уместна.
В завершение данного раздела мы еще ближе рассмотрим изученные методы, чтобы понять сложность их сравнения между собой или попыток прогнозирования производительности в практических ситуациях.
Чтобы получить начальное представление о возможных количественных различиях, мы воспользуемся двумя моделями транспортных сетей, построенных на основе модели евклидовых графов, которые мы уже применяли для сравнения других алгоритмов на графах. В обеих моделях используется граф из V точек на плоскости со случайными координатами от 0 до 1 и ребер, соединяющих точки, расположенные в пределах фиксированного расстояния друг от друга. Эти модели различаются пропускными способностями, назначаемыми ребрам.
Первая модель просто присваивает каждой пропускной способности одно и то же постоянное значение. Как будет показано в разделе 22.4, такая задача о сетевых потоках решается легче, чем общая задача. В рассматриваемых нами евклидовых графах потоки ограничены степенью выхода истока и степенью захода стока, поэтому в каждом алгоритме требуется найти лишь несколько расширяющих путей. Однако, как мы вскоре увидим, эти пути существенно различаются для разных алгоритмов.
Вторая модель назначает случайные пропускные способности из некоторого фиксированного диапазона значений. Эта модель генерирует типы сетей, которые люди обычно представляют себе при обдумывании задачи, а производительность различных алгоритмов на таких сетях дает богатую пищу для размышлений.
Здесь показан результат использования рандомизированной очереди для структуры данных накопителя при поиске расширяющих путей методом Форда-Фалкерсона. В этом примере мы случайно натолкнулись на короткий путь с высокой пропускной способностью, благодаря чему потребовалось относительно небольшое количество расширяющих путей. Хотя прогнозирование характеристик производительности этого метода представляет собой трудную задачу, во многих ситуациях он работает вполне хорошо.
Обе эти модели проиллюстрированы на рис. 22.22 - вместе с потоками, вычисленными четырьмя различными методами на двух сетях. Пожалуй, в этих примерах больше всего бросается в глаза существенное различие самих потоков. Все они имеют одну и ту же величину, но в рассматриваемых сетях имеется много максимальных потоков, и различные алгоритмы выбирают различные пути при их вычислении. Данная ситуация часто встречается на практике. Можно попытаться наложить дополнительные ограничения на вычисляемые потоки, но такие изменения в задаче усложняют ее решение. Задача отыскания потока минимальной стоимости, которую мы рассмотрим в разделах 22.5-22.7, представляет собой один из способов формализации подобных ситуаций.
В таблице 22.1 приведены более подробные количественные результаты относительно всех четырех методов вычисления потоков в сетях, показанных на рис. 22.22. Производительность алгоритма с использованием расширяющих путей зависит не только от количества расширяющих путей, но и от длины таких путей и затрат на их поиск. В частности, время выполнения пропорционально количеству ребер, просмотренных во внутреннем цикле программы 22.3. Как обычно, это количество может меняться в широких пределах - даже для одного и того же графа - и зависит от свойств его представления, но для каждого вида алгоритма все-таки имеются общие характеристики. Например, на рис. 22.23 и 22.24 показаны деревья поиска, соответственно, для алгоритма с использованием путей максимальной пропускной способности и алгоритма с использованием кратчайшего пути. Эти примеры подтверждают общий вывод, что метод поиска кратчайшего пути более трудоемок при отыскании расширяющих путей с меньшим потоком, чем алгоритм с использованием максимальной пропускной способности, и помогают понять, почему предпочтение отдается последнему.
В этой таблице представлены параметры производительности различных алгоритмов вычисления сетевых потоков с помощью расширения путей на примере евклидовой сети с соседними связями (со случайными значениями пропускной способности и с величиной максимального потока, равной 286) и с единичными пропускными способностями (при величине максимального потока, равной 1). Алгоритм использования путей с максимальной пропускной способностью превосходит другие алгоритмы на обоих типах сетей. Алгоритм со случайным поиском находит расширяющие пути, которые ненамного длиннее кратчайшего пути, и проверяет меньшее количество узлов. Алгоритм на основе стека очень хорошо работает для случайных весов. Хотя он находит очень длинные пути, он вполне пригоден для работы на сетях с единичными весами.
| Количество путей | Средняя длина | Общее количество ребер | |
|---|---|---|---|
| Случайные пропускные способности от 1 до 50 | |||
| Кратчайшие пути | 37 | 10,8 | 76394 |
| С максимальной пропускной способностью | 7 | 19,3 | 15660 |
| Поиск в глубину | 286 | 123,5 | 631392 |
| Случайный выбор | 35 | 12,8 | 58016 |
| Пропускная способность, равная 1 | |||
| Кратчайшие пути | 6 | 10,5 | 13877 |
| С максимальной пропускной способностью | 6 | 14,7 | 10736 |
| Поиск в глубину | 6 | 110,8 | 12291 |
| Случайный выбор | 6 | 12,2 | 11223 |
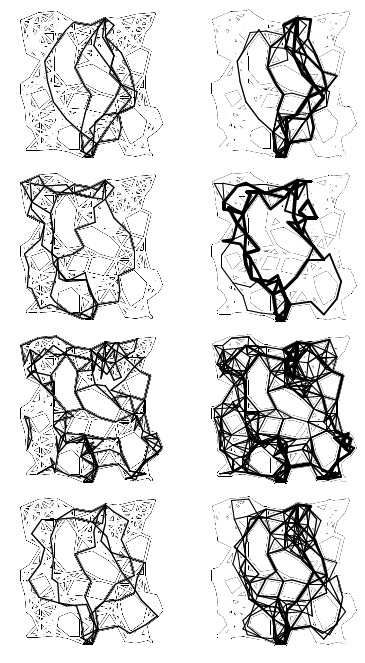
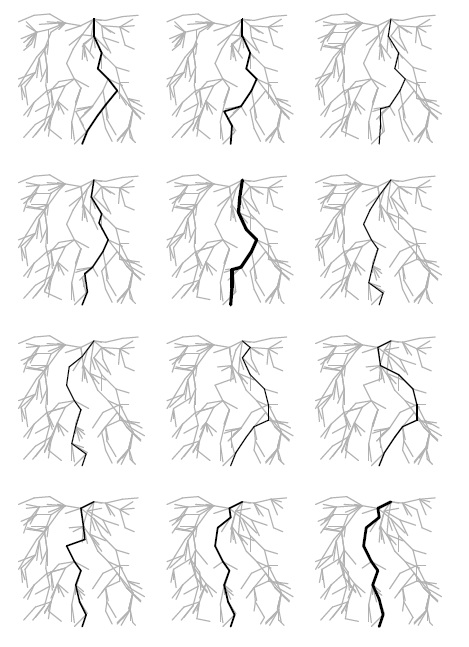
Здесь представлены вычисления максимальных потоков в случайных евклидовых графах, построенных на базе двух различных моделей пропускных способностей. Слева всем ребрам присвоена единичная пропускная способность, а справа - случайные пропускные способности. Исток находится в середине верхней части сети, а сток - в середине нижней части. На диаграммах показаны направленные сверху вниз потоки, которые вычислены с помощью алгоритма, использующего соответственно кратчайшие пути, пути с максимальной пропускной способностью, стек и рандомизированный выбор. Поскольку вершины не имеют высоких степеней, а пропускные способности принимают малые целочисленные значения, для этих примеров существует много различных потоков, которые приводят к максимальному.
Степень захода стока равна 6, поэтому все алгоритмы вычисляют поток в модели с единичными пропускными способностями (слева) с помощью шести расширяющих путей. Методы находят расширяющие пути, поведение которых существенно отличается от модели со случайными весами, представленной в правой части. В частности, метод с использованием стека находит длинные пути с малым весом и даже приводит к появлению потока с разорванным циклом.
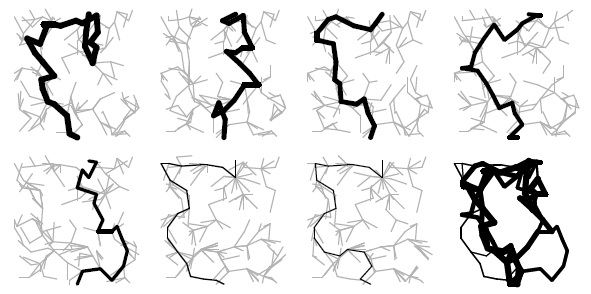
На этом рисунке показаны расширяющие пути, вычисленные алгоритмом с использованием путей максимальной пропускной способности для евклидовой сети со случайными весами, которая изображена на рис. 22.22 рис. 22.22. Здесь же показаны (серым цветом) ребра остовного дерева поиска на графе. Полученный поток показан внизу справа.
Пожалуй, основной урок, который можно вынести из подробного исследования конкретных сетей, состоит в огромной разнице между оценками верхней границы, которые даны в леммах 22.6-22.8, и фактическим количеством расширяющих путей, которые требуются алгоритмам в реальных приложениях. Например, в транспортной сети, представленной на рис. 22.23, имеется 177 вершин и 2000 ребер с пропускной способностью не более 100 единиц. Поэтому значение 2E lgM в лемме 22.8 больше 25000, но алгоритм с использованием путей с максимальной пропускной способностью находит максимальный поток, перебрав лишь семь расширяющих путей. Аналогично, значение VE/2 для этой сети, определяемое в лемме 22.7, равно 177000, однако алгоритму с использованием кратчайших путей достаточно перебрать лишь 37 путей.
Как уже было сказано, эти различия между теоретической и реальной производительностью в данном случае объясняются относительно низкими степенями узлов и локальностью связей. Можно вывести более точные границы производительности, учитывающие эти детали, однако такие различия между моделями транспортных сетей и реальными сетями являются правилом, а не исключением. С одной стороны, эти результаты можно считать свидетельством недостаточно общего характера сетей, которые встречаются на практике; но с другой стороны, видимо, анализ худших случаев еще более удален от практики, чем все эти виды сетей.
Подобные значительные расхождения побуждают исследователей искать более низкие границы для худших случаев. Существует множество других еще не исследованных возможных реализаций алгоритмов, использующих расширение путей, которые могут привести к более заметному повышению производительности в худшем случае или на реальных сетях, чем рассмотренные нами методы (см. упражнения 22.56-22.60). В специальной литературе приведены многочисленные более сложные методы, с улучшенной производительностью в худшем случае (см. раздел ссылок).
На этом рисунке показаны расширяющие пути, вычисленные алгоритмом с использованием кратчайших путей для евклидовой сети со случайными весами, которая изображена на рис. 22.22. Здесь же показаны (серым цветом) ребра остовного дерева поиска на графе. В этом случае алгоритм работает гораздо медленнее, чем алгоритм с использованием путей максимальной пропускной способности (см. рис. 22.23), т.к. он требует больше расширяющих путей (здесь показаны лишь первые 12 путей из всех 37, а остовные деревья имеют больший размер (обычно содержат почти все вершины).
При изучении множества других задач, сводящихся к задаче о максимальном потоке, может возникнуть важное осложнение. Полученные в результате сведения транспортные сети могут иметь специальную структуру, которой могут воспользоваться специализированные алгоритмы для повышения производительности. Например, в разделе 22.8 мы рассмотрим сведение, которое дает транспортную сеть с единичными пропускными способностями всех ребер.
Даже если ограничиться только алгоритмами с использованием расширения путей, мы увидим, что изучение алгоритмов вычисления максимального потока - это и наука, и искусство. Искусство проявляется в выборе стратегии, наиболее эффективной в данной практической ситуации, а наука - в понимании природы задачи. Существуют ли новые структуры данных и алгоритмы, которые могут решить задачу вычисления максимального потока за линейное время, либо можно доказать, что такое решение не существует? В разделе 22.3 будет показано, что никакой алгоритм с использованием расширения путей не может иметь линейную производительность в худшем случае; там же мы рассмотрим другое обобщенное семейство алгоритмов, которые могут это сделать.
Упражнения
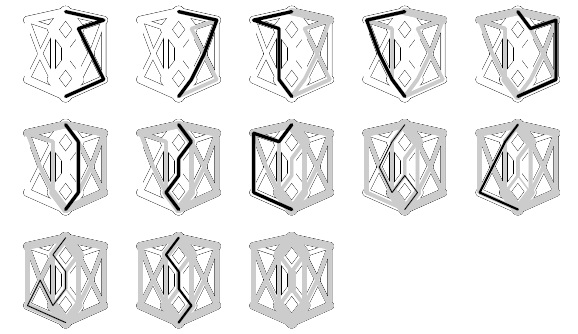
22.19. Покажите в стиле рис. 22.13 столько различных последовательностей расширяющих путей, сколько вы их сможете найти в транспортной сети, показанной на рис. 22.10
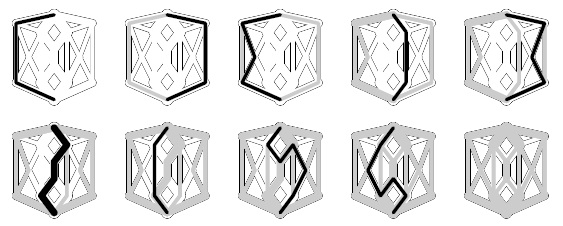
22.20. Покажите в стиле рис. 22.15 все сечения транспортной сети, показанной на рис. 22.10, их секущие множества и пропускные способности.
22.21. Найдите минимальное сечение в транспортной сети, показанной на рис. 22.11.
22.22. Допустим, в некоторой транспортной сети достигнут баланс пропускных способностей (для каждого внутреннего узла общая пропускная способность входящих ребер равна общей пропускной способности исходящих ребер). Использует ли алгоритм Форда-Фалкерсона обратные ребра? Докажите, что использует, либо приведите контрпример.
22.23. Определите максимальный поток для транспортной сети с рис. 22.5, в которой величина по крайней одного потока не является целым числом.
22.24. Разработайте реализацию алгоритма Форда-Фалкерсона, в которой вместо очереди с приоритетами используется обобщенная очередь (см. "Поиск на графе" ).
22.25. Докажите, что количество расширяющих путей, необходимых для любой реализации алгоритма Форда-Фалкерсона, не более чем в V раз больше наименьшего целого числа, которое больше отношения наибольшей пропускной способности ребра к наименьшей пропускной способности.
22.26. Докажите справедливость нижней границы линейного времени для задачи поиска максимального потока: покажите, что в сети с любыми значениями V и E любой алгоритм вычисления максимального потока должен просмотреть каждое ребро.
22.27. Приведите пример сети наподобие рис. 22.19, для которой алгоритм с использованием кратчайших расширяющих путей обладает наихудшим поведением, как на рис. 22.19.
22.28. Приведите представление списками смежности для сети, изображенной на рис. 22.19, для которой наша реализация поиска с помощью стека (программа 22.3, в которой в качестве обобщенной очереди используется стек) обладает наихудшим поведением.
22.29. Покажите в стиле рис. 22.16 транспортную и остаточную сети после каждого расширения пути, когда алгоритм с использованием кратчайших расширяющих путей отыскивает максимальный поток в транспортной сети с рис. 22.10. Включите также деревья поиска на графе для каждого расширяющего пути. Если можно выбрать более одного пути, покажите тот, который выбирается реализациями, рассмотренными в этом разделе.
22.30. Выполните упражнение 22.29 для алгоритма с использованием расширяющего пути с максимальной пропускной способностью.
22.31. Выполните упражнение 22.29 для алгоритма с выборкой расширяющего пути из стека.
22.32. Приведите семейство сетей, для которых алгоритм с использованием максимального расширяющего пути перебирает 2E lgM расширяющих путей.
22.33. Можно ли так упорядочить ребра, чтобы рассмотренные нами реализации тратили на поиск пути в упражнении 22.32 время, пропорциональное E? При необходимости измените пример, чтобы достичь этой цели. Опишите представление графа списками смежности, построенное для рассматриваемого примера. Объясните, как можно получить наихудший случай.
22.34. Эмпирически определите количество расширяющих путей и отношения времени выполнения к V для каждого из четырех алгоритмов, описанных в этом разделе, для различных видов сетей (см. упражнения 22.7-22.12).
22.35. Разработайте и протестируйте реализацию метода расширения путей, который использует эвристику кратчайшего пути из истока в сток для евклидовых сетей из "Кратчайшие пути" .
22.36. Разработайте и протестируйте реализацию метода расширения путей, основанного на чередующемся росте деревьев поиска с корнями в истоке и стоке (см. упражнения 21.35 и 21.75).
22.37. Реализация программы 22.3 останавливает поиск на графе, как только находит первый расширяющий путь из истока в сток, расширяет поток, а затем начинает поиск с самого начала. Другой способ - продолжить поиск и найти другой путь, пока не будут помечены все вершины. Разработайте и протестируйте второй подход.
22.38. Разработайте и протестируйте метод расширения путей, который использует не простые пути.
22.39. Приведите последовательность простых расширяющих путей, которые создают поток с циклом в сети, показанной на рис. 22.11.
22.40. Приведите пример, показывающий, что не все максимальные потоки можно получить расширением потоков вдоль некоторой последовательности простых путей из истока в сток, начиная с пустой сети.
22.41.[ Габов] Разработайте реализацию вычисления максимального потока, которая использует m = lgM этапов, где i-й этап решает задачу о максимальном потоке, используя i первых разрядов в значениях пропускных способностей. Начните с нулевого потока во всей сети; после первого этапа увеличьте вдвое поток, вычисленный на предыдущем этапе. Эмпирически сравните этот метод с базовыми методами на различных сетях (см. упражнения 22.7-22.12).
22.42. Докажите, что время выполнения алгоритма, описанного в упражнении 22.41, равно O(VE lgM).
22.43. Поработайте с гибридными методами, которые вначале используют один метод расширения путей, а затем переключаются на другой метод расширения путей до завершения работы (часть задачи - выбор подходящего критерия для определения момента переключения). Эмпирически сравните этот метод с базовыми методами на различных сетях (см. упражнения 22.7-22.12), обращая больше внимания на те, которые показывают лучшие результаты.
22.44. Поработайте с гибридными методами, которые попеременно используют два или более различных методов расширения путей. Эмпирически сравните этот метод с базовыми методами на различных сетях (см. упражнения 22.7-22.12), обращая больше внимания на те, которые показывают лучшие результаты.
22.45. Поработайте с гибридными методами, которые случайным образом переключаются между двумя или более различными методами расширения путей. Эмпирически сравните этот метод с базовыми методами на различных сетях (см. упражнения 22.7-22.12), обращая больше внимания на те, которые показывают лучшие результаты.
22.46. Напишите клиентскую функцию для транспортной сети, которая для заданного целого числа с находит ребро, увеличение пропускной способности которого в с раз увеличивает максимальный поток до максимальной величины. Эта функция может считать, что клиент уже вычислил максимальный поток с помощью функции MAXFLOW.
22.47. Пусть задано минимальное сечение некоторой сети. Облегчает ли эта информация вычисление максимального потока? Разработайте алгоритм, который использует заданное минимальное сечение для существенного ускорения поиска расширяющих путей с максимальными пропускными способностями.
22.48. Напишите клиентскую программу для графической анимации динамики алгоритмов поиска расширяющих путей. Эта программа должна создавать изображения, подобные рис. 22.17 и другим рисункам из этого раздела (см. упражнения 17.55-17.59). Протестируйте полученную реализацию на евклидовых сетях из упражнений 22.7-22.12.