|
Здравствуйте прошла курсы на тему Алгоритмы С++. Но не пришел сертификат и не доступен.Где и как можно его скаачат? |
Потоки в сетях
Транспортные сети
Наше описание алгоритмов вычисления сетевых потоков мы начнем с идеализированной физической модели, которая наглядно продемонстрирует несколько фундаментальных понятий. Допустим, что имеется система взаимосвязанных нефтепроводных труб различных диаметров, а на соединениях труб установлены вентили, управляющие движением потоков, как показано на рис. 22.5. Далее мы будем предполагать, что в системе трубопроводов имеется единственный исток (допустим, нефтяное месторождение) и единственный сток (к примеру, нефтеперерабатывающий завод), в который попадают все потоки. В каждом соединении потоки нефти находятся в равновесии: объем поступающей нефти равен объему вытекающей нефти. Мы будем измерять потоки и пропускную способность труб в одних и тех же единицах (например, в галлонах в секунду).
Если общая пропускная способность труб, входящих в каждый вентиль, равна общей пропускной способности выходящих труб, то решать вообще нечего: нужно просто заполнить по максимуму все трубы. Иначе будут заполнены не все трубы, но нефть будет течь по трубам в соответствии с настройками вентилей и свойством, что объем нефти, поступающей в каждое соединение, равен объему вытекающей нефти. А из баланса в соединениях следует и общий баланс в сети: в лемме 22.1 будет показано, что объем нефти, втекающей в сток, равен объему нефти, вытекающей из истока. А, как показано на рис. 22.6, настройки вентилей на соединениях могут оказывать нетривиальное влияние на потоки в сети. И вот нас интересует следующий вопрос: какие настройки вентилей обеспечат максимальный поток нефти из истока в сток?
Эту ситуацию можно непосредственно смоделировать при помощи сети (взвешенный орграф, согласно определению из "Кратчайшие пути" ) с одним истоком и одним стоком. Ребра сети соответствуют трубам, вершины соответствуют соединениям труб с вентилями, которые регулируют потоки нефти в исходящие ребра, а веса ребер соответствуют пропускной способности труб. Мы считаем ребра ориентированными, т.е. нефть в каждой трубе может течь только в одном направлении. По каждой трубе проходит определенный поток, который меньше или равен ее пропускной способности, и каждая вершина удовлетворяет условию баланса: входной поток равен выходному потоку.
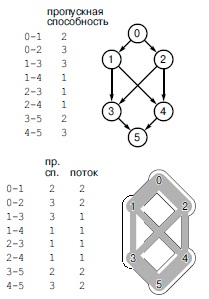
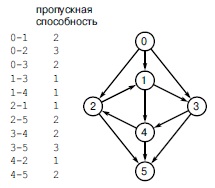
Транспортная сеть - это взвешенная сеть, в которой веса ребер интерпретируются как пропускные способности (вверху). Требуется вычислить второе множество весов ребер, ограниченное пропускными способностями, которые мы называем потоками. Внизу показаны наши соглашения относительно вычерчивания транспортных сетей. Ширина каждого ребра пропорциональна его пропускной способности; объем потока в каждом ребре показан заштрихованной частью; поток на наших рисунках всегда направлен из единственного истока вверху в единственный сток внизу; пересечения (как между ребрами 1-4 и 2-3 в рассматриваемом примере) не представляют вершин, если не обозначены как вершины. За исключением истока и стока, в каждой вершине входной поток равен выходному потоку: например, в вершину 2 входят 2 единицы потока (из вершины 0) и выходят 2 единицы потока (1 единица в вершину 3 и 1 единица в вершину 4).
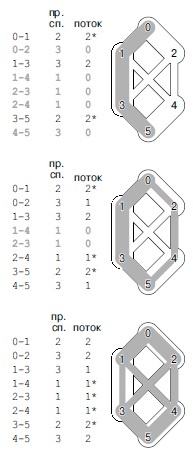
Открыв вентили вдоль пути 0-1-3-5, можно инициировать в этой сети поток мощностью 2 единицы (вверху); открыв вентили вдоль пути 0-2-4-5, получим еще 1 единицу потока (в центре). Звездочками отмечены заполненные ребра. Поскольку ребра 0-1, 2-4 и 3-5 заполнены, прямого способа увеличить поток из 0 в 5 не существует, но если еще открыть вентиль в вершине 1, чтобы направить часть потока в ребро 1-4 , то будет задействовано ребро 4-5, благодаря чему будет получен максимальный поток в данной сети (внизу).
Такая абстракция транспортной сети представляет собой полезную модель решения задач, которая непосредственно применима к широкому кругу ситуаций, а косвенно - к еще более широкому кругу. Иногда для наглядности мы представляем нефть, текущую по нефтепроводу, но можно представлять и товары, перемещаемые по каналам распределения, и другие ситуации.
Потоковая модель непосредственно применима к задаче распределения - при этом значения потоков интерпретируются как их интенсивность, и транспортная сеть описывает потоки товаров точно так же, как и потоки нефти. Например, потоки на рис. 22.5 можно интерпретировать так: два элемента в единицу времени пересылаются из вершины 0 в 1 и из 0 в 2, один элемент в единицу времени - из 0 в 2, один элемент в единицу времени - из 1 в 3 и из 1 в 4 и т.д.
Другой способ интерпретации потоковой модели для задачи распределения - потоки интерпретируются как объемы товаров, и тогда сеть описывает только одноразовую рассылку товара. Например, потоки на рис. 22.5 можно интерпретировать, как трехэтапную поставку четырех единиц товара из вершины 0 в 5: сначала пересылаются две единицы товара из 0 в 1 и две единицы из 0 в 2, так что в каждой из этих вершин остается по две единицы товара. Далее выполняется пересылка по одной единице товара из 1 в 3, из 1 в 4 , из 2 в 3 и из 2 в 4 , и в каждой из вершин 3 и 4 остается по две единицы товара. Рассылка завершается доставкой двух единиц товара из вершины 3 в 5 и двух единиц из 4 в 5.
Как и в случае использования расстояния в алгоритмах поиска кратчайшего пути, мы вполне можем, когда это удобно, отказаться от любой физической интерпретации, т.к. все рассматриваемые нами определения, леммы и алгоритмы основаны исключительно на абстрактной модели, которая не обязана подчиняться физическим законам. Вообще-то основная причина нашего интереса к модели сетевых потоков в том, что она позволяет решать методом сведения множество других задач - в этом мы убедимся в разделах 22.4 и 22.6. В силу такой универсальности целесообразно дать точные определения терминов и понятий, с которыми мы ознакомились неформально.
Определение 22.1. Сеть с вершиной s, выбранной в качестве истока, и с вершиной t, выбранной в качестве стока, называется st-сетью.
В этом определении слово " выбранный " означает, что вершина s не обязательно должна быть истоком (вершина без входящих ребер), а вершина t - стоком (вершина без исходящих ребер), но мы будем рассматривать их именно так, игнорируя в наших рассуждениях (и алгоритмах) ребра, входящие в s, и ребра, исходящие из t. Во избежание путаницы в наших примерах мы будем рассматривать сети с одним истоком и стоком, а более общие ситуации рассмотрим в разделе 22.4. Вершины s и t мы будем называть, соответственно, " истоком " и " стоком " st-сети, поскольку они выполняют в сети именно эти роли. Остальные вершины сети мы будем называть внутренними вершинами.
Определение 22.2. Транспортная сеть (flow network) - это st-сеть с положительными весами ребер, которые мы будем называть пропускными способностями (capacity). Поток (flow) в транспортной сети - это множество неотрицательных весов ребер, которые называются реберными потоками (edge flow) и удовлетворяют условиям: поток в любом ребре не превышает пропускную способность этого ребра, а суммарный поток, входящий в каждую внутреннюю вершину, равен суммарному потоку, выходящему из этой вершины.
Мы будем называть суммарный поток в вершину притоком (inflow) этой вершины, а суммарный поток из вершины - оттоком (outflow) этой вершины. По соглашению потоки в ребрах, входящих в исток, и потоки в ребрах, исходящих из стока, равны нулю, а в лемме 22.1 будет показано, что отток истока всегда равен притоку стока, и этот поток мы будем называть мощностью (value) сети. Имея эти определения, нетрудно дать формальное определение нашей основной задачи.
Максимальный поток. Для заданной st-сети необходимо найти такой поток, что никакой другой поток из s в t не имеет большего значения. Для краткости будем называть такой поток максимальным потоком (maxflow), а задачу вычисления такого потока в сети будем называть задачей о максимальном потоке. В некоторых приложениях достаточно знать только величину максимального потока, но обычно требуется знать структуру потока (величины каждого реберного потока), обеспечивающего эту величину.
На ум тут же приходят различные варианты этой задачи. Можно ли рассматривать сеть с несколькими истоками и стоками? А как насчет сетей без истоков и стоков? Может ли поток проходить по ребрам в обоих направлениях? Возможны ли ограничения на пропускную способность вершин вместо ограничений на ребра (или наряду с ними)? Для алгоритмов на графах характерно то, что отделение тривиальных ограничений от ограничений, влекущих далеко идущие последствия, само по себе может оказаться трудной задачей. После того, как мы рассмотрим алгоритмы решения фундаментальной задачи, в разделах 22.2 и 22.3 мы исследуем эту задачу и приведем примеры сведения к задаче о максимальном потоке множества других с виду различных задач.
Характерным свойством потоков является условие локального баланса: в каждой внутренней вершине приток равен оттоку. На пропускные способности ребер такое ограничение не накладывается, и вообще-то именно нарушение баланса между суммарной пропускной способностью входящих ребер и суммарной пропускной способностью исходящих ребер и характеризует задачу о максимальном потоке. Условие баланса должно выполняться в каждой внутренней вершине, но оказывается, что это локальное свойство определяет и глобальное перемещение по сети. Однако пока это гипотеза, которую еще нужно доказать.
Лемма 22.1. Любой st-поток обладает тем свойством, что отток из вершины s равно притоку в вершину t.
Доказательство. (Термин st-поток (st-flow), означает " поток в st-сети " .) Добавим в сеть ребро из фиктивной вершины в вершину s, с потоком и пропускной способностью, равными оттоку вершины s, и ребро из вершины t в другую фиктивную вершину, с потоком и пропускной способностью, равными притоку вершины t. Теперь по индукции можно доказать более общее свойство: приток равен оттоку для любого множества вершин (без фиктивных вершин).
По условию локального баланса это свойство верно для любой одиночной вершины. Предположим теперь, что это свойство выполняется для некоторого множества вершин S, и добавим в это множество одиночную вершину v - получим множество S' = S U {v}. При вычислении притока и оттока для S' обратим внимание на то, что каждое ребро, ведущее из вершины v в некоторую вершину из S, уменьшает отток (из вершины v) на ту же величину, на какую оно уменьшает приток (в S); каждое ребро, ведущее в v из некоторой вершины множества S, уменьшает приток (в вершину v) на ту же величину, на какую уменьшает отток (из S); все другие ребра обеспечивают приток или отток для множества S' тогда и только тогда, когда они делают это для S или для v. Таким образом, для S' приток равен оттоку, а величина потока равна сумме величин потоков S и v, минус сумма потоков в ребрах, соединяющих v с вершинами из S (в любом направлении).
Применяя это свойство к множеству всех вершин сети, получим, что приток в исток из связанной с ней фиктивной вершины (который равен оттоку истока) равен оттоку из стока в связанную с ним фиктивную вершину (который равен притоку стока). 
Следствие. Величина потока объединения двух множеств вершин равна сумме величин каждого из потоков этих двух множеств минус сумма весов ребер, соединяющих вершину одного множества с вершиной другого множества.
Доказательство. Приведенное выше доказательство для множества S и вершины v работает и в том случае, когда мы заменяем вершину v некоторым множеством T (которое не пересекается с S). Иллюстрация этой леммы приведена на
рис.
22.7. 
В доказательстве леммы 22.1 можно обойтись и без фиктивных вершин, добавить в любую транспортную сеть ребро из t в s с пропускной способностью, равной мощности сети, и знать, что приток равен оттоку для любого множества узлов этой расширенной сети. Такой поток называется циркуляцией (circulation), а подобное построение показывает, что задача о максимальном потоке сводится к задаче поиска такой циркуляции, которая обеспечивает максимальный поток в заданном ребре.
Это иллюстрация сохранения баланса потоков при объединении множеств вершин. Два меньших овала соответствуют двум произвольным непересекающимся множествам вершин, а буквы представляют потоки в множествах ребер: A - величина потока в левое множество, кроме притока из правого множества, х - величина потока в левое множество из правого множества и т.д. Если имеет место баланс потоков между двумя множествами, то должно выполняться равенство A + x = B + у для левого множества и C + y = D + x для правого множества. Суммируя эти два равенства и исключая сумму x + у, мы получим A + C = B + D, - т.е. для объединения двух множеств приток равен оттоку.
В некоторых ситуациях подобная формулировка упрощает наши рассуждения. Например, как показано на рис. 22.8, она приводит к интересному альтернативному представлению потоков как множества циклов.
Если задано множество циклов и величина потока для каждого цикла, то легко вычислить соответствующую циркуляцию: нужно пройти по каждому циклу и добавить указанную величину потока к каждому ребру. Обратное свойство более интересно: можно найти множество циклов (и величину потока для каждого из них), которое эквивалентно любой заданной циркуляции.
Лемма 22.2. (Теорема разложения потока). Любую циркуляцию можно представить в виде потока в некотором множестве из не более чем E направленных циклов.
Доказательство. Этот результат можно получить с помощью простого алгоритма: будем повторять следующий процесс, пока имеются ребра, по которым проходят потоки. Начнем с произвольного ребра с ненулевым потоком, пройдем по любому ребру с ненулевым потоком, исходящему из конечной вершины первого ребра, и продолжаем эту процедуру, пока не попадем в уже посещенную вершину (обнаружен цикл). Выполним обратный обход по обнаруженному циклу, найдем ребро с минимальным потоком, а затем уменьшим потоки в каждом ребре цикла на это значение. Каждое повторение этого процесса обнуляет поток по меньшей мере в одном ребре, поэтому в сети может быть не более E циклов. 
Процесс, описанный в доказательстве, показан на рис. 22.9. В случае st-потоков применение этой леммы к циркуляции, полученной добавлением ребра из s в t, позволяет сделать вывод, что любой st-поток можно представить в виде потока вдоль множества не более E ориентированных путей, каждый из которых есть либо путь из s в t, либо цикл.
Следствие. Для максимального потока любой st-сети подграф, индуцированный ненулевыми потоками, является ациклическим.
Доказательство. Циклы, не содержащие ребро t- s, не меняют величину потока, поэтому можно обнулить поток в любом таком цикле, не меняя величину общего потока. 
Следствие. Максимальный поток любой st-сети можно представить в виде потока вдоль множества не более чем E ориентированных путей из s в t.
Доказательство. Очевидно. 
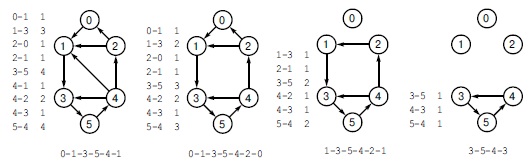
Здесь показано, что приведенную слева циркуляцию можно разложить на четыре цикла 1-3-5-4-1, 0-1-3-5-4-2-0, 1-3-5-4-2-1 и 3-5-4-3 с весами, соответственно, 2, 1, 1 и 3. Ребра каждого цикла показаны в соответствующем столбце, а суммирование весов каждого ребра в каждом цикле, в который оно входит (по соответствующей строке), дает его вес в циркуляции.
Чтобы разложить произвольную циркуляцию на множество циклов, мы многократно выполняем следующий процесс: проходим по любому пути, пока не встретим какой-либо узел второй раз, затем находим минимальный вес в обнаруженном цикле, после чего вычитаем минимальный вес из весов каждого ребра обнаруженного цикла и удаляем каждое ребро, вес которого стал нулевым. Например, на первой итерации мы проходим по пути 0-1-3-5-4-1 и обнаруживаем цикл 1-3-5-4-1, потом вычитаем 1 из весов всех ребер цикла, и в результате удаляем из цикла ребро 4-1, так как его вес стал нулевым. На второй итерации мы удаляем ребра 0-1 и 2-0, на третьей - 1-3, 4-2 и 2-1, а на последней итерации удаляем 3-5, 5-4 и 4-3.
Эти свойства позволяют получить представление о природе потоков, что будет полезно при разработке и анализе алгоритмов вычисления максимальных потоков.
С одной стороны, мы можем рассмотреть более общую формулировку задачи вычисления максимального потока в сети с несколькими истоками и стоками. Это позволит использовать наши алгоритмы для более широкого спектра приложений. С другой стороны, мы можем рассмотреть специальные случаи, например, ациклические сети. Это может облегчить решение задачи. Хотя, как мы убедимся в разделе 22.4, по трудности решения эти варианты эквивалентны рассматриваемой нами версии. Поэтому в первом случае мы можем приспособить наши алгоритмы и приложения для более широкой области приложений, а во втором случае вряд ли найдется более легкое решение. В приведенных здесь иллюстрациях мы используем ациклические графы, поскольку легче понять такие примеры, когда направление потока естественное - сверху вниз, но наши реализации допускают существование сетей с циклами.
Для реализации алгоритма вычисления максимального потока мы воспользуемся классом GRAPH из "Минимальные остовные деревья" , но с указателями на более сложный класс EDGE. Вместо одного веса, как это было в "Минимальные остовные деревья" и "Кратчайшие пути" , мы используем приватные члены данных pcap и pflow (пропускная способность и величина потока), а также общедоступные функции-элементы cap() и flow(), которые возвращают их значения. Хотя сети являются ориентированными графами, наши алгоритмы будут проходить по ребрам в обоих направлениях, поэтому мы используем представление в виде неориентированного графа из "Минимальные остовные деревья" и функцию-член from, которая позволяет отличить ребро u-v от ребра v-u .
Такой подход позволяет отделить абстракцию, необходимую нашим алгоритмам (ребра идут в обоих направлениях), от конкретной структуры клиентских данных и ставит перед этими алгоритмами простую цель: присвоить элементам flow в ребрах клиента такие значения, которые максимизируют поток через сеть. Критическим моментом наших реализаций является замена абстракции сети, которая зависит от значений потока и реализуется функциями-членами класса EDGE. Мы рассмотрим реализацию класса EDGE в разделе 22.2 (программа 22.2).
Поскольку транспортные сети обычно разрежены, мы воспользуемся классом GRAPH на основе представления списками смежных вершин, как в реализации класса SparceMultiGRAPH из программы 20.5. Но более важно то, что типичные транспортные сети могут содержать параллельные ребра (различной пропускной способности), соединяющие две вершины. Класс SparceMultiGRAPH не требует специальных мер в подобных ситуациях, но в случае представления графа матрицей смежности клиентам придется объединить такие ребра в одно ребро.
В представлениях сетей, описанных в "Минимальные остовные деревья" и 21, применялось соглашение, что веса представляются вещественными числами от 0 до 1. В этой главе мы полагаем, что веса (пропускные способности и величины потоков) представляют собой да-разрядные целые числа (от 0 до 2m - 1 ). Это сделано по двум основным причинам. Во-первых, нам часто придется проверять на равенство различные линейные комбинации весов, а в случае чисел с плавающей точкой это не всегда удобно. Во-вторых, время выполнения алгоритмов может зависеть от относительных значений весов, а параметр M = 2m удобен для ограничения значений весов. Например, отношение наибольшего веса к наименьшему ненулевому весу меньше M. Использование целочисленных весов - лишь один из многочисленных возможных вариантов (см., например, упражнение 20.8) при решении подобных задач.
Иногда удобно рассматривать ребра с неограниченной пропускной способностью, что означает, что мы не сравниваем поток с пропускной способностью такого ребра. В такой ситуации можно воспользоваться сигнальным значением с заведомо большим значением, чем величина любого потока.
Программа 22.1 представляет собой клиентскую функцию, которая проверяет, удовлетворяют ли потоки условию баланса в каждом узле, и если удовлетворяют, то возвращает значение мощности потока. Вызов этой функции можно включить в алгоритм вычисления максимального потока в качестве заключительной операции. Несмотря на все доверие к лемме 22.1, программистская осторожность требует также проверить, равен ли поток, вытекающий из истока, потоку, втекающему в сток. Иногда имеет смысл проверить, что ни в одном ребре поток не превосходит пропускную способность этого ребра и что структуры данных внутренне непротиворечивы (см. упражнение 22.12).
Программа 22.1. Проверка и вычисление мощности потока
Вызов flow(G, v) вычисляет разность между входным и выходным потоками в вершине v сети G. Вызов flow(G, s, t) проверяет величины сетевых потоков из истока (s) в сток (t). Если входной поток в некотором внутреннем узле не равен выходному потоку или если величина какого-либо потока меньше нуля, то возвращается 0; иначе возвращается величина потока.
template <class Graph, class Edge>
class check {
public:
static int flow(Graph &G, int v)
{ int x = 0; typename Graph::adjIterator A(G, v);
for (Edge* e = A.beg(); !A.end(); e = A.nxt())
x += e->from(v) ? e->flow() : -e->flow();
return x;
}
static bool flow(Graph &G, int s, int t)
{ for (int v = 0; v < G.V(); v++)
if ((v != s) && (v != t))
if (flow(G, v) != 0) return false;
int sflow = flow(G, s);
if (sflow < 0) return false;
if (sflow + flow(G, t) != 0) return false;
return true;
}
};
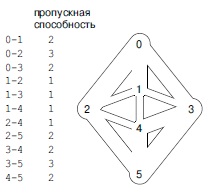
Эта транспортная сеть используется в нескольких упражнениях данной главы.
Данная транспортная сеть похожа на сеть, изображенной на рис. 22.10, только направления двух ребер заменены на обратные, вследствие чего появлились два цикла. Эта транспортная сеть также рассматривается в нескольких упражнениях данной главы.
Упражнения
22.1. Найдите два различных максимальных потока в транспортной сети, изображенной на рис. 22.10.
22.2. Пусть все пропускные способности выражаются положительными целыми числами, меньшими M. Каков максимально возможный поток для произвольной st-сети с V вершинами и E ребрами? Дайте два ответа, в зависимости от того, допускаются ли параллельные ребра.
22.3. Приведите алгоритм решения задачи о максимальном потоке для случая, когда сеть образует дерево, если удалить сток.
22.4. Приведите семейство сетей с E ребрами и циркуляцией, в которых процесс, описанный в доказательстве леммы 22.2, порождает E циклов.
22.5. Напишите класс EDGE, представляющий пропускные способности и потоки в виде вещественных чисел от 0 до 1 с d цифрами после десятичной точки, где d - фиксированная константа.
22.6. Напишите программу, которая строит транспортную сеть, считывая из стандартного ввода ребра (пары целых чисел в интервале от 0 до V- 1) с целочисленными пропускными способностями. Считайте, что верхняя граница пропускной способности M не превосходит 220.
22.7. Добавьте в решение упражнения 22.6, возможность присваивать вершинам символические имена, а не номера (см. программу 17.10).
22.8. Найдите в интернете крупную транспортную сеть, которую можно использовать для тестирования алгоритмов вычисления потоков. Это могут быть сети перевозки материалов (автомобильные, железнодорожные, авиа), сети связи (телефонные или компьютерные сети передачи данных) или распределительные сети. Если пропускные способности не известны, продумайте подходящую модель для их добавления. Напишите программу, использующую интерфейс программы 22.2 для реализации транспортных сетей с вашими данными - возможно, на основе решения упражнения 22.7. При необходимости разработайте дополнительные приватные функции для очистки данных (см. упражнения 17.33-17.35).
22.9. Напишите генератор случайных разреженных сетей с пропускными способностями от 0 до 220, взяв за основу программу 17.7. Воспользуйтесь отдельным классом для пропускных способностей и разработайте две реализации, одна из которых генерирует равномерно распределенные пропускные способности, а другая - нормально распределенные. Разработайте клиентские программы, которые генерируют случайные сети для обоих типов распределений весов с подобранными значениями V и E, чтобы использовать их для выполнения эмпирических тестов на графах, полученных из различных распределений весов ребер.
22.10. Напишите генератор случайных насыщенных сетей с пропускными способностями от 0 до 220, взяв за основу программу 17.8 и генераторы пропускных способностей ребер из упражнения 22.9. Напишите клиентские программы генерации случайных сетей для обоих распределений весов с подобранными значениями V и E, чтобы использовать их для выполнения эмпирических тестов на графах, полученных из этих моделей.
22.11. Напишите программу, которая генерирует на плоскости V случайных точек, затем строит транспортную сеть с (двунаправленными) ребрами, соединяющими все пары точек, расположенных на расстоянии не более d одна от другой (см. программу 3.20), и устанавливает пропускную способность каждого ребра с помощью одной из случайных моделей, описанных в упражнении 22.9. Определите, как выбрать d, чтобы ожидаемое количество ребер было равно E.
22.12. Добавьте в программу 22.1 проверку, что величина потока каждого ребра не больше его пропускной способности.
22.13. Найти все максимальные потоки в сети, показанной на рис. 22.11. Приведите представление циклами для каждого из них.
22.14. Напишите функцию, которая считывает величины потоков и циклы (по одному в строке, в формате, представленном на рис. 22.8) и строит сеть с соответствующим потоком.
22.15. Напишите клиентскую функцию, которая находит представление циклами для потока сети, используя метод, описанный в доказательстве леммы 22.2, и выводит величины потоков и циклы (по одному в строке, в формате, представленном на рис. 22.8).
22.16. Напишите функцию, которая удаляет циклы из st-потока сети.
22.17. Напишите программу, которая назначает целочисленные потоки каждому ребру в любом заданном орграфе без истоков и стоков, чтобы получилась транспортная сеть, представляющая собой циркуляцию.
22.18. Пусть поток представляет собой товары, которые перевозят на грузовых машинах между городами, при этом под потоком в ребре u-v понимается количество товара, которое нужно доставить из города u в город v в течение дня. Напишите клиентскую функцию, которая выводит график работы для водителей грузовиков: где и сколько погрузить и где и сколько разгрузить. Считайте, что количество грузовиков неограничено, и распределительные пункты не начинают отгрузку, пока не получат весь товар.