Потоки в сетях

Алгоритмы поиска максимального потока расширением пути

Эффективный способ решения задачи о максимальном потоке был разработан Л.Р. Фордом (L.R. Ford) и Д.Р Фалкерсоном (D.R. Fulkerson) в 1962 г. Это обобщенный метод с постепенным увеличением потоков вдоль путей от истока к стоку, на котором основано целое семейство алгоритмов. В классической литературе он известен под названием метода Форда-Фалкерсона; широкое распространение получил также более образный термин - метод расширения пути (augmenting path method).

Рассмотрим произвольный ориентированный путь (не обязательно простой) из истока в сток st-сети. Пусть x есть минимальное значение неиспользованной пропускной способности ребер на этом пути. Мы можем увеличить поток в сети по крайней мере на x, увеличив на данную величину поток во всех ребрах этого пути. Повторяя это действие, мы выполним первую попытку вычисления потока в сети: находим другой путь, увеличиваем поток вдоль этого пути и продолжаем, пока в каждом из путей, ведущих из истока в сток, не окажется хотя бы одно заполненное ребро (и мы не сможем увеличивать потоки этим способом). В одних случаях такой алгоритм вычисляет максимальный поток, но в других случаях это ему не удается. На рис. 22.6. показан неудачный случай.

Для исправления алгоритма, чтобы он всегда находил максимальный поток, мы рассмотрим более общий способ увеличения потока вдоль произвольного пути из истока в сток в неориентированном графе, соответствующем данной сети. Ребра любого такого пути - это либо прямые (forward) ребра, направления которых совпадают с направлением потока (при следовании по пути из истока в сток мы проходим по ребру из его начальной вершины в конечную вершину), либо обратные (backward) ребра, которые направлены против потока (при следовании из истока в сток мы проходим по ребру из его конечной вершины в начальную вершину). Тогда, если существует какой-либо путь без заполненных прямых ребер и без пустых обратных ребер, можно увеличить поток в сети, увеличивая потоки в прямых ребрах и уменьшая потоки в обратных ребрах. Величина, на которую можно увеличить поток, ограничена минимумом из неиспользованных пропускных способностей и потоков в обратных ребрах. На рис. 22.12 показан соответствующий пример. В новом потоке либо заполняется одно из прямых ребер пути, либо становится пустым одно из обратных ребер этого пути.

Рис. 22.12. Расширение потока по пути

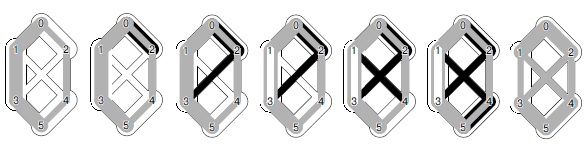
Эта последовательность демонстрирует расширение потока в сети вдоль пути из прямых и обратных ребер. Начав с потока, изображенного на левой диаграмме, и выполняя операции слева направо, мы увеличиваем поток в ребре 0-2, а затем в ребре 2-3 (дополнительные потоки показаны черным цветом). Далее мы уменьшаем поток в ребре 1-3 (показан белым цветом), отводя его в ребро 1-4, а затем в 4-5 - в результате получается поток, показанный на правой диаграмме.

Описанный процесс лежит в основе классического алгоритма Форда-Фалкерсона вычисления максимального потока (метод расширения пути). Вот его краткая формулировка:

Начинаем с нулевого потока в любом месте сети. Увеличиваем поток вдоль произвольного пути из истока в сток, содержащего незаполненные ребра или непустые обратные ребра, и продолжаем так, пока в сети не останется ни одного такого пути.

Интересно, что этот метод всегда находит максимальный поток независимо от способа выбора путей. Подобно методу вычисления MST-дерева из "Минимальные остовные деревья" и методу Беллмана-Форда поиска кратчайших путей из "Кратчайшие пути" , это обобщенный алгоритм, который полезен тем, что обосновывает правильность целого семейства более специальных алгоритмов. Для выбора путей годится любой метод.

На рис. 22.13 приведено несколько различных последовательностей расширяющих путей, каждая из которых приводит к максимальному потоку в сети. Ниже в этом разделе мы рассмотрим несколько алгоритмов, которые вычисляют последовательности расширяющих путей, и все они находят максимальный поток. Эти алгоритмы различаются по количеству расширяющих путей, которые они вычисляют, по длине путей и трудоемкости их поиска, однако все они реализуют алгоритм Форда-Фалкерсона и находят максимальный поток.

Рис. 22.13. Последовательности расширяющих путей

На этих трех примерах мы расширяем поток вдоль различных последовательностей расширяющих путей, пока не сможем найти новые расширяющие пути. В каждом случае находится максимальный поток. Важная классическая теорема из теории сетевых потоков утверждает, что мы получаем максимальный поток в любой сети, независимо от того, какую последовательность путей мы используем (см. лемму 22.5).

Чтобы показать, что любой поток, вычисленный с помощью любой реализации алгоритма Форда-Фалкерсона, и в самом деле имеет максимальную величину, мы покажем, что этот факт эквивалентен другому ключевому факту, известному как теорема о максимальном потоке и минимальном сечении (maxflow-mincut theorem). Понимание этой теоремы - очень важный шаг к пониманию алгоритмов обработки транспортных сетей. Как следует из названия, теорема основана на непосредственной взаимосвязи между потоками и сечениями в сетях, поэтому мы начнем с определения терминов, которые имеют отношение к сечениям.

Напомним, что в соответствии с определением, данным в "Минимальные остовные деревья" , сечение, или разрез (cut), графа есть разбиение множества вершин графа на два не-пересекающихся подмножества, а перекрестное ребро (crossing edge) - это ребро, соединяющее вершину одного подмножества с вершиной другого подмножества. Применительно к транспортным сетям мы уточним эти определения следующим образом (см. рис. 22.14).

Рис. 22.14. Терминология, используемая при описании st-сечений

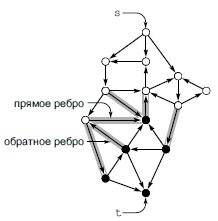
В st-сети имеется один исток s и один сток t. st-сечение - это разбиение вершин на множество, содержащее вершину s (белые кружки), и множество, содержащее вершину t (черные кружки). Ребра, связывающие вершины одного множества с вершинами другого множества (выделены серым цветом), называются секущим множеством. Прямое ребро ведет из вершины множества, содержащего s, в вершину множества, содержащего t, а обратное ребро имеет противоположное направление. В показанном здесь секущем множестве имеются четыре прямых ребра и два обратных ребра.

Каждое перекрестное ребро, соответствующее st-сечению, есть либо st-ребро, которое ведет из вершины, входящей во множество, где находится вершина s, в вершину, входящую во множество, где находится вершина t, либо ts-ребро, которое ведет в обратном направлении. Иногда множество перекрестных ребер называется секущим множеством (cut set). Пропускная способность st-сечения в транспортной сети есть сумма пропускных способностей ребер этого st-сечения, а поток через st-сечение есть разность между суммой потоков st-ребер и суммой потоков ts-ребер этого сечения. Удаление секущего множества делит связный граф на два связных компонента, удаляя все пути, соединяющие какую-либо вершину одного множества с вершиной другого множества. После удаления всех ребер, входящих в st-сечение, в сети не остается путей, соединяющих вершины s и t в соответствующем неориентированном графе, но возврат любого из них может воссоздать такой путь.

Сечения являются удобной абстракцией для приложений, перечисленных в начале текущей главы, где транспортная сеть описывает движение боеприпасов с базы в войска. Чтобы полностью прервать снабжение войск самым экономичным образом, противник должен решить следующую задачу.

Минимальное сечение. Для заданной st-сети требуется найти такое st-сечение, что пропускная способность любого другого сечения не меньше найденного. Для краткости мы будем называть такое сечение минимальным сечением (mincut), а задачу вычисления такого сечения в сети - задачей о минимальном сечении (mincut problem).

Задача о минимальном сечении представляет собой обобщение задач о связности графов, которые были кратко рассмотрены в "Поиск на графе" . Мы подробно рассмотрим конкретные взаимосвязи в разделе 22.4.

В формулировке задачи о минимальном сечении нет упоминания о потоках, и может показаться, что эти определения находятся в стороне от наших обсуждений алгоритма вычисления расширяющих путей. На первый взгляд, вычисление минимального сечения (множества ребер) выглядит более легкой задачей, чем вычисление максимального потока (назначение весов всем ребрам). Однако ключевым фактом этой главы является тесная связь задачи о максимальном потоке и задачи о минимальном сечении. Доказательством служит сам метод расширяющих путей в сочетании с двумя фактами о потоках и сечениях.

Другими словами, сечения представляют собой узкие места сети. Если в задаче армейского снабжения противник не может полностью отрезать вражеские войска от их снабжения, то он хотя бы будет уверен, что снабжение будет ограничено пропускной способностью любого заданного сечения. Естественно считать, что трудоемкость создания сечения в этом приложении пропорциональна его пропускной способности, и вражеской армии придется искать решение задачи о минимальном сечении. Но более важно то, что из этих фактов, в частности, следует, что ни один поток не может превышать пропускную способность любого минимального сечения.

Это доказательство также явно утверждает, что алгоритм Форда-Фалкерсона находит максимальный поток. Независимо от метода поиска расширяющего пути, а также независимо от того, какие пути мы найдем, он всегда находит сечение, поток которого равен его пропускной способности, и поэтому равен величине потока сети, который, следовательно, должен быть максимальным потоком.

Другое следствие правильности алгоритма Форда-Фалкерсона заключается в том, что для любой транспортной сети с целочисленными пропускными способностями ребер существует максимальный поток, в котором потоки всех ребер также принимают целочисленные значения. Каждый расширяющий путь увеличивает сетевой поток на некоторое положительное целое число (минимум из незадействованных пропускных способностей в прямых ребрах и потоков в обратных ребрах, а это всегда целые положительные значения). Отсюда и наше решение рассматривать только целочисленные пропускные способности и потоки. Можно рассматривать максимальные потоки с нецелыми величинами, даже когда все пропускные способности заданы целыми числами (см. упражнение 22.23), однако в этом нет необходимости. Это важное ограничение: обобщения, где пропускные способности и потоки измеряются вещественными числами, могут привести к неприятным аномалиям.

Рис. 22.15. Все st-сечения

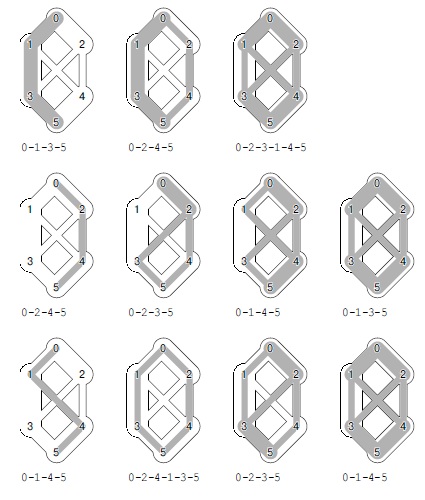
В этом списке для сети, изображенной слева, представлены все st-сечения, вершины множества, содержащего вершину s, вершины множества, содержащего вершину t, прямые ребра, обратные ребра и пропускная способность (сумма пропускных способностей прямых ребер). Для любого потока поток через все сечения (потоки в прямых ребрах минус потоки в обратных ребрах) один и тот же. Например, в случае самой левой сети поток через сечение, разделяющее вершины 0 1 3 и 2 4 5, имеет величину 2 + 1 + 2 (потоки в ребрах 0-2, 1-4 и 3-5 соответственно) минус 1 (поток в ребре 2-3), то есть 4. Эти подсчеты дают значение 4 для любого другого сечения в сети, а поток максимален, поскольку его величина равна пропускной способности минимального сечения (см. лемму 22.5). В рассматриваемой сети имеются два минимальных сечения.

Например, алгоритм Форда-Фалкерсона может привести к появлению бесконечной последовательности расширяющих путей, которая даже не сходится к величине максимального потока (см. раздел ссылок).

Обобщенный алгоритм Форда-Фалкерсона не описывает конкретный метод определения расширяющих путей. Возможно, естественнее всего использовать обобщенную стратегию поиска на графе из "Поиск на графе" . Для этого нам понадобится следующее определение.

Если ребро v-w пусто (f = 0), то в остаточной сети существует одно ребро, соответствующее v-w, с пропускной способностью с; если ребро v-w заполнено ( f = с), то в остаточной сети существует единственное ребро с пропускной способностью f, соответствующее ребру v-w; а если v-w ни заполнено, ни пусто, то в остаточную сеть входят оба ребра v-w и w-v с соответствующими пропускными способностями.