Орграфы и DAG-графы

Топологическая сортировка

Цель топологической сортировки заключается в обеспечении обработки вершин DAG-графа так, чтобы каждая вершина была обработана до всех вершин, на которые она указывает. Существуют два естественных и, по существу, эквивалентных способа определения этой базовой операции. В любом случае выполняется перестановка целых чисел от 0 до V— 1, которые, как обычно, находятся в векторах, индексированных именами вершин.

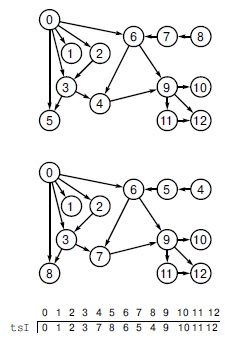
Топологическая сортировка (перенумерация). Нужно перенумеровать вершины заданного DAG-графа так, чтобы каждое ориентированное ребро вело из вершины с меньшим номером в вершину с большим номером (см. рис. 19.21).

Топологическая сортировка (переупорядочение). Нужно переупорядочить вершины заданного DAG-графа по горизонтали так, чтобы все ориентированные ребра были направлены слева направо ( рис. 19.22).

Рис. 19.21. Топологическая сортировка (перенумерация)

Для заданного произвольного DAG-графа (вверху), топологическая сортировка позволяет переименовать его вершины так, что каждое ребро будет вести из вершины с меньшим номером в вершину с большим номером (внизу). В этом примере номера вершин 4, 5, 7 и 8 заменяются, соответственно, на 7, 8 , 5 и 4, как показано в массиве tsI. Существует много возможных способов перенумерации, позволяющих получить нужный результат.

Легко установить (см. рис. 19.22), что перенумерация и переупорядочение перестановок обратны по отношению друг к другу: при наличии переупорядочения перенумерацию можно получить, присвоив номер 0 первой вершине списка, 1 второй вершине списка и т.д. Например, если в векторе ts вершины размещены в порядке топологической сортировки, то цикл

  for (i = 0; i < V; i++) tsI[ts[i]] = i;
      

определяет перенумерацию в векторе tsI, индексированном именами вершин. И можно получить переупорядочение из перенумерации с помощью цикла

  for (i = 0; i < V; i++) ts[tsI[i]] = i;
      

который помещает первой в список вершину с номером 0, потом вершину с номером 1 и т.д. Чаще всего мы будем называть топологической сортировкой (topological sort) вариант задачи с переупорядочением. Обратите внимание, что ts не есть вектор, индексированный именами вершин. Обычно порядок вершин, устанавливаемый топологической сортировкой, не уникален. Например,

8 7 0 1 2 3 6 4 9 10 11 12 5

0 1 2 3 8 6 4 9 10 11 12 5 7

0 2 3 8 6 4 7 5 9 10 1 11 12

8 0 7 6 2 3 4 9 5 1 11 12 10

— верные топологические сортировки для примера, представленного на рис. 19.6 (существует и множество других). При составлении расписаний подобная ситуация возникает всякий раз, когда одна из задач не находится в прямой или косвенной зависимости от другой задачи, и поэтому может выполняться либо до, либо после этой задачи (или даже одновременно). При увеличении количества таких пар задач количество возможных расписаний возрастает экспоненциально.

Как уже было сказано, иногда полезно рассматривать ребра орграфа по-другому: если ребро направлено из s в t, это означает, что вершина s " зависит " от вершины t. Например, вершины могут представлять определения терминов в некоторой книге — тогда ребро направлено из s в t, если в определении s используется определение t. В этом случае нужно найти упорядочение, при котором определение каждого термина дается перед тем, как оно будет использовано в другом определении. Подобное упорядочение соответствует такому выстраиванию вершин в ряд, что все ребра будут направлены справа налево — это обратная топологическая сортировка (reverse topological sort). На рис. 19.23 показана обратная топологическая сортировка на нашем примере DAG.

Но, оказывается, мы уже знакомы с алгоритмом обратной топологической сортировки: это наш старый знакомый — стандартный рекурсивный поиск в глубину! Если входным графом является DAG, то обратная нумерация размещает вершины в обратном топологическом порядке. То есть последним действием рекурсивная функция DFS нумерует каждую вершину так же, как в векторе post в программе 19.2. Как видно из рис. 19.24, эта нумерация эквивалентна обратной нумерации узлов в лесе DFS и обеспечивает топологическую сортировку: вектор post, индексированный именами вершин, выполняет перенумерацию, а обратный ему вектор (см. рис. 19.23) — обратную топологическую сортировку DAG-графа.

Рис. 19.22. Топологическая сортировка (переупорядочение)

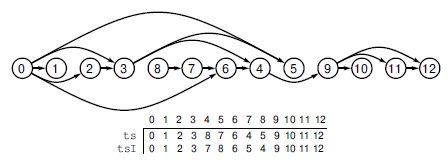
Эта диаграмма позволяет по-другому взглянуть на топологическую сортировку, представленную на рис. 19.21: в ней определяется способ переупорядочения, а не перенумерации вершин. Если разместить вершины в порядке, указанном в массиве ts, слева направо, то все ориентированные ребра будут направлены вправо. Инверсия перестановки ts есть перестановка tsI, которая определяет перенумерацию, приведенную на рис. 19.21.

Рис. 19.23. Обратная топологическая сортировка

В этой обратной топологической сортировке нашего демонстрационного орграфа все ребра направлены справа налево. Нумерация вершин, заданная обратной перестановкой tsI, порождает граф, в котором каждое ребро направлено из вершины с большим номером в вершину с меньшим номером.

Рис. 19.24. Лес DFS для DAG-графа

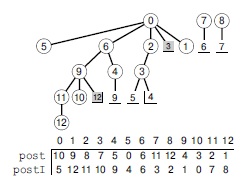
Лес DFS заданного орграфа не имеет обратных ребер (ребер, ведущих в узлы с большими обратными номерами) тогда и только тогда, когда этот орграф является DAG-графом. Ребра, не принадлежащие деревьям в этом лесе DFS для DAG-графа с рис. 19.21 — это либо нисходящие ребра (серые квадратики), либо поперечные ребра (белые квадратики). Последовательность посещения вершин при обратном обходе леса, показанная внизу, представляет собой обратную топологическую сортировку (см. рис. 19.23).

Итак, стандартный поиск в глубину можно легко адаптировать для выполнения топологической сортировки, как показано в программе 19.6. Эта реализация выполняет обратную топологическую сортировку: она вычисляет перестановку обратной нумерации и ее инверсию, чтобы клиенты могли как перенумеровывать, так и переупорядочивать вершины.

Программа 19.6. Обратная топологическая сортировка

Этот класс DFS вычисляет обратную нумерацию леса DFS (обратная топологическая сортировка). Клиенты могут использовать объект TS для перенумерации вершин DAG-графа, чтобы каждое ребро вело из вершины с большим номером в вершину с меньшим номером, либо переупорядочить вершины так, чтобы начальная вершина каждого ребра появлялась после конечной вершины (см. рис. 19.23).

  template <class Dag>
  class dagTS
    { const Dag &D;
      int cnt, tcnt;
      vector<int> pre, post, postI;
      void tsR(int v)
        { pre[v] = cnt++;
          typename Dag::adjIterator A(D, v);
          for (int t = A.beg(); !A.end(); t = A.nxt())
            if (pre[t] == -1) tsR(t);
          post[v] = tcnt; postI[tcnt++] = v;
        }
    public:
      dagTS(const Dag &D) : D(D), tcnt(0), cnt(0),
        pre(D.V(), -1), post(D.V(), -1), postI(D.V(), -1)
        { for (int v = 0; v < D.V(); v++)
          if (pre[v] == -1) tsR(v);
        }
      int operator[](int v) const { return postI[v]; }
      int relabel(int v) const { return post[v]; }
    };
      

С вычислительной точки зрения различие между обычной и обратной топологической сортировкой невелико. Достаточно просто изменить операцию [] так, чтобы она возвращала значение postI[G.V()-1-v], либо изменить реализацию одним из следующих способов:

• Выполните обратную топологическую сортировку на обращении заданного DAG-графа.
• Последним действием рекурсивной процедуры не используйте номер вершины в качестве индекса для обратной нумерации, а поместите ее в стек. После завершения просмотра останется вытолкнуть вершины из стека — они будут выходить в топологическом порядке.
• Пронумеруйте вершины в обратном порядке (от V— 1 до 0). При желании вычислите обращение нумерации вершин, чтобы получить топологический порядок.

Доказательство того, что эти изменения позволяют получить правильное топологическое упорядочение, оставляем на самостоятельную проработку (см. упражнение 19.97).

Для реализации первого из перечисленных вариантов для разреженных графов (представленных списками смежности) может потребоваться программа 19.1 для вычисления обратного графа. Это удваивает объем необходимой памяти, что нежелательно в случае крупных графов. Что касается насыщенных графов (представленных матрицей смежности), то, как было сказано в разделе 19.1, можно выполнить поиск в глубину на обратном графе без дополнительной памяти и лишней работы — просто заменив строки на столбцы при обращении к матрице смежности (см. программу 19.7).

Программа 19.7. Топологическая сортировка

Если использовать данную реализацию функции tsR в программе 19.6, то конструктор вычислит топологическую сортировку, но не ее обращение (для любой реализации DAG, которая поддерживает функцию edge), поскольку она заменяет вызов edge(v, w) при поиске в глубину на edge(w, v), т.е. обрабатывает обратный граф (см. текст).

  void tsR(int v)
    { pre[v] = cnt++;
      for (int w = 0; w < D.V(); w++)
        if (D.edge(w, v))
          if (pre[w] == -1) tsR(w);
      post[v] = tcnt; postI[tcnt++] = v;
    }
      

А теперь мы рассмотрим альтернативный классический метод топологической сортировки, который больше похож на поиск в ширину (BFS, см. "Поиск на графе" ). Он основан на следующем свойстве DAG-графов.

Из этого факта можно вывести алгоритм топологической сортировки: пометим любой исток наименьшей неиспользованной меткой, затем удалим его и пометим остальную часть DAG-графа, используя тот же алгоритм. На рис. 19.25 рис. 19.25 показана трасса работы этого алгоритма на нашем демонстрационном DAG-графе.

Эффективная реализация этого алгоритма — классическое упражнение по проектированию структур данных (см. раздел ссылок). Во-первых, истоков может быть несколько, и понадобится очередь для их хранения (подойдет любая обобщенная очередь). Во-вторых, необходимо находить истоки в DAG-графе после удаления какого-либо истока. Эту задачу можно выполнить с помощью вектора, индексированного именами вершин, в котором учитываются степени захода каждой вершины. Вершины со степенью захода 0 являются истоками, поэтому можно инициализировать очередь одним просмотром DAG-графа (используя поиск в глубину или любой другой метод, который просматривает все ребра). Затем, пока очередь истоков не опустеет, мы выполняем следующие операции:

• Удаляем исток из очереди и присваиваем ему номер.
• Уменьшаем на единицу значения в векторе степеней захода, соответствующие конечным вершинам ребер, выходящих из удаленной вершины.
• Если при уменьшении значения какой-либо элемент становится равным 0, заносим соответствующую вершину в очередь истоков.

Программа 19.8 содержит реализацию этого метода, в которой применяется очередь FIFO, а на рис. 19.26 показан пример ее работы на нашем демонстрационном DAG-графе, который раскрывает дополнительные подробности динамики примера на рис. 19.25.

Рис. 19.25. Топологическая сортировка DAG-графа методом удаления истоков

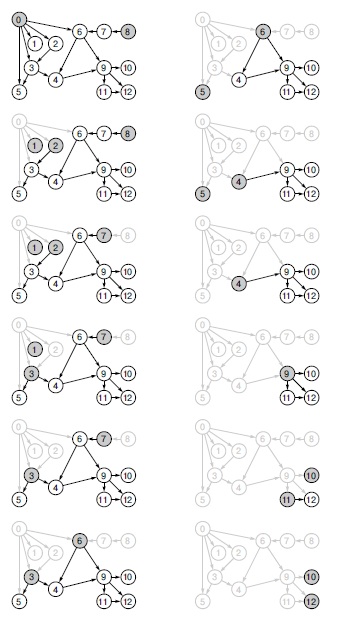
Вершина 0 является истоком (на нее не указывает ни одно ребро) и поэтому может оказаться первой при топологической сортировке этого графа (слева вверху). Если удалить вершину 0 (и все ребра из нее в другие вершины), то истоками в полученном DAG-графе станут вершины 1 и 2 (слева, вторая диаграмма сверху), и этот граф можно сортировать при помощи того же алгоритма. На данном рисунке показано действие программы 19.8, которая выбирает один из истоков (серые узлы на каждой диаграмме), используя дисциплину FIFO, хотя на каждом шаге может быть выбран любой из источников. На рис. 19.26 представлено содержимое структур данных, управляющих выбором действий алгоритма. Результатом топологической сортировки, показанной на этом рисунке, является следующий порядок узлов: 0 8 2 1 7 3 6 5 4 9 11 10 12.

Программа 19.8. Топологическая сортировка с очередью истоков

Этот класс реализует тот же интерфейс, что и программы 19.6 и 19.7. В нем используется очередь истоков и таблица для хранения степеней захода всех вершин DAG-графа, индуцированного вершинами, которые еще не удалены из очереди.

При удалении истока из очереди мы уменьшаем значения степеней захода, соответствующих каждой вершине в его списке смежности (и заносим в очередь все вершины, соответствующие нулевым элементам таблицы). Вершины извлекаются из очереди в порядке топологической сортировки.

    #include "QUEUE.cc"
    template <class Dag>
    class dagTS
      { const Dag &D;
        vector<int> in, ts, tsI;
      public:
        dagTS(const Dag &D) : D(D), in(D.V(), 0), ts(D.V(), -1), tsI(D.V(), -1)
        { QUEUE<int> Q;
          for (int v = 0; v < D.V(); v++)
            { typename Dag::adjIterator A(D, v);
              for (int t = A.beg(); !A.end(); t = A.nxt())
                in[t]+ + ;
            }
          for (int v = 0; v < D.V(); v++)
            if (in[v] == 0) Q.put(v);
          for (int j = 0; !Q.empty(); j++)
            { ts[j] = Q.get(); tsI[ts[j]] = j;
              typename Dag::adjIterator A(D, ts[j]);
              for (int t = A.beg(); !A.end(); t = A.nxt())
                if (—in[t] == 0) Q.put(t);
            }
        }
        int operator[](int v) const { return ts[v]; }
        int relabel(int v) const { return tsI[v]; }
      };
      

Рис. 19.26. Таблица степеней захода и содержимое очереди

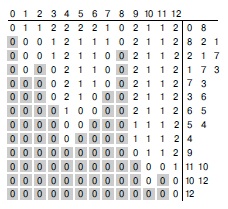
Здесь показаны содержимое таблицы степеней захода (слева) и очередь истоков (справа) во время выполнения программы 19.8 на DAG-графе, соответствующем рис. 19.25. В любой заданный момент времени очередь истоков содержит узлы с нулевыми степенями захода. Просматривая сверху вниз, мы извлекаем из очереди истоков самый левый узел, уменьшаем на единицу степени захода элементов, соответствующих каждому ребру, исходящему из этого узла, и заносим в очередь истоков все вершины, элементы которых стали равными 0. Например, вторая строка таблицы отражает результат удаления вершины 0 из очереди истоков, с последующим (поскольку DAG содержит ребра 0-1, 0-2, 0-3, 0-5 и 0-6) уменьшением на единицу элементов, соответствующих вершинам 1, 2, 3, 5 и 6, и занесением вершин 2 и 1 в очередь истоков (поскольку значения их степеней захода стали равными 0). Считывание самых левых элементов в очереди истоков сверху вниз дает топологическое упорядочение рассматриваемого графа.

Очередь истоков не опустеет, пока не будут помечены все вершины DAG-графа, т.к. подграф, индуцированный еще не помеченными вершинами, всегда является DAG-графом, а у каждого DAG-графа имеется хотя бы один исток. Вообще-то этот алгоритм можно использовать для проверки, является ли заданный граф DAG-графом: ведь если очередь опустеет до того, как все вершины будут помечены, то в подграфе, индуцированном еще непомеченными вершинами, должен существовать цикл (см. упражнение 19.104).

Обработка вершин в порядке, заданном топологической сортировкой, лежит в основе обработки DAG-графов. Классическим примером может служить задача вычисления длины самого длинного пути в DAG-графе. Рассматривая вершины в обратном топологическом порядке, легко вычислить самый длинный путь, начинающийся в каждой вершине v. Для этого нужно добавить единицу к максимальной из длин самых длинных путей, которые начинаются в каждой из вершин, достижимых из v через одно ребро. Благодаря топологической сортировке все такие длины известны во время обработки вершины v, поэтому никакие другие пути из v после этого выявлены не будут.

Например, просматривая слева направо обратную топологическую сортировку, показанную на рис. 19.23, можно быстро вычислить следующую таблицу длин максимальных путей, начинающихся в каждой вершине демонстрационного графа с рис. 19.21: 5 12 11 10 9 4 6 3 2 1 0 7 8 0 0 1 0 2 3 4 4 5 0 6 5 6

Например, значение 6, соответствующее 0 (третий столбец справа), означает, что существует путь длиной 6, начинающийся в 0. Ведь существует ребро 0-2, а ранее мы определили, что длина самого длинного пути из вершины 2 равна 5, и что ни одно из ребер, исходящих из 0, не ведет в узел, имеющий более длинный путь.

При использовании топологической сортировки для подобных приложений необходимо реализовать один из следующих способов разработки:

• Использование класса DAGts в АТД DAG с последующей обработкой вершин в очередности, задаваемой вычисленным вектором.
• Обработка вершин после рекурсивных вызовов при выполнении поиска в глубину.
• Обработка вершин при извлечении их из очереди в процессе топологической сортировки на основе очереди истоков.

Все эти методы используются в реализациях, выполняющих обработку DAG — важно только знать, что все они эквивалентны. Другие приложения топологической сортировки будут рассмотрены в упражнениях 19.111 и 19.114 и в разделах 19.7 и 21.4.

Упражнения

19.92. Напишите функцию, которая проверяет, является ли заданная перестановка вершин DAG-графа верной топологической сортировкой этого графа.

19.93. Сколько возможно различных топологических сортировок для DAG-графа, изображенного на рис. 19.6?

19.94. Приведите лес DFS и обратную топологическую сортировку, которые получаются в результате выполнения стандартного поиска в глубину по спискам смежности (с обратной нумерацией) следующего DAG-графа:

3-71-47-80-55-23-82-90-64-92-66-44-32-3.

19.95. Приведите лес DFS и обратную топологическую сортировку, которые получаются при построении стандартного представления списками смежности для DAG-графа

3-71-47-80-55-23-82-90-64-92-66-44-32-3

с последующим обращением с помощью программы 19.1 и выполнением поиска в глубину по спискам смежности с обратной нумерацией.

19.96. В программе 19.6 для выполнения обратной топологической сортировки используется обратная нумерация. Почему нельзя воспользоваться прямой нумерацией? Обоснуйте свой ответ на примере графа с тремя вершинами.

19.97. Докажите правильность каждого из трех предложенных в тексте модификаций поиска в глубину с обратной нумерацией — то есть что вычисляется именно прямая, а не обратная топологическая сортировка.

19.98. Приведите лес DFS и топологическую сортировку, которые получаются в результате выполнения стандартного поиска в глубину с неявным обращением на представлении списками смежности (и обратной нумерацией) для следующего DAG-графа:

3-71-47-80-55-23-82-90-64-92-66-44-32-3(см.про грамму19.7).

19.99. Пусть задан некоторый DAG-граф. Существует ли топологическая сортировка, которую нельзя получить алгоритмом на основе поиска в глубину, независимо от порядка выбора вершин, смежных с текущей? Обоснуйте свой ответ.

19.100. Покажите в стиле рис. 19.26 процесс топологической сортировки DAG-графа

3-71-47-80-55-23-82-90-64-92-66-44-32-3 с помощью алгоритма, использующего очередь истоков (программа 19.8).

19.101. Приведите топологическую сортировку, которая получится, если в примере, представленном на рис. 19.25, в качестве структуры данных использовать стек, а не очередь.

19.102. Пусть задан некоторый DAG-граф. Существует ли топологическая сортировка, которую нельзя получить алгоритмом на основе поиска в глубину, независимо от дисциплины, реализуемой очередью? Обоснуйте свой ответ.

19.103. Измените алгоритм топологической сортировки с очередью истоков, чтобы в нем использовалась обобщенная очередь. Воспользуйтесь модифицированным алгоритмом с очередью LIFO, стеком и рандомизированной очередью.

19.104. Воспользуйтесь программой 19.8 для реализации класса, проверяющего отсутствие циклов в заданном DAG-графе (см. упражнение 19.75).

19.105. Преобразуйте алгоритм топологической сортировки с очередью истоков в алгоритм с очередью стоков для выполнения обратной топологической сортировки.

19.106. Напишите программу, которая генерирует все возможные топологические упорядочения заданного DAG-графа, либо, если количество таких упорядочений превышает границу, заданную в качестве аргумента, просто выводит это число.

19.107. Напишите программу, которая преобразует любой орграф с V вершинами и E ребрами в DAG-граф, выполнив топологическую сортировку на основе DFS и изменяя направление каждого встреченного обратного ребра. Докажите, что эта стратегия всегда приводит к созданию DAG-графа.

19.108. Напишите программу, которая генерирует с равной вероятностью один из возможных DAG-графов с V вершинами и E ребрами (см. упражнение 17.70).

19.109. Сформулируйте необходимые и достаточные условия существования для конкретного DAG-графа только одного возможного топологического упорядочения его вершин.

19.110. Эмпирически сравните алгоритмы топологической сортировки, приведенные в этом разделе, для различных DAG-графов (см. упражнения 19.2, 19.76, 19.107 и 19.108). Протестируйте свою программу, как описано в упражнении 19.11 (для разреженных графов) и в упражнении 19.12 (для насыщенных графов).

19.111. Измените программу 19.8 так, чтобы она могла вычислять количество различных простых путей из любого истока в каждую вершину DAG-графа.

19.112. Напишите класс, который вычисляет DAG-графы, представляющие арифметические выражения (см. рис. 19.19 рис. 19.19). Для хранения значений, соответствующих каждой вершине, используйте вектор, индексированный именами вершин. Предполагается, что значения, соответствующие листьям, заданы заранее.

19.113. Опишите семейство арифметических выражений, таких, что размер дерева выражения экспоненциально больше, чем размер соответствующего DAG-графа (и поэтому время выполнения программы из упражнения 19.112 для этого DAG пропорционально логарифму времени выполнения для дерева).

19.114. Разработайте метод поиска простого ориентированного пути максимальной длины в DAG-графе за время, пропорциональное V. Используйте этот метод для реализации класса, выполняющего вывод гамильтонова пути в заданном DAG-графе, если он существует.