Орграфы и DAG-графы

Достижимость в DAG-графах

В завершение нашего изучения DAG-графов мы рассмотрим задачу вычисления транзитивного замыкания DAG-графа. Можно ли разработать алгоритмы для DAG-графов, более эффективные, чем алгоритмы для обобщенных орграфов, которые были рассмотрены в разделе 19.3?

Любой метод топологической сортировки может служить основой алгоритмов транзитивного замыкания DAG: мы просматриваем вершины в обратном топологическом порядке, вычисляя при этом вектор достижимости для каждой вершины (то есть строку матрицы транзитивного замыкания) из строк, соответствующих смежным с ней вершинам. Обратная топологическая сортировка гарантирует, что все эти строки уже вычислены тогда, когда они нужны. Мы проверяем каждый из V элементов вектора, соответствующих конечным вершинам каждого из E ребер, на что в общем нужно время, пропорциональное VE. Этот метод легко реализовать, но он обрабатывает DAG-графы ничуть не эффективнее, чем орграфы общего вида.

При использовании стандартного поиска в глубину для топологической сортировки (см. программу 19.7) можно повысить ее производительность для некоторых видов DAG-графов, как показано в программе 19.9. Поскольку в DAG-графах не может быть циклов, то при поиске в глубину не может быть обратных ребер. Однако важнее то, что как поперечные, так и нисходящие ребра ведут в узлы, в которых DFS уже завершен. Чтобы воспользоваться этим, мы разработаем рекурсивную функцию, которая вычисляет все вершины, достижимые из заданной исходной вершины, но (как обычно при поиске в глубину) без рекурсивных вызовов для вершин, для которых уже вычислено множество достижимых вершин. В этом случае достижимые вершины представлены одной из строк транзитивного замыкания, а рекурсивная функция выполняет операцию логического ИЛИ над всеми строками, соответствующими смежным вершинам. В случае древесных ребер выполняется рекурсивный вызов для вычисления этой строки; в случае поперечных ребер можно пропустить рекурсивный вызов, т.к. мы знаем, что эта строка уже была вычислена в результате предыдущего рекурсивного вызова; в случае нисходящих ребер можно пропустить все вычисление, поскольку любые достижимые узлы, которые могут быть при этом добавлены, уже учтены в множестве достижимых узлов для конечной вершины (ниже и раньше в дереве DFS).

Рис. 19.27. Транзитивное замыкание DAG-графа

Данная последовательность векторов-строк представляет транзитивное замыкание DAG-графа с рис. 19.21. Эти строки вычислены в обратном топологическом порядке последним действием рекурсивной функции DFS (см. программу 19.9). Каждая строка является результатом логической операции ИЛИ над строками для смежных вершин, которые находятся раньше в списке. Например, чтобы вычислить строку для вершины 0, мы выполняем логическую ИЛИ над строками для вершин 5, 2, 1 и 6 (и заносим значение 1, соответствующее самой вершине 0), т.к.ребра 0-5, 0-2, 0-1 и 0-6 приводят нас из вершины 0 в вершины, достижимые из каждой из этих вершин. Нисходящие ребра можно игнорировать, поскольку они не добавляют новой информации. Например, мы игнорируем ребро, ведущее из 0 в 3, потому что вершины, достижимые из 3, уже учтены в строке, соответствующей вершине 2.

Использование этого варианта поиска в глубину можно считать применением динамического программирования для вычисления транзитивного замыкания, т.к. мы используем уже вычисленные (и сохраненные в строках матрицы смежности, которые соответствуют ранее обработанным вершинам) результаты, чтобы не выполнять ненужных рекурсивных вызовов. На рис. 19.27 показано вычисление транзитивного замыкания DAG-графа с рис. 19.6.

Программа 19.9. Транзитивное замыкание DAG-графа

Конструктор этого класса вычисляет транзитивное замыкание DAG при помощи одного поиска в глубину. Он рекурсивно вычисляет вершины, достижимые из всех потомков каждой вершины в дереве DFS.

  template <class tcDag, class Dag>
  class dagTC
    { tcDag T; const Dag &D;
      int cnt;
      vector<int> pre;
      void tcR(int w)
        { pre[w] = cnt++;
          typename Dag::adjIterator A(D, w);
          for (int t = A.beg(); !A.end(); t = A.nxt())
            { T.insert(Edge(w, t));
              if (pre[t] > pre[w]) continue;
              if (pre[t] == -1) tcR(t);
              for (int i = 0; i < T.V(); i++)
                if (T.edge(t, i)) T.insert(Edge(w, i));
            }
        }
    public:
      dagTC(const Dag &D) : D(D), cnt(0),
        pre(D.V(), -1), T(D.V(), true)
        { for (int v = 0; v < D.V(); v++)
          if (pre[v] == -1) tcR(v);
        }
      bool reachable(int v, int w) const
        { return T.edge(v, w); }
    } ;
      

Если в DAG-графе нет нисходящих ребер (см. упражнение 19.42), время выполнения программы 19.9 пропорционально VE — т.е. она ничем не лучше алгоритмов транзитивного замыкания для орграфов общего вида из раздела 19.3 (см., например, программу 19.4) или подхода на основе топологической сортировки, которая описана в начале данного раздела. Однако при большом количестве нисходящих ребер (или, что одно и то же, при малом количестве поперечных ребер) программа 19.9 работает значительно быстрее этих методов.

Задача поиска оптимального алгоритма (гарантирующего выполнение за время, пропорциональное V² ) вычисления транзитивного замыкания для насыщенных DAG-графов все еще не решена. Лучшая известная граница производительности для худшего случая равна VE. Но, конечно, лучше использовать алгоритм, который работает быстрее для большого класса DAG-графов — например, программу 19.9 — чем алгоритм, который, как программа 19.4, всегда выполняется за время, пропорциональное VE. В разделе 19.9 мы убедимся, что такое повышение производительности для DAG-графов оказывает непосредственное влияние и на нашу способность вычислять транзитивные замыкания орграфов общего вида.

Упражнения

19.115. Покажите в стиле рис. 19.27 векторы достижимости, если для вычисления транзитивного замыкания DAG-графа

3-71-47-80-55-23-82-90-64-92-66-44-32-3

использовать программу 19.9.

19.116. Разработайте такую версию программы 19.9, которая использует представление транзитивного замыкания без поддержки функции проверки edge и которая выполняется за время, пропорциональное 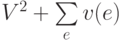, где суммирование проводится по всем ребрам DAG-графа, а v(e) — количество вершин, достижимых из конечной вершины ребра е. Для некоторых видов разреженных DAG-графов такие затраты существенно меньше, чем VE (см. упражнение 19.65).

19.117. Реализуйте класс абстрактного транзитивного замыкания для DAG-графов, который использует дополнительный объем памяти, не более чем пропорциональный V (и пригодный для работы с крупными DAG-графами). Воспользуйтесь топологической сортировкой для получения быстрого ответа, если вершины не связаны, а также реализацией очереди истоков, чтобы возвращать длину пути, когда вершины связаны.

19.118. Разработайте реализацию транзитивного замыкания на основе обратной топологической сортировки с очередью стоков (см. упражнение 19.105).

19.119. Требует ли ваше решение задачи 19.118 просмотра всех ребер DAG-графа или игнорирует некоторые ребра — например, нисходящие ребра в DFS? Приведите пример, когда необходим просмотр всех ребер, или опишите ребра, которые можно пропустить.