Поиск на графе

Обобщенный поиск на графах

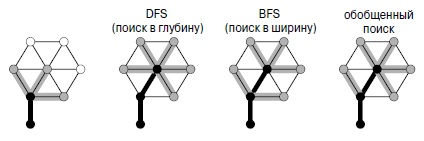
Алгоритмы DFS и BFS — фундаментальные и важные методы, лежащие в основе многочисленных алгоритмов обработки графов. Зная их основные свойства, мы можем перейти на более высокий уровень абстракции, на котором видно, что оба метода представляют собой частные случаи обобщенной стратегии перемещения по графу — той, которая была предложена в реализацию поиска в ширину (программа 18.9).

Основной принцип прост: мы снова обращаемся к описанию поиска в ширину из раздела 18.6, только вместо понятия очередь (queue) используем обобщенный термин накопитель (fringe) — множество ребер-кандидатов для следующего включения в дерево поиска. Мы сразу же приходим к общей стратегии поиска связного компонента графа. Начав с петли исходной вершины в накопителе и пустого дерева, выполняем следующую операцию, пока накопитель не станет пустым:

Перенесите какое-либо ребро из накопителя в дерево. Если вершина, в которую оно ведет, еще не посещалась, посетите эту вершину и поместите в накопитель все ребра, которые ведут из этой вершины в еще не посещенные вершины.

Эта стратегия описывает семейство алгоритмов поиска, которые обеспечивают посещение всех вершин и ребер связного графа независимо от того, какой тип обобщенной очереди используется для хранения ребер в накопителе.

Если для реализации накопителя использовать очередь, получится поиск в ширину, описанный в разделе 18.6. Если для реализации накопителя использовать стек, получится поиск в глубину. Это явление подробно представлено на рис. 18.25, который полезно сравнить с рисунками 18.6 и 18.21.

Доказательство эквивалентности рекурсивного DFS и DFS на базе стека представляет собой интересное упражнение по удалению рекурсии, в процессе которого стек, лежащий в основе рекурсивной программы, фактически преобразовывается в стек, реализующий накопитель (см. упражнение 18.63). Порядок просмотра в DFS, показанный на рис. 18.25, отличается от порядка просмотра на рис. 18.6 только тем, что из-за дисциплины LIFO ребра, инцидентные каждой вершине, проверяются в порядке, обратном порядку в матрице смежности (или в списках смежности). Однако главное не меняется: если изменить структуру данных в программе 18.8 с очереди на стек (что легко сделать, поскольку интерфейсы АТД этих двух структур данных отличаются только именами функций), то программа будет выполнять поиск не в ширину, а в глубину.

Как было сказано в разделе 18.7, этот обобщенный метод может оказаться не таким эффективным, как хотелось бы, поскольку накопитель оказывается загроможден ребрами, указывающими на вершины, которые уже были перенесены в дерево, когда данное ребро находилось в накопителе. В случае очередей FIFO этого удается избежать благодаря пометке конечных вершин в момент занесения их в очередь. Мы игнорируем ребра, которые ведут в вершины, находящиеся в накопителе, поскольку знаем, что они не будут использованы: старое ребро (и посещенная вершина) извлекается из очереди раньше, чем новое (см. программу 18.9). В реализации со стеком все наоборот: когда в накопитель нужно поместить ребро с той же конечной вершиной, что и уже хранящееся ребро, мы знаем, что не будет использовано старое ребро, поскольку новое ребро (и посещенная вершина) извлекается из стека раньше старого. Чтобы охватить эти два крайних случая и обеспечить возможность реализации накопителя, которая может воспользоваться какой-нибудь другой стратегией, блокирующей наличие в накопителе ребер, которые указывают на ту же вершину, мы скорректируем нашу обобщенную схему следующим образом:

Выберите из накопителя ребро и перенесите его в дерево. Посетите вершину, в которую оно ведет, и поместите в накопитель все ребра, которые ведут из этой вершины в еще не посещенные вершины, руководствуясь стратегией замены в накопителе, которая гарантирует, что никакие два ребра в накопителе не указывают на одну и ту же вершину (р рис. 18.26).

Рис. 18.25. Алгоритм поиска в глубину с использованием стека

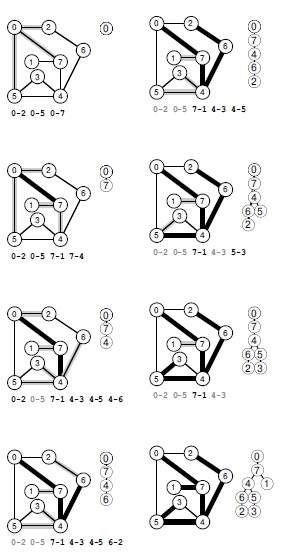
Вместе с рис. 18.21 данный рисунок демонстрирует, что поиски в ширину и в глубину отличаются друг от друга только рабочей структурой данных. Для поиска в ширину используется очередь, а для поиска в глубину — стек. Выполнение начинается с просмотра всех вершин, смежных с исходной вершиной (вверху слева). Затем мы перемещаем ребро 0-7 из стека в дерево и заталкиваем в стек инцидентные вершине 7 ребра 7-1, 7-4 и 7-6, которые ведут в еще не включенные в дерево вершины (вторая диаграмма сверху слева). Дисциплина LIFO предполагает, что при помещении ребра в стек другие ребра, ведущие в ту же вершину, считаются неактуальными и игнорируются, когда поднимаются в верхушку стека. Эти ребра заштрихованы на рисунке серым цветом. После этого мы переносим ребро 7-6 из стека в дерево и заносим инцидентные ему ребра в стек (третья диаграмма сверху слева). Потом мы извлекаем из стека ребро 4-6 и заносим инцидентные ему ребра, два из которых приводят нас к новым вершинам (внизу слева). В завершение поиска мы извлекаем из стека оставшиеся ребра, игнорируя " серые " ребра, когда они поднимаются в верхушку стека (справа).

Стратегия блокировки одинаковых конечных вершин в накопителе позволяет отказаться от проверки, была ли посещена конечная вершина извлеченного из очереди ребра. В случае поиска в ширину используется реализация очереди с правилом игнорирования новых элементов, а для поиска в глубину нужен стек с правилом игнорирования старых элементов. Однако любая обобщенная очередь в сочетании с любым правилом блокировки также даст эффективный метод просмотра всех вершин и ребер графа за линейное время с использованием объема дополнительной памяти, пропорционального V. Схематическая иллюстрация этих различий приведена на рис. 18.27. Так что в нашем распоряжении имеется целое семейство стратегий поиска на графе, которое содержит и BFS, и DFS, и члены которого отличаются друг от друга только реализацией обобщенной очереди. Как мы увидим ниже, в это семейство входят и многие другие классические алгоритмы обработки графов.

В программе 18.10 представлена реализация этих идей для графов, представленных списками смежности. Она помещает ребра накопителя в обобщенную очередь и использует обычные векторы, индексированные именами вершин, для идентификации вершин в накопителе, чтобы можно было воспользоваться явной операцией АТД обновить, когда встречается другое ребро, ведущее в вершину, которая уже занесена в накопитель. Конкретная реализация АТД может выбирать, игнорировать ли ей новое ребро или заменить им старое ребро.

Рис. 18.26. Терминология поиска на графе

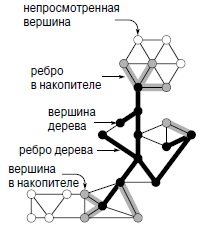
Для выполнения поиска на графе мы используем дерево поиска (черные линии) и накопитель (серые линии), содержащие ребра, которые являются кандидатами на следующее включение в дерево. Любая вершина либо занесена в дерево (черные), либо находится в накопителе (серые), либо еще не просмотрена (белые). Вершины дерева соединены древесными ребрами, а каждая вершина из накопителя соединена ребром с некоторой вершиной дерева.

Рис. 18.27. Стратегии поиска на графе

Здесь показаны различные возможности при выборе следующего шага поиска, показанного на рис. 18.26. Мы переносим вершину из накопителя в дерево (из центра колеса, вверху справа), проверяем все ее ребра и помещаем ребра, ведущие в непроверенные вершины, в накопитель. При этом используется правило замещения, которое определяет обработку ребер, указывающих на вершины, которые уже присутствуют в накопителе и указывают на ту же самую вершину: нужно ли пропустить такое ребро или заменить им ребро из накопителя. В поиске в глубину мы всегда заменяем старые ребра, а в поиске в ширину — всегда игнорируем новые ребра; в других стратегиях мы заменяем одни ребра и пропускаем другие.

Программа 18.10. Обобщенный поиск на графе

Данный класс поиска на графе обобщает алгоритмы BFS и DFS и поддерживает другие алгоритмы обработки графов (см. "Кратчайшие пути" , в котором обсуждаются эти алгоритмы и альтернативные реализации). В нем используется обобщенная очередь ребер, которая называется накопителем (fringe). Вначале в накопитель заносится петля исходной вершины; затем, пока накопитель не пуст, мы переносим из него ребро e в дерево (с началом в вершине e.v) и просматриваем список смежности вершины e.w, помещая в накопитель непросмотренные вершины и вызывая функцию update при появлении новых ребер, указывающих на вершины, которые уже занесены в накопитель.

Этот код использует векторы ord и st, чтобы никакие два ребра в накопителе не указывали на одну и те же вершину. Вершина v является конечной вершиной ребра, помещенного в накопитель, тогда и только тогда, когда она помечена (значение ord[v] не равно -1), но еще не находится в дереве (st[v] равно -1).

  #include "GQ.cc"
  template <class Graph>
  class PFS : public SEARCH<Graph>
    { vector<int> st;
      void searchC(Edge e)
        { GQ<Edge> Q(G.V());
          Q.put(e); ord[e.w] = cnt++;
          while (!Q.empty())
            { e = Q.get(); st[e.w] = e.v;
              typename Graph::adjIterator A(G, e.w);
              for (int t = A.beg(); !A.end(); t = A.nxt())
                if (ord[t] == -1)
                  { Q.put(Edge(e.w, t)); ord[t] = cnt++; }
              else
                if (st[t] == -1) Q.update(Edge(e.w, t));
            }
        }
    public:
      PFS(Graph &G) : SEARCH<Graph>(G), st(G.V(), -1)
        { search(); }
      int ST(int v) const { return st[v]; }
    } ;
      

Существует множество других заслуживающих внимания эффективных моделей АТД накопителя. Например, как в случае нашей первой реализации BFS, можно придерживаться нашей первой общей схемы: просто поместить все ребра в накопитель, а при извлечении из накопителя игнорировать те их них, которые ведут в вершины, уже включенные в дерево. Недостаток такого подхода, как и в случае BFS, состоит в том, что максимальный размер очереди должен быть равен E, а не V. Либо можно выполнять обновления неявно в реализации АТД, просто указав, что никакие два ребра с одной и той же конечной вершиной не могут находиться в очереди одновременно. Однако простейший способ сделать это в реализации АТД по сути эквивалентен использованию вектора, индексированного именами вершин (см. упражнения 4.51 и 4.54), поэтому такая проверка больше вписывается в клиентские программы, выполняющие поиск на графе.

Сочетание программы 18.10 с абстракцией обобщенной очереди дает универсальный и гибкий механизм поиска на графе. Для иллюстрации этого утверждения мы кратко рассмотрим две интересных и полезных альтернативы поискам в глубину и ширину.

Первая альтернативная стратегия основана на использовании рандомизированной очереди (randomized queue, см. "Абстрактные типы данных" ). Из рандомизированных очередей элементы извлекаются в случайном порядке: любой элемент такой структуры данных может быть выбран с равной вероятностью. Программа 18.11 представляет собой реализацию, которая обеспечивает такое поведение. Если использовать этот код для реализации АТД обобщенной очереди, то получится алгоритм случайного поиска на графе, где любая вершина, находящаяся в накопителе, с равной вероятностью может стать кандидатом на включение в дерево. Выбор ребра (ведущего в эту вершину) для добавления в дерево зависит от реализации операции обновить. Реализация в программе 18.11 не выполняет никаких обновлений, и каждая вершина из накопителя добавляется в дерево вместе с ребром, которое послужило причиной ее занесения в накопитель. Но можно, наоборот, выполнять все обновления (тогда в дерево будет добавляться самое последнее встреченное ребро из всех, которые ведут в каждую вершину, помещенную в накопитель), либо использовать случайный выбор.

Программа 18.11. Реализация рандомизированной очереди

При извлечении элемента из этой структуры данных с равной вероятностью выбирается любой из находящихся в ней элементов. Этот код можно использовать для реализации АТД обобщенной очереди для выполнения " случайного " поиска на графе (см. текст).

template <class Item>
class GQ
  { private:
      vector<Item> s; int N;
    public:
      GQ(int maxN) : s(maxN+1), N(0) { }
      int empty() const 
        { return N == 0; }
      void put(Item item)
        { s[N++] = item; }
      void update(Item x) { }
      Item get()
        { int i = int(N*rand()/(1.0+RAND MAX));
          Item t = s[i];
          s[i] = s[N-1];
          s[N-1] = t;
         return s[--N]; }
  };
      

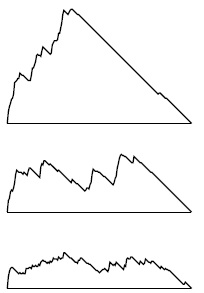
Рис. 18.28. Размеры накопителя при работе поиска в глубину, рандомизированного поиска и поиска в ширину

Эти графики размеров накопителя во время поисков, представленных на рис. 18.13, рис. 18.24 и рис. 18.29, показывают, какое огромное влияние оказывает на поиск на графе выбор структуры данных для накопителя. При использовании стека в DFS (вверху) накопитель заполняется в самом начале поиска, поскольку на каждом шаге мы находим новые узлы, а затем извлекаем из накопителя все его содержимое. При использовании рандомизированной очереди (в центре) максимальный размер очереди намного меньше. При использовании очереди FIFO в BFS (внизу) максимальный размер очереди еще меньше, а новые узлы обнаруживаются в процессе поиска.

Другая стратегия играет исключительно важную роль в изучении алгоритмов обработки графов, поскольку лежит в основе целого ряда классических алгоритмов, которые будут рассмотрены в лекциях 20—22 — это использование для накопителя АТД очереди с приоритетами (priority queue, см. "Очереди с приоритетами и пирамидальная сортировка" . Каждому ребру в накопителе присваивается определенное значение приоритета, которое затем может изменяться, и выбираем для очередного включения в дерево ребро с наивысшим приоритетом. Подробный анализ этого алгоритма будет проведен в главе 20 "Минимальные остовные деревья" . Операции по работе с очередью с приоритетами требуют больших затрат, чем аналогичные операции для стеков и очередей, поскольку для них необходимы неявные операции сравнения элементов очереди, но зато они могут поддерживать значительно более широкий класс алгоритмов поиска на графах. Как мы увидим ниже, некоторые из наиболее важных задач обработки графов можно решить, просто выбрав необходимый способ назначения приоритетов в реализации обобщенного поиска на графе на базе очереди с приоритетами.

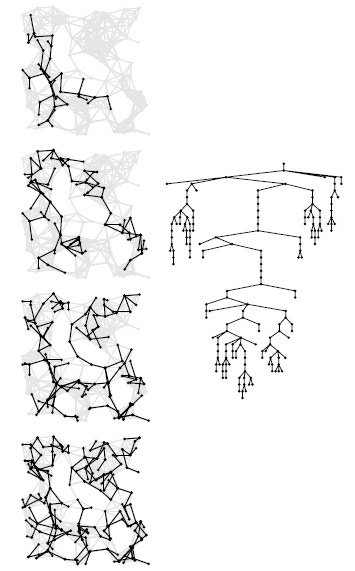
Все обобщенные алгоритмы поиска на графах просматривают каждое ребро всего один раз и в худшем случае требуют дополнительного объема памяти, пропорционального V; однако они все же различаются некоторыми показателями производительности. Например, на рис. 18.28 показано, как меняется размер накопителя в процессе выполнения поиска в глубину, в ширину и рандомизированного поиска; на рис. 18.29 показано дерево, вычисленное с помощью рандомизированного поиска для примера, представленного на рис. 18.13 и рис. 18.24. Для рандомизированного поиска не характерны ни длинные пути, как в DFS, ни узлы с большими степенями, как в BFS. Формы этих деревьев и графиков размеров накопителя зависят от структуры конкретного графа, на котором производится поиск, но они все-таки характеризуют различные алгоритмы.

Поиск на графах можно обобщить и далее, если работать с лесом (а не только с деревом). Мы уже вплотную пошли к этому уровню абстракции, однако отложим рассмотрение ряда таких алгоритмов до "Минимальные остовные деревья" .

Рис. 18.29. Граф рандомизированного поиска

Здесь показан процесс рандомизированного поиска на графе (слева) в том же стиле, что и на рисунках 18.13 и 18.24. Форма дерева поиска находится где-то между поиском в глубину и поиском в ширину. Динамические характеристики этих трех алгоритмов, которые отличаются только структурой данных, необходимой для выполнения работы, разительно отличаются.

Упражнения

18.61. Проанализируйте преимущества и недостатки реализации обобщенного поиска на графе на базе следующего правила: " Перенесите ребро из накопителя в дерево. Если вершина, в которую оно ведет, не посещалась, посетите эту вершину и занесите в накопитель все инцидентные ей ребра " .

18.62. Разработайте реализацию АТД графа, представленного списками смежности, которая содержит ребра (а не только их конечные вершины) в списках. Затем реализуйте поиск на графе, основанный на стратегии из упражнения 18.61, который посещает каждое ребро, но разрушает граф, воспользовавшись тем, что ребра всех вершин можно перемещать в накопитель с помощью изменения лишь одной ссылки.

18.63. Докажите, что рекурсивный поиск в глубину (программа 18.3) эквивалентен обобщенному поиску на графе с использованием стека (программа 18.10) в том смысле, что обе программы посещают все вершины любого графа в одном и том же порядке тогда и только тогда, когда эти программы просматривают списки смежности в разных направлениях.

18.64. Приведите три различных порядка обхода при рандомизированном поиске на графе

3-71-47-80-55-23-82-90-64-92-66-4.

18.65. Может ли рандомизированный поиск посетить вершины графа 3-7 1-4 7-8 0-5 5-2 3-8 2-9 0-6 4-9 2-6 6-4.

в порядке возрастания их индексов? Обоснуйте свой ответ.

18.66. Воспользуйтесь библиотекой STL для построения реализации обобщенной очереди ребер графа, которая блокирует занесение ребер с одинаковыми вершинами по правилу игнорирования новых элементов.

18.67. Разработайте алгоритм рандомизированного поиска на графе, который с равной вероятностью выбирает из накопителя любое ребро. Указание. См. программу 18.8.

18.68. Опишите стратегию обхода лабиринта, которая соответствует использованию обычного стека магазинного типа для обобщенного поиска на графе (см. раздел 18.1).

18.69. Добавьте в обобщенный поиск на графе (см. программу 18.10) возможность вывода значений высоты дерева и процента обработанных ребер для каждой просматриваемой вершины.

18.70. Эмпирически определите средние значения величин, описанных в упражнении 18.69, для обобщенного поиска на графе с использованием случайной очереди в графах различных размеров и построенных на основе различных моделей (см. упражнения 17.64—17.76).

18.71. Реализуйте производный класс, который строит динамические графические анимации обобщенного поиска на графах, в которых с каждой вершиной связаны координаты (x, у) (см. упражнения 17.55—17.59). Протестируйте полученную программу на случайных евклидовых графах с соседними связями, используя столько точек, сколько сможете обработать за приемлемый промежуток времени. Ваша программа должна строить изображения вроде диаграмм на рис. 18.13, рис. 18.24 и рис. 18.29, хотя для обозначения вершин и ребер, которые находятся в дереве, или в накопителе, или еще не просмотрены, вместо оттенков серого можно использовать различные цвета.