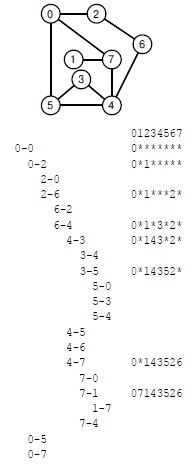Поиск на графе

Поиск в глубину

Метод Тремо интересен тем, что он непосредствен -но приводит к классическому рекурсивному методу обхода графов: посетив конкретную вершину, мы помечаем ее как посещенную, а затем рекурсивно посещаем все смежные с ней непомеченные вершины. Такой метод уже был кратко рассмотрен в "Элементарные структуры данных" и "Рекурсия и деревья" и использовался для решения задачи нахождения путей в "Виды графов и их свойства" — он называется поиск в глубину (DFS — depth-first search). Это один из наиболее важных алгоритмов из применяемых нами. Метод DFS с виду прост, поскольку основан на знакомой идее, и его нетрудно реализовать, но на самом деле это очень гибкий и мощный алгоритм, который можно применять для решения множества трудных задач обработки графов.

Программа 18.1 содержит класс DFS, который посещает все вершины и просматривает все ребра связного графа. Подобно функциям поиска простого пути, рассмотренным в "Виды графов и их свойства" , он основан на рекурсивной функции, которая использует приватный вектор для пометки пройденных вершин. В этой реализации используется вектор целых чисел ord, в котором сохраняется порядок посещения вершин. Трассировка на рис. 18.5 показывает, в каком порядке программа 18.1 обходит ребра и вершины, для примера, показанного на рис. 18.2 и рис. 18.3 (см. также рис. 18.17), при использовании реализации графа DenseGRAPH матрицей смежности из "Виды графов и их свойства" . На рис. 18.6 изображен процесс исследования лабиринта в виде стандартного чертежа графа.

Эти рисунки демонстрируют динамику рекурсивного DFS и его соответствие исследованию лабиринта методом Тремо. Во-первых, вектор, индексированный именами вершин, соответствует лампам на перекрестках: при обнаружении ребра, ведущего к уже посещенной вершине (т.е. в конце коридора виден свет), мы не выполняем рекурсивный вызов для прохода по этому ребру (т.е. как бы по коридору). Во-вторых, механизм вызова и возврата этой функции является аналогом нити в лабиринте: после обработки всех ребер, инцидентных некоторой вершине (исследуем все коридоры, отходящие от соответствующего перекрестка), мы возвращаемся (в обоих смыслах этого слова).

При обходе лабиринта каждый коридор встречается нам дважды, по одному разу с каждого конца. В графе каждое ребро также встречается дважды — по одному разу в каждой его вершине. При исследовании лабиринта методом Тремо мы открываем двери с обоих концов коридора. При поиске в глубину на неориентированном графе мы проверяем оба представления каждого ребра. Если мы встречаем ребро v-w, то либо выполняем рекурсивный вызов (если вершина w не помечена), либо пропускаем это ребро (если w помечена). Когда мы встретим это же ребро во второй раз, на этот раз как w-v, мы его игнорируем, поскольку вершину назначения v мы уже точно посещали (когда в первый раз встретились с этим ребром).

Программа 18.1. Поиск в глубину связного компонента

Класс DFS соответствует методу Тремо. Конструктор помечает как посещенные все вершины связного компонента, к которому принадлежит v; для этого он вызывает рекурсивную функцию searchC, которая посещает все вершины, смежные с v, проверяя их и вызывая себя для каждого ребра, которое ведет из v в непомеченную вершину. Клиенты могут воспользоваться функцией count для определения количества посещенных вершин и перегруженным оператором [] для определения последовательности посещения вершин алгоритмом.

  #include <vector>
  template <class Graph> class cDFS
    { int cnt;
      const Graph &G;
      vector <int> ord;
      void searchC(int v)
        { ord[v] = cnt++;
          typename Graph::adjIterator A(G, v);
          for (int t = A.beg(); !A.end(); t = A.nxt())
            if (ord[t] == -1) searchC(t);
        }
    public:
      cDFS(const Graph &G, int v = 0) :
        G(G), cnt(0), ord(G.V(), -1)
        { searchC(v); }
      int count() const { return cnt; }
      int operator[](int v) const { return ord[v]; }
    };
      

Рис. 18.5. Трасса работы DFS

Здесь показан порядок, в котором алгоритм поиска в глубину проверяет ребра и вершины в представлении матрицей смежности графа, изображенного на рис. 18.2 и рис. 18.3(вверху), и содержимое вектора ord (справа) при выполнении поиска (звездочки означают -1 для не посещенных вершин). Каждому ребру графа соответствуют две строки, по одной на каждое направление. Величина отступа определяет уровень рекурсии.

Рис. 18.6. Поиск в глубину

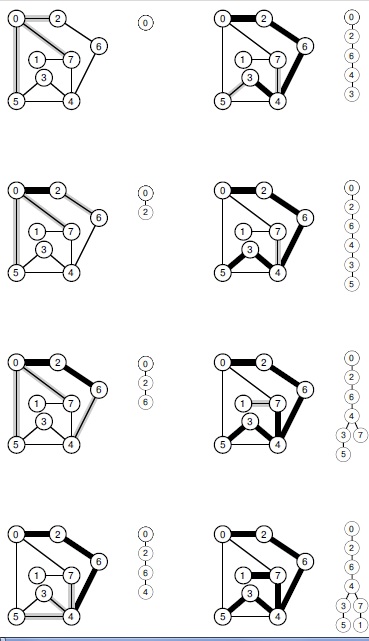
Данные диаграммы — графическое представление процесса, изображенного на рис. 18.5, в виде дерева рекурсивных вызовов при работе DFS. Ребра графа, выделенные жирными линиями, соответствуют ребрам в дереве DFS, показанном справа от каждой диаграммы. Ребра, выделенные серым — кандидаты на добавление в дерево на следующих шагах. На ранних стадиях (слева) дерево растет вниз в виде прямой линии, что соответствует рекурсивным вызовам для вершин 0, 2, 6 и 4. Затем выполняются рекурсивные вызовы для вершины 3, потом для вершины 5 (две верхних правых диаграммы), потом возврат из этих вызовов с последующими рекурсивными вызовами для вершины 7 из 4 (справа, вторая снизу) и для 1 из 7 (справа внизу).

Между поиском в глубину, реализованным в программе 18.1, и методом Тремо, изображенным на рис. 18.2 и рис. 18.3, имеется отличие, которое стоит рассмотреть, хотя во многих контекстах оно не играет никакой роли. При перемещении из вершины v в вершину w мы не проверяем элементы матрицы связности, которые соответствуют ребрам, ведущим из вершины w в другие вершины графа. В частности, мы знаем, что существует ребро из v в w, и оно будет проигнорировано, когда мы на него выйдем (поскольку v помечена как посещенная вершина). Это решение принимается в момент, отличный от решения в методе Тремо: там мы открываем дверь, соответствующую ребру из v в w, когда впервые переходим в вершину w из v. Если бы мы закрывали эти двери при входе и открывали при выходе (отметив коридор протянутой нитью), то тогда поиск в глубину точно соответствовал бы методу Тремо.

На рис. 18.6 показано дерево, соответствующее процессу рекурсивных вызовов на рис. 18.5. Это дерево рекурсивных вызовов, которое называется деревом DFS, представляет собой структурное описание процесса поиска. Как будет показано в разделе 18.4, слегка усовершенствованное дерево DFS может служить полным описанием не только структуры вызовов, но и динамики поиска.

Порядок обхода вершин зависит не только от графа, но и от его представления и реализации АТД. Например, на рис. 18.7 показана динамика поиска для реализации SparseMultiGRAPH списками смежности из "Виды графов и их свойства" . В случае представления матрицей смежности ребра, инцидентные каждой вершине, просматриваются в числовой последовательности. В случае же представления списками смежности они просматриваются в порядке, в котором занесены в список. Это различие приводит к совершенно другой динамике рекурсивного поиска. К аналогичному отличию приводит и последовательность ребер в списках (например, из-за построения одного и того же графа вставками ребер в различном порядке). Кстати, наличие параллельных ребер никак не влияет на поиск в глубину: любое ребро, параллельное уже пройденному ребру, игнорируется, поскольку его конечная вершина уже отмечена как посещенная.

Рис. 18.7. Трасса DFS (списки смежности)

Здесь показан порядок просмотра ребер и вершин при поиске в глубину на графе с рис. 18.5, представленном списками смежности.

Несмотря на все эти варианты, остается неизменным основное свойство алгоритма поиска в глубину: он посещает все ребра и все вершины, соединенные с исходной вершиной, независимо от порядка просмотра ребер, инцидентных каждой вершине. Это непосредственно следует из леммы 18.1, поскольку доказательство этой леммы не зависит от порядка открытия дверей на любом заданном перекрестке. Все изучаемые нами алгоритмы на основе DFS обладают этим очень важным свойством. Хотя динамика выполнения может существенно различаться в зависимости от представления графа и деталей реализации поиска, рекурсивная структура позволяет сделать правильные выводы о самом графе независимо от способа его представления и от порядка просмотра ребер, инцидентных каждой вершине.

Упражнения

18.4. Добавьте в программу 18.1 общедоступную функцию-член, которая возвращает размер связного компонента, просматриваемого конструктором.

18.5. Напишите клиентскую программу наподобие программы 17.6, которая просматривает граф, введенный из стандартного ввода, использует программу 18.1 для выполнения поиска из каждой вершины и выводит представление родительскими ссылками каждого остовного леса. Воспользуйтесь реализацией DenseGRAPH АТД графа из "Виды графов и их свойства" .

18.6. В стиле рис. 18.5 представьте трассу вызовов рекурсивной функции, выполненных при построении объекта DFS<DenseGRAPH для графа

0-20-51-23-44-53-5.

Начертите соответствующее дерево рекурсивных вызовов DFS.

18.7. В стиле рис. 18.6 продемонстрируйте процесс поиска для примера из упражнения 18.6.